Chamtivý algoritmus s příklady: chamtivá metoda a přístup

Chcete-li porozumět chamtivému přístupu, musíte mít pracovní znalosti o rekurzi a přepínání kontextu. To vám pomůže pochopit, jak sledovat kód. Chamtivé paradigma můžete definovat z hlediska vlastních nezbytných a dostatečných prohlášení.

dvě podmínky definují chamtivé paradigma.

• každé postupné řešení musí strukturovat problém směrem k jeho nejlépe přijatému řešení.
• postačí, když se strukturování problému může zastavit v konečném počtu chamtivých kroků.

s pokračováním teoretizace popíšeme historii spojenou s chamtivým vyhledávacím přístupem.

V tomto Chamtivý algoritmus tutorial, budete:

• Historie Greedy Algoritmy
• Greedy Strategie a Rozhodnutí
• Vlastnosti Chamtivý Přístup
• Proč používat Chamtivý Přístup?
• Jak Vyřešit činnost výběrové problém
• Architektura Chamtivý přístup
• Nevýhody Greedy Algoritmy

Historie Greedy Algoritmy

Tady je důležitý mezník greedy algoritmy:

• Greedy algoritmy byly vymyšleny pro mnohé graf chodit algoritmy v roce 1950.
• Esdger Djikstra koncipován algoritmus pro generování minimální kostry stromů. Jeho cílem bylo zkrátit rozpětí tras v nizozemském hlavním městě Amsterdamu.
• ve stejném desetiletí dosáhli Prim a Kruskal optimalizačních strategií, které byly založeny na minimalizaci nákladů na cestu po vážených trasách.
• v 70. letech navrhli Američtí vědci, Cormen, Rivest a Stein rekurzivní substrukturu chamtivých řešení ve své klasické knize úvod do algoritmů.
• paradigma chamtivého vyhledávání bylo zaregistrováno jako jiný typ optimalizační strategie v záznamech NIST v roce 2005.
• protokoly, které provozují web, jako je open-shortest-path-first (OSPF) a mnoho dalších protokolů pro přepínání síťových paketů, používají chamtivou strategii k minimalizaci času stráveného v síti.

Greedy Strategie a Rozhodnutí

Logika ve své nejjednodušší formě byla scvrkla na „chamtivý“ nebo „ne chamtivý“. Tato tvrzení byla definována přístupem přijatým k postupu v každé fázi algoritmu.

například algoritmus Djikstry využil postupnou chamtivou strategii identifikace hostitelů na internetu výpočtem nákladové funkce. Hodnota vrácená funkcí nákladů určila, zda je další cesta „chamtivá“ nebo „nenažraná“.

Stručně řečeno, algoritmus přestává být chamtivý, pokud v jakékoli fázi podnikne krok, který není lokálně chamtivý. Chamtivé problémy se zastavují bez dalšího rozsahu chamtivosti.

Vlastnosti Chamtivý Přístup

důležité vlastnosti Chamtivý metoda, algoritmus, jsou:

• je to uspořádaný seznam zdrojů, s náklady nebo hodnota pravomocí. Tyto kvantifikovat omezení na systému.
• budete mít maximální množství zdrojů v době omezení platí.
• například v problému plánování aktivit jsou náklady na zdroje v hodinách a činnosti je třeba provádět v sériovém pořadí.

Proč používat chamtivý přístup?

Zde jsou důvody pro použití greedy přístup:

• chamtivý přístup má několik kompromisů, které může být vhodný pro optimalizaci.
• jedním z významných důvodů je okamžité dosažení co nejschůdnějšího řešení. V problému výběru aktivity (vysvětleno níže), pokud lze před dokončením aktuální aktivity provést více činností, lze tyto činnosti provést ve stejnou dobu.
• dalším důvodem je rozdělení problému rekurzivně na základě podmínky, bez nutnosti kombinovat všechna řešení.
• v problému výběru aktivity je krok „rekurzivní dělení“ dosažen skenováním seznamu položek pouze jednou a zvážením určitých činností.

jak vyřešit problém s výběrem aktivity

v příkladu plánování aktivity je pro každou aktivitu čas „start“ a „dokončit“. Každá aktivita je indexována číslem pro referenci. Existují dvě kategorie aktivit.

1. uvažovaná aktivita: je aktivita, která je odkazem, ze kterého je analyzována schopnost provádět více než jednu zbývající aktivitu.
2. zbývající činnosti: činnosti na jednom nebo více indexech před uvažovanou činností.

celková doba trvání udává náklady na provedení činnosti. To znamená, že (finish – start) nám dává trvání jako náklady na činnost.

dozvíte se, že chamtivý rozsah je počet zbývajících činností, které můžete provést v době uvažované činnosti.

Architektura Chamtivý přístup

KROK 1)

Skenování seznam náklady činnosti, počínaje index 0 jako za Index.

Krok 2)

když lze do té doby dokončit více aktivit, uvažovaná aktivita skončí, začněte hledat jednu nebo více zbývajících aktivit.

Krok 3)

pokud již nejsou zbývající aktivity, stává se současná zbývající aktivita další uvažovanou aktivitou. Opakujte krok 1 a krok 2 s novou uvažovanou aktivitou. Pokud zbývají žádné další aktivity, přejděte ke kroku 4.

Krok 4)

vraťte spojení uvažovaných indexů. Jedná se o indexy aktivity, které budou použity k maximalizaci propustnosti.

Kód Vysvětlení

#include<iostream>#include<stdio.h>#include<stdlib.h>#define MAX_ACTIVITIES 12

Vysvětlení kódu:

1. Součástí záhlaví souborů/tříd
2. maximální počet činností, které uživatel poskytl.

using namespace std;class TIME{ public: int hours; public: TIME() { hours = 0; }};

vysvětlení kódu:

1. jmenný prostor pro streamování operací.
2. a class definition for TIME
3. an hour timestamp.
4. výchozí konstruktor času
5. proměnná hodin.

class Activity{ public: int index; TIME start; TIME finish; public: Activity() { start = finish = TIME(); }};

Vysvětlení kódu:

1. definice třídy z činnosti
2. časové razítko vymezující dobu trvání
3. Všechny časové údaje jsou inicializován na 0 ve výchozím konstruktor

class Scheduler{ public: int considered_index,init_index; Activity *current_activities = new Activity; Activity *scheduled;

Vysvětlení kódu:

1. Část 1 plánovače definice třídy.
2. uvažovaný Index je výchozím bodem pro skenování pole.
3. Inicializační index se používá k přiřazení náhodných časových razítek.
4. pole objektů aktivity je dynamicky přiděleno pomocí nového operátora.
5. plánovaný ukazatel definuje aktuální umístění základny pro chamtivost.

Scheduler(){ considered_index = 0; scheduled = NULL;......

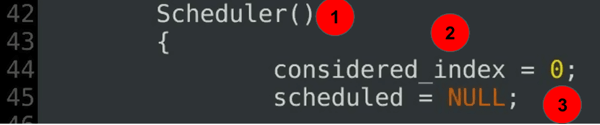
Vysvětlení kódu:

1. plánovač, konstruktér – část 2 plánovače definice třídy.
2. uvažovaný index definuje aktuální začátek aktuálního skenování.
3. aktuální chamtivý rozsah je na začátku nedefinován.

for(init_index = 0; init_index < MAX_ACTIVITIES; init_index++) { current_activities.start.hours = rand() % 12; current_activities.finish.hours = current_activities.start.hours + (rand() % 2); printf("\nSTART:%d END %d\n", current_activities.start.hours ,current_activities.finish.hours); }……

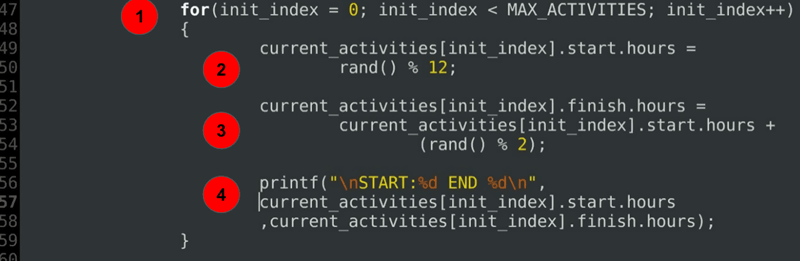
vysvětlení kódu:

1. smyčka pro inicializaci počátečních a koncových hodin každé z aktuálně naplánovaných činností.
2. inicializace počátečního času.
3. inicializace času ukončení vždy po nebo přesně v počáteční hodině.
4. příkaz ladění vytisknout přidělené doby trvání.

public: Activity * activity_select(int);};

Vysvětlení kódu:

1. 4. Část – poslední část plánovače definice třídy.
2. funkce Activity select bere jako základnu index výchozího bodu a rozděluje chamtivý úkol na chamtivé dílčí problémy.

Activity * Scheduler :: activity_select(int considered_index){ this->considered_index = considered_index; int greedy_extent = this->considered_index + 1;…… 

1. pomocí operátoru rozlišení rozsahu (::) je poskytnuta definice funkce.
2. uvažovaný Index je Index nazvaný hodnotou. Greedy_extent je inicializovaný jen index po uvažovaném indexu.

Activity * Scheduler :: activity_select(int considered_index){ while( (greedy_extent < MAX_ACTIVITIES ) && ((this->current_activities).start.hours < (this->current_activities).finish.hours )) { printf("\nSchedule start:%d \nfinish%d\n activity:%d\n", (this->current_activities).start.hours, (this->current_activities).finish.hours, greedy_extent + 1); greedy_extent++; }…...

Vysvětlení kódu:

1. základní logika – chamtivý rozsah je omezen na množství aktivit.
2. počáteční hodiny aktuální aktivity se kontrolují jako plánovatelné před tím, než by uvažovaná aktivita (daná uvažovaným indexem) skončila.
3. pokud je to možné, vytiskne se volitelný příkaz ladění.
4. Postoupit do další index na pole činnosti

...if ( greedy_extent <= MAX_ACTIVITIES ) { return activity_select(greedy_extent); } else { return NULL; }}

Vysvětlení kódu:

1. podmíněné zkontroluje, zda všechny činnosti byly pokryty.
2. pokud ne, můžete restartovat chamtivý s uvažovaným indexem jako aktuálním bodem. Jedná se o rekurzivní krok, který lačně rozděluje problémové prohlášení.
3. pokud ano, vrátí se volajícímu bez prostoru pro rozšíření chamtivosti.

int main(){ Scheduler *activity_sched = new Scheduler(); activity_sched->scheduled = activity_sched->activity_select( activity_sched->considered_index); return 0;}

Vysvětlení kódu:

1. hlavní funkce použity k vyvolat plánovač.
2. nový plánovač je instance.
3. funkce activity select, která vrací ukazatel typu activity, se vrátí volajícímu po skončení chamtivého hledání.

Výstup:

START:7 END 7START:9 END 10START:5 END 6START:10 END 10START:9 END 10Schedule start:5 finish6 activity:3Schedule start:9 finish10 activity:5

Nevýhody Greedy Algoritmy

není vhodný pro Chamtivý problémy, kde řešení je nutné pro každý trápím jako třídění.

v takových chamtivých algoritmických praktických problémech může být chamtivá metoda špatná; v nejhorším případě dokonce vést k neoptimálnímu řešení.

nevýhodou chamtivých algoritmů je proto, že nevědí, co leží před současným chamtivým stavem.

Níže je vyobrazení nevýhodou Greedy metoda:

V chamtivý scan zde zobrazen jako strom (vyšší hodnota vyšší, chamtivost), algoritmus státu v hodnotě: 40, je pravděpodobné, že se 29 jako další hodnotu. Dále jeho pátrání končí ve 12. To činí hodnotu 41.

Nicméně, pokud algoritmus vzal suboptimální cestu nebo přijal strategii dobývání. po 25 by následovalo 40 a celkové zlepšení nákladů by bylo 65, což je o 24 bodů vyšší jako neoptimální rozhodnutí.

příklady chamtivých algoritmů

většina síťových algoritmů používá chamtivý přístup. Zde je seznam několika příkladů chamtivých algoritmů:

• Prim Minimal Spanning Tree Algoritmus
• Problém obchodního Cestujícího
• Graf – Mapa Zbarvení
• Kruskal je Minimální Spanning Tree Algoritmus
• Dijkstra je Minimální Spanning Tree Algoritmus
• Graf – Vertex Cover
• Problém Batohu
• Plánování Práce Problém

Shrnutí:

Chcete-li shrnout, článek definovanými chamtivý paradigma, ukázal, jak chamtivý optimalizace a rekurze, vám může pomoci získat nejlepší řešení, a to až do bodu. Greedy algoritmus je široce přijata do aplikace pro řešení problémů v mnoha jazycích jako Greedy algoritmus Python, C, C#, PHP, Java, atd. Příklad výběru aktivity Greedy algorithm byl popsán jako strategický problém, který by mohl dosáhnout maximální propustnosti pomocí greedy přístupu. Nakonec byly vysvětleny nedostatky používání chamtivého přístupu.