Najít optimální řešení pro určité optimalizační problémy mohou být neuvěřitelně obtížný úkol, často prakticky nemožné. Je to proto, že když se problém dostane dostatečně velký, musíme hledat obrovské množství možných řešení, abychom našli optimální řešení. I při moderním výpočetním výkonu je stále příliš mnoho možných řešení, která je třeba zvážit. V tomto případě, protože nemůžeme reálně očekávat, že najdeme optimální v rozumné době, musíme se spokojit s něčím, co je dostatečně blízko.
příkladem optimalizačního problému, který má obvykle velké množství možných řešení, by byl problém obchodního cestujícího. Abychom našli řešení problému, jako je problém obchodního cestujícího, musíme použít algoritmus, který dokáže najít dostatečně dobré řešení v rozumném čase. V předchozím tutoriálu jsme se podívali na to, jak bychom to mohli udělat s genetickými algoritmy, a i když genetické algoritmy jsou jeden způsob, jak můžeme najít ‚dost dobrý‘ řešení pro problém obchodního cestujícího, tam jsou další jednodušší algoritmy můžeme realizovat, že bude také nám najít téměř optimální řešení. V tomto tutoriálu je algoritmus, který budeme používat, „simulované žíhání“.
pokud nejste obeznámeni s problémem obchodního cestujícího, mohlo by se stát, že se před pokračováním podíváte na můj předchozí tutoriál.
co je simulované žíhání?
nejprve se podívejme na to, jak simulované žíhání funguje a proč je dobré najít řešení zejména problému obchodního cestujícího. Simulovaný algoritmus žíhání byl původně inspirován procesem žíhání v kovoobrábění. Žíhání zahrnuje zahřívání a chlazení materiálu, aby se změnily jeho fyzikální vlastnosti v důsledku změn jeho vnitřní struktury. Jak se kov ochladí, jeho nová struktura se stává pevnou, což způsobuje, že si kov zachová své nově získané vlastnosti. V simulovaném žíhání udržujeme teplotní proměnnou, která simuluje tento proces ohřevu. Zpočátku jsme jej nastavili vysoko a poté jej nechali pomalu „vychladnout“ při spuštění algoritmu. I když je tato teplotní proměnná vysoká, algoritmus bude moci s větší frekvencí přijímat řešení, která jsou horší než naše současné řešení. To dává algoritmu schopnost vyskočit z jakýchkoli lokálních optimum, které se ocitne na začátku provádění. Protože teplota je snížena, takže je pravděpodobnost přijetí horšího řešení, a proto umožňuje algoritmus postupně zaměřit na oblasti hledání prostoru, v němž, doufejme, v blízkosti lze najít optimální řešení. Tento postupný proces „chlazení“ je to, co dělá simulovaný algoritmus žíhání pozoruhodně efektivní při hledání téměř optimálního řešení při řešení velkých problémů, které obsahují četné lokální optimum. Povaha problému obchodního cestujícího z něj dělá dokonalý příklad.
Výhody Simulované Žíhání
můžete se zeptat, jestli existuje nějaká skutečná výhoda pro provádění simulovaného žíhání přes něco jako jednoduchý kopec horolezec. Ačkoli horolezci mohou být překvapivě efektivní při hledání dobrého řešení, mají také tendenci uvíznout v místních optimums. Jak jsme již dříve zjistili, simulovaný algoritmus žíhání je vynikající při vyhýbání se tomuto problému a v průměru je mnohem lepší při hledání přibližného globálního Optima.
abychom lépe porozuměli, pojďme se rychle podívat na to, proč je základní algoritmus horolezectví tak náchylný k zachycení v místních optimumech.
algoritmus horolezce jednoduše přijme řešení sousedů, která jsou lepší než současné řešení. Když horolezec nemůže najít lepší sousedy, zastaví se.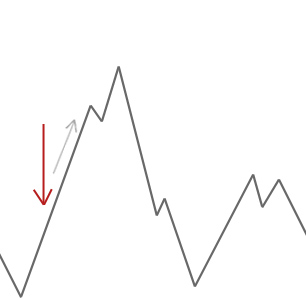
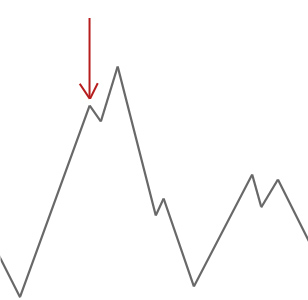
V příkladu výše jsme začít náš kopec horolezec na červenou šipku a pracuje jeho cestu nahoru do kopce, až dosáhne bodu, kde to nemůže vyšplhat výš, aniž by nejprve sestupně. V tomto příkladu můžeme jasně vidět, že se zasekl v místním optimu. Pokud by se jednalo o skutečný světový problém, nevěděli bychom, jak vyhledávací prostor vypadá, takže bychom bohužel nebyli schopni říci, zda je toto řešení někde blízko globálního optimu.
simulované žíhání funguje trochu jinak než toto a občas přijme horší řešení. Tato charakteristika simulovaného žíhání pomáhá vyskočit z místní optima může mít jinak uvízli.
akceptační funkce
pojďme se podívat na to, jak algoritmus rozhoduje, která řešení přijmout, abychom lépe porozuměli tomu, jak se těmto lokálním optimům vyhnout.
nejprve zkontrolujeme, zda je řešení sousedů lepší než naše současné řešení. Pokud ano, přijímáme to bezpodmínečně. Pokud však řešení sousedů není lepší, musíme zvážit několik faktorů. Za prvé, o kolik horší je řešení sousedů; a za druhé, jak vysoká je současná „teplota“ našeho systému. Při vysokých teplotách je systém s větší pravděpodobností přijímat řešení, která jsou horší.
matematika pro to je docela jednoduché:
v Podstatě, čím menší je změna energie (kvalitu řešení), a čím vyšší je teplota, tím více je pravděpodobné, že pro algoritmus přijmout řešení.
přehled algoritmů
jak tedy algoritmus vypadá? Ve své nejzákladnější implementaci je to docela jednoduché.
- nejprve musíme nastavit počáteční teplotu a vytvořit náhodné počáteční řešení.
- pak začneme opakovat, dokud nebude splněna naše podmínka zastavení. Obvykle se buď systém dostatečně ochladil, nebo bylo nalezeno dostatečné řešení.
- odtud vybereme souseda malou změnou našeho současného řešení.
- pak se rozhodneme, zda se přestěhujeme do tohoto sousedního řešení.
- a Konečně, musíme snížit teplotu a pokračovat v opakování
Teplota Inicializace
Pro lepší optimalizaci, při inicializaci proměnná teplota bychom měli vybrat teplotu, která bude zpočátku umožňují prakticky jakýkoli krok proti současnému řešení. To dává algoritmu schopnost lépe prozkoumat celý vyhledávací prostor před ochlazením a usazením ve více zaměřené oblasti.
příkladový kód
nyní použijme to, co víme, k vytvoření základního simulovaného algoritmu žíhání, a poté jej aplikujte na níže uvedený problém cestovního prodavače. V tomto tutoriálu budeme používat Javu, ale logika by snad měla být dostatečně jednoduchá, aby mohla Kopírovat do libovolného jazyka podle vašeho výběru.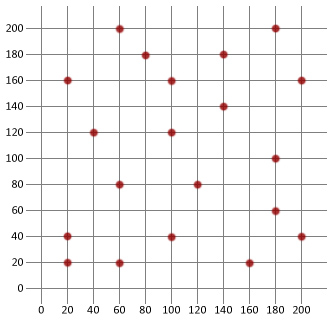
Nejprve musíme vytvořit Městské třídy, které mohou být použity k modelování různých destinací naší obchodní cestující.
Město.java
* Město.java
* Models a city
* /
package sa;
public class City {
int x;
int y;
/ / vytváří náhodně umístěné město
veřejné Město () {
toto.x = (int)(Math.random () * 200);
toto.y = (int)(Math.random()*200);
}
// vytvoří město na zvoleném místě x, y
veřejné Město (int x, int y){
toto.x = x;
toto.y = y;
}
// Gets city ‚ s X coordinate
public int getX () {
vraťte to.x;
}
// dostane městské souřadnice y
veřejné int getY () {
vraťte to.y;
}
// dostane vzdálenost k danému městu
veřejné dvojité distanceTo (City city){
int xDistance = Math.abs (getX () – město.getX());
int yDistance = Math.abs(getY () – město.getY ());
double distance = Math.sqrt( (xDistance*xDistance) + (yDistance*yDistance) );
návrat vzdálenosti;
}
@Override
veřejnost String toString(){
návrat getX()+“, „+getY();
}
}
Další pojďme vytvořit třídu, která lze sledovat z měst.
TourManager.java
* TourManager.java
* drží města turné
* /
package sa;
import java.util.ArrayList;
public class TourManager {
// Má naše města
private static ArrayList destinationCities = new ArrayList<Město>();
// Přidá cílové město
public static void addCity(Město město) {
destinationCities.add(město);
}
// získejte město
veřejné statické Město getCity (int index){
návrat (Město)destinationCities.get(index);
}
// Získat číslo destinace měst
public static int numberOfCities(){
návrat destinationCities.velikost();
}
}
nyní vytvořit třídu, která může modelovat cestovní prodavač turné.
prohlídka.java
* prohlídka.java
* ukládá kandidátskou prohlídku ve všech městech
* /
package sa;
import java.util.ArrayList;
import java.util.Sbírek;
public class Turné{
// Drží naši prohlídku města
private ArrayList tour = new ArrayList<Město>();
// Cache
private int vzdálenost = 0;
// Vytvoří prázdný tour
veřejné Tour(){
for (int i = 0; i < TourManager.numberOfCities (); i++) {
tour.přidat (null);
}
}
// konstruuje turné z jiného turné
veřejné turné (ArrayList tour){
toto.tour = (ArrayList) tour.klon();
}
// Vrátí turistické informace
public ArrayList getTour(){
návrat turné;
}
// Vytváří náhodné individuální
veřejnost void generateIndividual() {
// Smyčka přes všechny naše destinace měst a přidat je do našeho turné
for (int cityIndex = 0; cityIndex < TourManager.numberOfCities (); cityIndex++) {
setCity (cityIndex, TourManager.getCity (cityIndex));
}
// náhodně změnit pořadí turné
sbírky.shuffle (prohlídka);
}
/ / získá město z prohlídky
veřejné město getCity (int tourPosition) {
návrat (City)tour.get (tourPosition);
}
// nastaví město na určitou pozici v rámci prohlídky
public void setCity (int tourPosition, City city) {
tour.set(tourPosition, město);
// v Případě, že výlety byly změněny musíme obnovit fitness a vzdálenost
vzdálenost = 0;
}
// Dostane celková vzdálenost turné
public int getDistance(){
, pokud (vzdálenost == 0) {
int tourDistance = 0;
// Smyčka přes naše prohlídka města
for (int cityIndex=0; cityIndex < tourSize(); cityIndex++) {
// Získat město cestujeme z
Město fromCity = getCity(cityIndex);
// Město cestujeme
Město destinationCity;
// Zkontrolujte, zda nejsme na naše turné je poslední město, když jsme si stanovili naše
// tour final destination města do města
, pokud(cityIndex+1 < tourSize()){
destinationCity = getCity(cityIndex+1);
}
else{
destinationCity = getCity(0);
}
// Získat vzdálenosti mezi dvěma městy
tourDistance += fromCity.distanceTo (destinationCity);
}
distance = tourDistance;
}
zpáteční vzdálenost;
}
// získejte počet měst na našem turné
public int tourSize() {
return tour.velikost();
}
@Přepsat
veřejnost String toString() {
String geneString = „|“;
for (int i = 0; i < tourSize(); i++) {
geneString += getCity(já)+“|“;
}
návrat geneString;
}
}
Konečně, pojďme vytvořit naši simulované žíhání algoritmus.
simulováno.java
public class SimulatedAnnealing {
// Vypočítat pravděpodobnost přijetí
public static double acceptanceProbability(int energie, int newEnergy, dvojí teplota) {
//, Pokud nové řešení je lepší, přijmout
, pokud (newEnergy < energie) {
návrat 1.0;
}
// Pokud nové řešení je horší, vypočítat pravděpodobnost přijetí
return Math.exp((energie – newEnergy) / teplota);
}
public static void main(String args) {
// Vytvořit a přidat naše města
Města = nové Město(60, 200);
TourManager.addCity (město);
City city2 = Nové Město (180, 200);
TourManager.addCity (city2);
City city3 = Nové Město(80, 180);
TourManager.addCity (city3);
City city4 = Nové Město(140, 180);
TourManager.addCity (city4);
City city5 = Nové Město(20, 160);
TourManager.addCity (city5);
City city6 = Nové Město(100, 160);
TourManager.addCity (city6);
City city7 = Nové Město(200, 160);
TourManager.addCity (city7);
City city8 = Nové Město(140, 140);
TourManager.addCity (city8);
City city9 = Nové Město(40, 120);
TourManager.addCity (city9);
City city10 = Nové Město (100, 120);
TourManager.addCity (city10);
City city11 = Nové Město(180, 100);
TourManager.addCity (city11);
City city12 = Nové Město(60, 80);
TourManager.addCity (city12);
City city13 = Nové Město(120, 80);
TourManager.addCity (city13);
City city14 = Nové Město(180, 60);
TourManager.addCity (city14);
City city15 = Nové Město(20, 40);
TourManager.addCity (city15);
City city16 = Nové Město(100, 40);
TourManager.addCity (city16);
City city17 = Nové Město(200, 40);
TourManager.addCity (město17);
City city18 = Nové Město (20, 20);
TourManager.addCity (city18);
City city19 = Nové Město(60, 20);
TourManager.addCity (city19);
City city20 = Nové Město(160, 20);
TourManager.addCity(city20);
// Nastavit počáteční teplota
double temp = 10000;
// rychlost Chlazení
double coolingRate = 0.003;
// Inicializace vstupního roztoku
Tour currentSolution = new Tour();
currentSolution.generateIndividual ();
systém.mimo.println („počáteční vzdálenost řešení:“ + currentSolution.getDistance());
// Nastavit jako aktuální nejlepší
Tour best = new Tour (currentSolution.getTour());
// Loop dokud se systém ochladí
zatímco (temp > 1) {
// Vytvořit nový soused tour
Tour newSolution = new Tour(currentSolution.getTour ());
// získejte náhodné pozice v turné
int tourPos1 = (int) (newSolution.tourSize () * Math.random());
int tourPos2 = (int) (newSolution.tourSize () * Math.random());
/ / získejte města na vybraných pozicích v prohlídce
City citySwap1 = newSolution.getCity (tourPos1);
City citySwap2 = newSolution.getCity (tourPos2);
/ / zaměňte je
newSolution.setCity (tourPos2, citySwap1);
newSolution.setCity (tourPos1, citySwap2);
/ / získejte energii řešení
int currentEnergy = currentSolution.getDistance ();
int neighbourEnergy = newSolution.getDistance ();
// rozhodněte se, zda bychom měli přijmout souseda
if (acceptanceProbability (currentEnergy, neighbourEnergy, temp) > Math.random()) {
currentSolution = nová prohlídka (newSolution.getTour());
}
// Sledujte nejlepší nalezené řešení
if (currentSolution.getDistance () < nejlepší.getDistance()) {
best = new Tour (currentSolution.getTour());
}
// Cool system
temp * = 1-coolingRate;
}
systém.mimo.println („konečné řešení vzdálenost:“ + nejlepší.getDistance ());
systém.mimo.system. out. println(„Turné:“ + nejlepší);
}
}
Výstup
Konečné řešení vzdálenost: 911
Tour: |180, 200/200, 160/140, 140/180, 100/180, 60/200, 40/160, 20/120, 80/100, 40/60, 20/20, 20/20, 40/60, 80/100, 120/40, 120/20, 160/60, 200/80, 180/100, 160/140, 180|
Závěr
V tomto příkladu jsme byli schopni více než polovina vzdálenosti naše původní náhodně generované trase. To snad ukazuje, jak šikovný je tento relativně jednoduchý algoritmus při použití na určité typy optimalizačních problémů.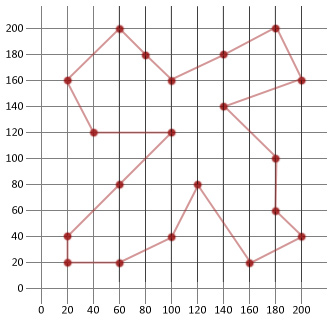
Autor
 Dobrý den, jsem Lee.
Dobrý den, jsem Lee.jsem vývojář z Velké Británie, který miluje technologie a podnikání. Zde najdete články a návody o věcech, které mě zajímají. Pokud si mě chcete najmout nebo se o mně dozvědět více, přejděte na stránku o mně