začal jsem dělat populární kurz strojového učení Andrewa Ng na Coursera. První týden pokrývá hodně, alespoň pro někoho, kdo se nedotkl mnohem kalkul na pár let
- Nákladové Funkce (průměrný rozdíl na druhou)
- Gradient Sestupu
- Lineární Regrese
Těchto tří témat bylo hodně. Budu mluvit o každém podrobně, a jak se všichni do sebe zapadají, s nějakým pythonovým kódem k prokázání.
upravit 4. května: Publikoval jsem sledování se zaměřením na to, jak zde funguje nákladová funkce, včetně intuice, jak ji vypočítat ručně a dvou různých implementací Pythonu. Můžu udělat gradientní sestup a pak je spojit pro lineární regresi brzy.
Model Reprezentace
za Prvé, cílem většiny algoritmů strojového učení je vytvořit model hypotézu, která může být použita pro odhad Y na základě X. hypotéza, nebo model, mapy vstupů na výstupy. Řekněme například, že trénuji model založený na spoustě údajů o bydlení, které zahrnují velikost domu a prodejní cenu. Školením modelu, mohu vám odhadnout, za kolik můžete prodat svůj dům na základě jeho velikosti. Toto je příklad regresního problému-vzhledem k nějakému vstupu chceme předpovědět spojitý výstup.
hypotéza je obvykle prezentován jako

theta hodnoty jsou parametry.
příklady, jak můžeme vizualizovat hypotéza:
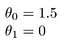
Tato výnosy h(x) = 1.5 + 0x. 0x znamená žádný sklon a y bude vždy konstanta 1,5. Vypadá to jako:

Jak o
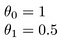

cílem vytvoření modelu je zvolit parametry, nebo hodnoty theta, tak, že h(x) se blíží k y pro přípravu dat, x a y. Takže pro tato data
x =
y =

budu se snažit a najít nejlepší fit pomocí lineární regrese. Tak začneme.
nákladová funkce
potřebujeme funkci, která minimalizuje parametry nad naší datovou sadou. Jednu společnou funkci, která je často používán je střední čtvercová chyba, které měří rozdíl mezi odhad (dataset) a odhadované hodnoty (předpověď). Vypadá to takto:

ukázalo se, Že můžeme upravit rovnice trochu, aby se výpočet po trati trochu víc jednoduché. Jsme se nakonec s:
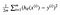
Pojďme použít const, funkce pro sledování dat:

Pro teď budeme počítat některé hodnoty theta a spiknutí nákladové funkce ručně. Protože tato funkce prochází (0, 0), díváme se pouze na jednu hodnotu theta. Od této chvíle budu označovat funkci nákladů jako J (Θ).
pro J (1)dostaneme 0. Žádné překvapení-hodnota J (1) poskytuje přímku, která dokonale odpovídá datům. A co J(0,5)?

MSE funkce nám dává hodnotu 0,58. Zakresleme obě dosavadní hodnoty:
J(1) = 0
J (0,5) = 0.58

budu pokračovat a vypočítat některé další hodnoty J(Θ).

A když jsme se připojit tečky dohromady pěkně…

můžeme vidět, že nákladová funkce je na minimum, když se theta = 1. To dává smysl – naše počáteční data jsou přímka se sklonem 1 (oranžová čára na obrázku výše).
Gradient Sestupu
minimalizovat J(Θ) metodou pokusů a omylů výše — jen se snažím spoustu hodnot a vizuálně kontrolu výsledného grafu. Musí existovat lepší způsob? Sestup přechodu fronty. Gradient Descent je obecná funkce pro minimalizaci funkce, v tomto případě funkce střední kvadratické chyby.
Gradient Sestupu v podstatě jen dělá to, co jsme dělali ručně — změna theta hodnoty nebo parametry, kousek po kousku, dokud jsme snad dorazili minimum.
začneme inicializací theta0 a theta1 na libovolné dvě hodnoty, řekněme 0 pro obě, a odtud. Formálně, algoritmus je následující:

kde α, alfa, je rychlost učení, nebo jak rychle se chceme pohybovat směrem k minimální. Pokud je α příliš velké, můžeme to přehnat.

Přináší to všechno dohromady — Lineární Regrese
Rychle shrneme-li:
Máme hypotézu:

které potřebujeme, aby se vešly naše tréninková data. Můžeme použít nákladovou funkci, jako je střední kvadratická chyba:

které můžeme minimalizovat použitím gradientní sestup:

Což nás vede k naší první strojového učení algoritmus, lineární regrese. Poslední část skládačky, kterou musíme vyřešit, abychom měli funkční lineární regresní model, je částečný derivát nákladové funkce:
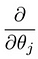
Který se ukáže být:
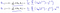
Což nám dává lineární regresní!
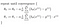
S teorií z cesty, půjdu dál realizovat tuto logiku v pythonu v příštím příspěvku.
Upravit 4. Května: publikoval jsem sledovat se zaměřením na to, jak Stát funguje, včetně intuici, jak to spočítat ručně a dvě různé implementace Python. Můžu udělat gradientní sestup a pak je spojit pro lineární regresi brzy.