TEPELNÁ VODIVOST

Tepelná vodivost pevných látek je odlišné povahy v závislosti na tom, zda jsou nebo nejsou vodiče. V dielektrikách bez volných elektrických nábojů je tepelná energie přenášena fonony. Kolektivní vibrace atomů v krystalové mřížce mají podobu posunovacích vln, jejichž interference generuje vlnové pakety, tj. Posunutí vlny způsobují kolísání hustoty, které se mohou projevit jako variace indexu lomu. Pokud vlny procházejí oblastí, ve které se index lomu liší od střední objemové hodnoty, budou následné posunovací vlny nesoucí energii tepelného pohybu rozptýleny.

rozptyl je silnější, tím větší je maximální odchylka atomů od jejich středních poloh v mřížce, tj. To představuje experimentálně prokázaným faktem, že tepelná vodivost krystalů dielektrika snižuje na poměrně vysoké teploty: λ1/T (Obrázek 1).

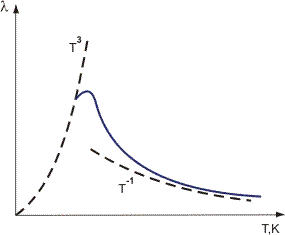
Obrázek 1. Změna tepelné vodivosti krystalových dielektrik s teplotou.

Debye dal nahlédnout do vrcholného charakteru λ (T) variace při nízkém T v rámci kvantově mechanických konceptů. Vypracoval dipólovou teorii dielektrik založenou na konceptu molekuly jako tuhého dipólu. V tomto modelu Debye představil koncept tzv. Debyeovy teploty úměrné maximální frekvenci atomových vibrací v pevné látce. Pro většinu látek θD je buď nižší než nebo blízko pokojové teplotě (výjimkou je diamant, pro který θD = 1850 K a berrylium, pro které θD = 1160K).

V kvantové teorii pevných látek, krystalová mřížka je považován za objem naplněné s phonon plynu, který odpočet z nejjednodušších kinetické teorie je aplikovaná

kde c je tepelná kapacita a dielektrická, že se shoduje s phonon plynu, v je průměrná rychlost fonony přibližně stejná jako rychlost zvuku,střední volná dráha fonony. Existence určité konečné hodnotyje výsledkem phonon rozptyl na fonony, na vady krystalové mřížky, a zejména na hranicích zrn přes celý vzorek. Teplotní závislost λ(T) je určena hodnotoua c na teplotě.

Při vysokých teplotách podstatně vyšší než Debye teplota θD, základní mechanismus omezeníje phonon-fononové rozptyl v důsledku anharmonicity atom vibrací v krystalu. Fononové-fononové mechanismus tepelný odpor ((1/λ) je známý jako koeficient tepelného odporu) je možné pouze z důvodu přechodu následek zpomalení phonon toku a znatelné změně kvazi-hybnost. Čím vyšší je T, tím vyšší je pravděpodobnost přechodu s klesající:(1/T). Vzhledem k tomu, že při T > θD tepelná kapacita c se s teplotou jen mírně zvyšuje, λ1 / T.

Při teplotách nižších než Debye teplota, T<<θD, délka střední volná dráhaurčuje phonon-fononové rozptyl roste drasticky,expθD/T, a, jako pravidlo, je omezena na velikost krystalu R. Podle Debye zákona tepelná kapacita c je v tomto teplotním rozmezí se liší jak c(T/θD)3. V důsledku toho se při t → 0 musí koeficient tepelné vodivosti λ snížit v poměru k T3. Teplota, pro kterou má tepelná vodivost vrchol, se stanoví od≈ R, což běžně odpovídá t ≤ 0,05dd.

tato teorie také odpovídá za chování koeficientu tepelné vodivosti pro amorfní látky bez dlouhého dosahu, tj. velikost jejich „krystalů“ je řádově atomových velikostí. Z tohoto důvodu musí rozptyl na „hranicích“ těchto látek převládat vůbec T a≈ const. Koeficient tepelná vodivost amorfní látky λT3 při nízkých teplotách a musí mírně rostou, v poměru k tepelné kapacity, na střední a vysoké teploty, T > θD.

to Vše poskytuje kvalitativní vysvětlení závislost λ(T) v reálném krystalu dielektrika, ale nebere v úvahu odchylky od konstantní mříž v důsledku atomové nečistot z jiných prvků a jejich izotopy. Při vysoké teplotě je odpor, který je nabízen nečistotami k přenosu tepla, nezávislý na teplotě. To umožňuje odhadnout stupeň čistoty krystalů z kolísání jeho tepelné vodivosti s teplotou. Stejná skutečnost nám umožňuje určit rozložení mezi skelný a crystal látky v přírodní minerální případě, že sklo je považováno za nečistotu v krystalu.

tepelná vodivost v kovech závisí na pohybu a interakci proudových nosičů, tj. Obecně platí, že součinitel tepelné vodivosti λ kovu se rovná součtu mříž (phonon) λph a elektronů λe komponenty, λ = λe + λph; v běžných teplotách, jako pravidlo, λe >>λph.

Pokud budeme aplikovat jednoduché kinetická teorie plynů k toku volných elektronů a předpokládat, že délka jejich volná dráha nezávisí na rychlosti, pak teorie vyplývá, že

kde e je náboj elektronu, K Boltzrnann je konstantní, a σ je elektrická vodivost. Přísné kvantově mechanické teorie nabízí podobný vztahu,

V obou vzorců poměr elektronu část součinitel tepelné vodivosti λ na elektrickou vodivost σ, v širokém rozsahu teplot, se zdá být v poměru k teplotě podle Wiedemann-Franz zákon, λ/σ = LT, kde L je Lorentzova číslo. Tento zákon se používá k výpočtu λe z měřené elektrické vodivosti. Nicméně, to je porušena při teplotách pod θD, když elektron-fononové interakce převažuje (σ roste s klesající T jako T−5, zatímco le liší víc, něco jako T−2).

experimentální nálezy dokazují, že tepelná vodivost kovů při vysokých teplotách je zpravidla mírně klesající funkcí teploty. Existuje však mnoho výjimek. Tepelná vodivost železa tedy s teplotou silně klesá, zatímco tantal a niob vykazují kladný teplotní koeficient.

zajímavé jsou pokusy porovnat součinitele tepelné vodivosti pro různé látky pro jednu charakteristickou teplotu, například teplota tání Tm pevných látek. To znamená, že statistické zpracování experimentálních dat provádí Missenard ukázaly, že tepelná vodivost kovů na bod tání λ(T = Tm) = λm je v poměru k λa tepelná vodivost dielectrical krystaly v T = Tm je v poměru k, kde m je molekulová hmotnost, N počet atomů v chemickém vzorci, ρ hustota a teplota tání Tm je v Kelvinech.

Teplo dopravy v polovodičích je složitější než v dielektrika a kovy, protože phonon a elektronové komponenty jsou stejně důležité pro ně. Dalším důvodem složitosti je značný vliv nečistot, bipolární difúze a dalších málo studovaných faktorů na přenos tepla.

vliv tlaku na teplotní vodivost pevných látek lze předpokládat, s dobrou přesností, být lineární, λ, pro mnoho kovů roste s p.

na vliv pórovitosti na tepelnou vodivost pevných látek viz Porézní Médium.