Zjednodušení MKP Modely: rovinná napjatost a rovinná Deformace

Poznámka Editora: Tony Opatství učí žít NAFEMS FEA třídy v USA, Evropě a Asii. Vyučuje také e-learningové kurzy NAFEMS po celém světě. Kontakt .podrobnosti.

předchozí Desktop Engineering článku („Zjednodušit FEA Simulace Modelů Pomocí Rovinné Symetrie“) vysvětlil, že i s moderní výkonné počítače, tam je často motivace k využívání zjednodušení techniky, strukturální analýza metodou konečných prvků (FEA). Toto sledování popisuje, jak lze dvě úzce související metody použít k tomu, aby 2D řezy procházely složitou strukturou v oblastech zájmu. Výsledné modely FEA mohou poskytnout cenný vhled do místních napětí rychleji a efektivněji než úplný 3D model. Neřeknou celý příběh, ale jsou cennými nástroji pro inženýra CAE.

dvě metody FEA se nazývají rovinné napětí a rovinné napětí. Oba používají 2D rovinné prvky, které vypadají jako tenké skořepinové prvky a jsou spojeny pomocí rovinné geometrie povrchu.

Analýza Rovinného Napětí

Obr. 1 ukazuje důležitá fakta o rovinné stresové analýze. Předpokládá se, že konstrukční oblast leží v rovině 2D xy, přičemž třetí konstrukční rozměr je relativně malý. Na obrázku je to tloušťka ve směru z. Napětí existují ve 2D rovině jako sigma x, sigma y (přímé napětí) a sigma xy (smykové napětí v rovině). Každé z těchto napětí je konstantní tloušťkou, jak je znázorněno na vložce. Kromě toho nemůže být ve směru z žádný stres. Tento vztah napětí a deformace materiálu je definován ve 2D rovinných napěťových prvcích použitých v tomto typu analýzy.

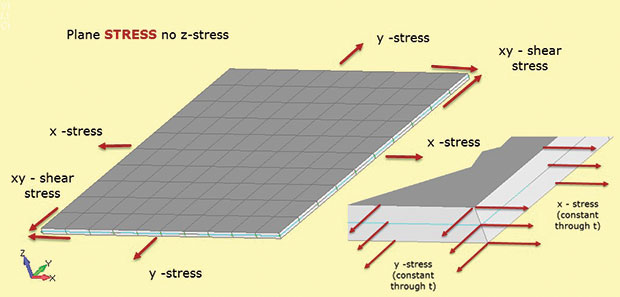obr. 1: rovinné napětí; předpoklady stresového stavu.

nedostatek napětí z je způsob, jak pamatovat na označení typu prvku rovinné napětí (tj. povoleno pouze napětí v rovině). Neexistují také žádné smykové napětí přes tloušťku. Mohli bychom načíst model rovinného napětí na obr. 1 s bi-axiální zatížení a výpočet sigma x a sigma y. Není sigma z. Můžeme také vypočítat odpovídající in-plane kmeny e-x a e-y. Pokud budeme aplikovat smykové zatížení, můžeme najít smykové napětí sigma xy a smykové namáhání e-xy. Zajímavé je, můžeme také vypočítat pomocí tloušťky kmene e-z. To není nula, protože model je zdarma tenký dolů v ose z, jak to táhne v x a y. Nemáme žádné out-of-plane constraint, aby se zabránilo to. V některých řešitelích můžeme obnovit průchozí kmen E-z a použít jej k výpočtu změny tloušťky. (Pokud je model v bi-axiální kompresi, sekce z bude silnější). To je obvykle považováno za sekundární kmen a nemusí být k dispozici pro výstup—ale je tam a lze jej v případě potřeby vypočítat ručně.

obr. 2 znázorňuje hliníkovou komponentu oka. Výstupek vyčnívá z kompozitního vrstvení, které má vrstvy umístěné a Spojené přes tangs (nebo nohy) a spodní část těla. Tangs přenášejí zatížení aplikované na výstupek do kompozitní struktury. V praxi by se vrstvy stupňovaly, aby se umožnil hladký smykový přenos vazbou do kompozitu. Smykové převod do kompozitního je simulované zde rozptýlené povrch trakční síly „tahání“ na stopky. Ty vyvažují použité zatížení oka.

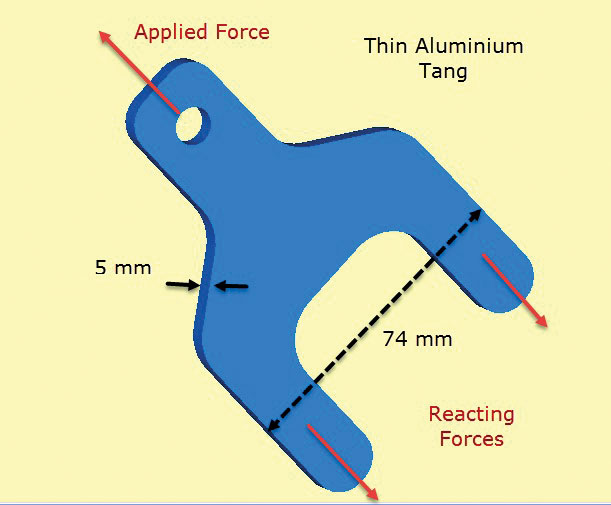obr. 2: Tenkostěnný hliník tang přenášení zatížení do kompozitní konstrukce.

klíčovým předpokladem je, že napětí v tloušťce jsou nulová a napětí v rovině jsou konstantní tloušťkou v komponentě. To znamená, že místní detail přenosu smykového zatížení z kompozitu do tangu je špatně modelován. Tato analýza se však zaměřuje na kontrolu dimenzování průřezu oka a tanga bez kompozitu, pomocí napětí v rovině.

tloušťka součásti je malá ve srovnání s jinými rozměry. Tato hodnota je zadána jako skutečná tloušťka v definici prvku rovinného napětí.

obr. 3 znázorňuje model FEA a vypočtené maximální hlavní napětí. Oblasti zájmu jsou kolem oka a poloměrů ramen. V reálném světě by stresový stav při koncentracích napětí byl 3D a prostřednictvím tloušťky sigma z napětí a smyková napětí by se vyrovnala lokálně. Zde je však velmi rozumné předpokládat, že dominují napětí v rovině. To je stejný předpoklad implicitní ve většině tradičních výpočtů koncentrace stresu (kt) nalezených v příručkách.

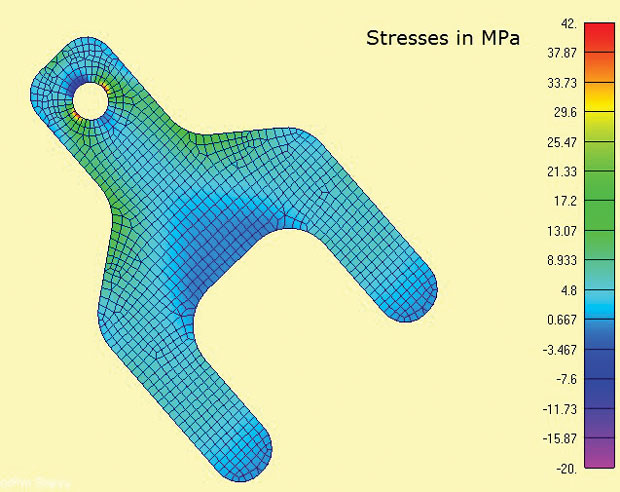Obr 3: 2D napětí v Rovině prvků, které ukazují maximální hlavní napětí

Jeden z výhodné vlastnosti napětí v rovině analýzy je, že je striktně 2D analýzu, takže jen tři stupně volnosti (DOF) musí být omezena (v-rovina překladů x, y a rotace kolem osy z). To se hodí k metodě minimálního omezení 3-2-1 s vyváženým zatížením. Ve 2D případě to degeneruje na metodu 2-1. Jeden uzel má DOF X a y omezené, druhý vhodný ortogonální uzel má DOF x omezený. To umožňuje, aby reakční zatížení v tangách bylo aplikováno přímo jako rozptýlené vyrovnávací zatížení. Bylo by obtížné simulovat tuto hraniční podmínku pomocí omezení na zemi.

průchozí tloušťka e-z kmene a tím i ztenčení tangs by se dalo vypočítat jako sekundární efekt.

Analýza Rovinných Kmenů

Obr. 4 ukazuje podstatu metody rovinného namáhání. Opět se používají 2D rovinné prvky, ale s jemně odlišnými předpoklady. Napětí v rovině x, y a xy jsou vyvíjeny jako dříve. Tentokrát je to však mimo rovinu, nebo přes tloušťku z kmen, který je nastaven na nulu. Takže analýza rovinných kmenů umožňuje pouze kmeny v rovině. To funguje dobře reprezentovat silné struktury, jako je znázorněno. Přítomnost tohoto velkého množství materiálu má tendenci stabilizovat komponentu a zabránit jejímu namáhání v z. To také znamená, že ve struktuře se vyvíjejí konstantní napětí v tloušťce z. Tento vztah materiálu napětí a deformace je definován ve 2D rovinných kmenových prvcích použitých v tomto typu analýzy.

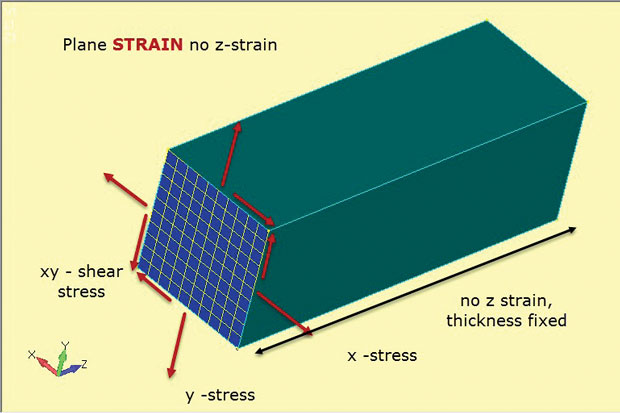obr. 4: Analýza rovinných deformací; předpoklady stavu napětí a deformace.

obrázek ukazuje orientaci 2D plane strain prvky jako řez řez typické hluboké součásti. Předpokládá se, že stresový stav v této řezné části bude duplikován při jakémkoli rovinném řezu xy (stanice z) přes komponentu. Předpokládá se, že komponenta je hranolová (má konstantní průřez) po celé délce.

v praxi používáme tuto metodu, kdy se stav napětí mění pomalu od roviny k rovině v hluboké složce. Měl by být dostatek materiálu přes hloubku stabilizovat a eliminovat průchozí napětí tloušťky. Jedná se o stejný princip používaný u vzorků lomové houževnatosti znázorněných na obr. 5. Selhání za podmínek rovinného namáhání je ukázáno pro středovou část tlustého vzorku. Porucha na volných okrajích a tenké části je jiný režim, spíše jako rovinný stresový stav. Letadlo kmen FEA model by podle definice být dobrou reprezentaci osy tlustý vzorek chování, ale ne volné hrany nebo tenké vzorky.

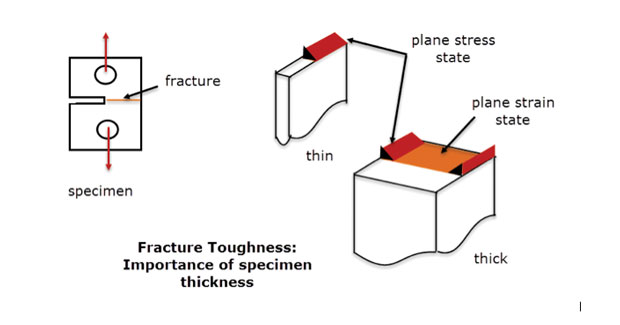obr. 5: vzorky lomové houževnatosti; tenké a silné sekce.

obr. 6 znázorňuje další složku použitou v kompozitní struktuře, tvořící pojený spoj. Zde je sekce konstantní a dostatečně hluboká, takže můžeme předpokládat, že napětí jsou také konstantní s hloubkou. Volný konec povrchu plochy (v +z, -z) bude mít jiný lokální napjatosti (plane stress, jak je uvedeno), nicméně cílem této analýzy je zjistit, sekce net zdůrazňuje na osu (z = 0).

2D rovinná síť pro analýzu kmenů je znázorněna na obr. 7. Řez řezu je definován na stanici z = 0.

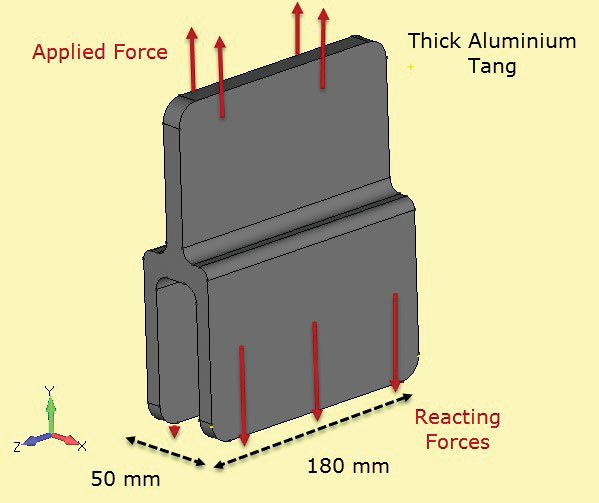Obr. 6: hliníkový plech s hlubokým průřezem.

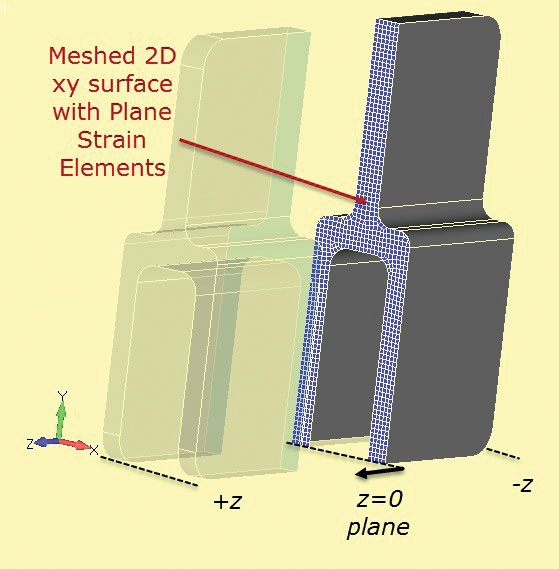obr. 7: Sekce proříznutá pevným průřezem pro vývoj 2D rovinného úseku.

lze použít velmi jemnou 2D rovinnou síťku, která poběží velmi rychle ve srovnání s plným 3D modelem. Metoda omezení 2-1 se používá jako dříve. Zatížení je třeba pečlivě zvážit. „Tloušťka“ sekce rovinného kmene je zcela libovolná a ve výchozím nastavení je obvykle nastavena na 1,0. Je-li zatížení komponenty vypočteno jako provozní zatížení hloubkou (N/m, Lbf/palec atd.) pak lze tuto hodnotu použít přímo na rovinném kmenovém pletivu. Je užitečné vybrat sekci, například jediný tang a odhadnout nominální nebo průměrné napětí v této sekci pro celou složku. To lze použít jako kontrolu zdravého rozumu v analýze rovinných kmenů. Nesprávné načítání je pravděpodobně hlavní příčinou chyby v této metodě.

výsledky analýzy jsou znázorněny na obr. 8 a jasně ukazují oblasti vysokého napětí kolem ramenního filé. Napětí platí pro oblast střední hloubky komponenty (z = 0).

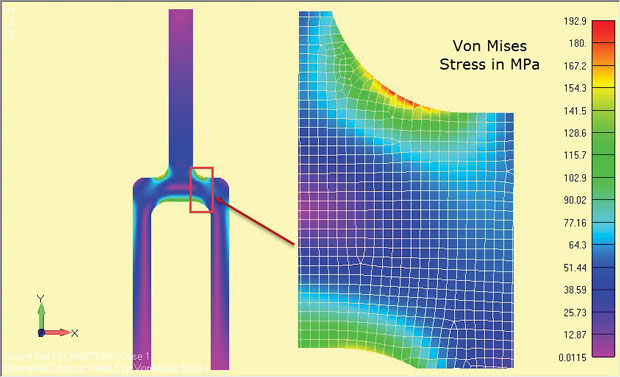obr. 8: Výsledky analýzy rovinných kmenů složky deep tang.

použité množství napětí bude záviset na použitém řešiči. Někteří řešitelé ignorují napětí ve směru z jako sekundární a obnovují napětí v rovině. Hlavní napětí a von Misesova napětí se pak vztahují k 2D stresovému stavu v rovině. Pokud je napětí ve směru z obnoveno, mělo by být jasně identifikováno, aby bylo možné identifikovat stav napětí 2D v rovině v rovině XY.

co přesně představuje stres směru z? Je to napětí vyvinuté v důsledku vynucování nulového směru z. Napětí působí, jako by byly volné koncové plochy hranolové části fixovány. Ve střední rovině složky hlubokého řezu to budou komplementární napětí potřebná k udržení stavu napětí ve směru nula z. Ve skutečnosti, jak jsme se přesunout směrem k volnému povrchu tváře, z-napětí klesne na nulu a stává se letadlo rozložení napětí (jak je vidět v husté lomové mechaniky vzorku).

v mnoha případech, jako je tlakový válec, jsou koncové plochy uzavřeny a ve skutečnosti vyvinou axiální napětí v důsledku axiálních sil. Bude to jiné napětí než indukované axiální napětí v analýze rovinných kmenů. Pro výpočet axiálních napětí bude nutný ruční výpočet, nebo možný doplňkový axisymetrický model pro tlakové nádoby.

snadnost geometrie a konstrukce pletiva se dobře hodí k“ what-if “ studiím nebo formálnějším studiím optimalizace tvarů.

pro srovnání byla provedena poloviční symetrická úplná 3D analýza komponenty deep tang a výsledky jsou znázorněny na obr. 9. Nominální napětí na horní jediné noze tang je v obou případech totožné-pamatujte, že toto je základ jakékoli kontroly zdravého rozumu.

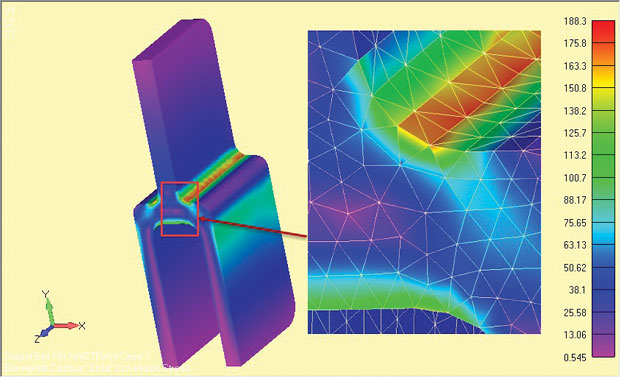obr. 9: plný 3D model hlubokého tangu, ukazující výsledky stresu.

lokální namáhání ramen je u celého modelu nižší o malé procento. To je ze tří důvodů. Za prvé, relativně hrubá 3D tet síť je nižší než velmi jemná 2D rovinná kmenová místní síť. Kontrola konvergence na 3D modelu nebyla provedena.

za Druhé, tam je malá změna v geometrii na volných plochách (+z, -z) ve srovnání s z = 0 bod kvůli konci filé. V tomto případě je účinek zanedbatelný, protože filé jsou mimo oblasti ramen. V mnoha komponentách však budou místní filety a dojdou detaily. který bude měnit geometrii od jednoduchého XY rovinné plochy. Lokální změny napětí na volných čelních plochách mohou být odhadnuty nebo zkontrolovány pomocí plného 3D modelu.

konečně, předpoklad rovinného kmene pevného omezení z Při + z, – z úsecích není pravdivý pro komponentu s konečnou hloubkou. Napětí z se rozptýlí na nulu na „skutečných“ volných tvářích. Tento efekt je znázorněn na obr. 10, který používá 3D model tak, jak je, a také jako simulaci rovinného napětí z napětí.

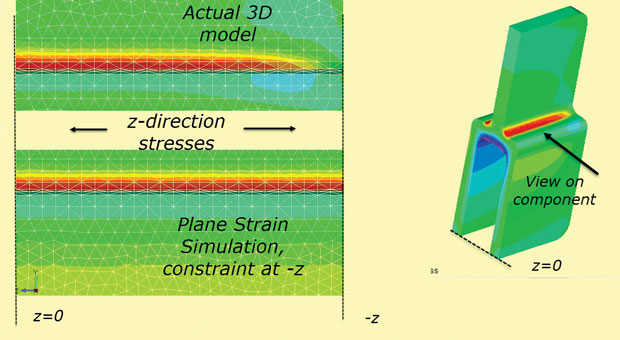obr. 10: difúze z-napětí směrem k volné ploše.

Rychlé a Efektivní

rovinné napjatosti a rovinné deformace analýzy jsou užitečné 2D metody, které lze často doplnit full-scale 3D modely. Ne všechny funkce mohou být zastoupeny, ale s určitou vynalézavostí lze alespoň odhadnout napětí v klíčových oblastech. Motivací pro použití těchto metod je umožnit rychlou efektivní analýzu se snadnou 2D geometrií a konstrukcí sítě.