Ahne algoritmi esimerkeillä: ahne menetelmä & lähestymistapa

ahneen lähestymistavan ymmärtämiseen tarvitaan toimiva tieto rekursiosta ja kontekstin vaihdosta. Tämä auttaa sinua ymmärtämään, miten jäljittää koodi. Ahneen paradigman voi määritellä omien välttämättömien ja riittävien lausuntojen perusteella.

ahneen paradigman määrittelee kaksi ehtoa.

• jokaisen Porrastetun ratkaisun on jäsenneltävä ongelma kohti parhaiten hyväksyttyä ratkaisuaan.
• riittää, jos ongelman jäsentäminen voi pysähtyä äärelliseen määrään ahneita askelia.

teoretisoinnin jatkuessa kuvatkaamme ahneen etsinnän lähestymistapaan liittyvää historiaa.

tässä ahne algoritmi opetusohjelma, opit:

• ahneiden algoritmien historia
• ahneet strategiat ja päätökset
• ahneen lähestymistavan ominaisuudet
• Miksi käyttää ahnetta lähestymistapaa?
• kuinka ratkaista toiminnan valintaongelma
• ahneuden Arkkitehtuuri
• ahneiden algoritmien haitat

ahneiden algoritmien historia

tässä on ahneiden algoritmien tärkeä maamerkki:

• ahneita algoritmeja konseptoitiin monille graafikävelyalgoritmeille 1950-luvulla.
• Esdger Djikstra konseptoi algoritmin tuottamaan mahdollisimman vähän spanning-puita. Hänen tavoitteenaan oli lyhentää Alankomaiden pääkaupungin Amsterdamin sisäisiä reittejä.
• samalla vuosikymmenellä Prim ja Kruskal saavuttivat optimointistrategiat, jotka perustuivat polkukustannusten minimointiin punnituilla reiteillä.
• 70-luvulla yhdysvaltalaiset tutkijat, Cormen, Rivest ja Stein ehdottivat ahneiden ratkaisujen rekursiivista alarakennetta klassisessa introduction to algorithms-kirjassaan.
• ahne hakuparadigma rekisteröitiin erilaisena optimointistrategiana NIST Recordsiin vuonna 2005.
• Till date, protokollat, jotka toimivat verkossa, kuten open-shortest-path-first (OSPF) ja monet muut verkon pakettikytkentäprotokollat käyttävät ahnetta strategiaa minimoidakseen verkossa vietetyn ajan.

ahneet strategiat ja päätökset

logiikka helpoimmassa muodossaan keitettiin muotoon ”ahne” tai ”ei ahne”. Nämä lausunnot määriteltiin lähestymistapa edetä kussakin algoritmin vaiheessa.

esimerkiksi Djikstran algoritmi hyödynsi portaittaista ahnetta strategiaa, joka tunnisti Internetin isännät laskemalla kustannusfunktion. Kustannusfunktion palauttama arvo määritteli, onko seuraava polku ”ahne”vai” ei-ahne”.

lyhyesti sanottuna algoritmi lakkaa olemasta ahne, jos se jossain vaiheessa ottaa askeleen, joka ei ole paikallisesti ahne. Ahneet ongelmat loppuvat ahneuden ulottumattomiin.

ahneen lähestymistavan ominaisuudet

ahneen menetelmän algoritmin tärkeät ominaisuudet ovat:

• on järjestetty luettelo resursseista, ja kustannukset tai arvonmääritys. Nämä määrälliset rajoitukset järjestelmään.
• otat käyttöön mahdollisimman suuren määrän resursseja rajoituksen voimassaoloaikana.
• esimerkiksi toiminnan aikatauluongelmassa resurssikustannukset ovat tunneissa, ja toiminnot on suoritettava sarjajärjestyksessä.

Miksi käyttää ahneutta?

tässä syitä käyttää ahnetta lähestymistapaa:

• ahneella lähestymistavalla on muutama tradeoffs, jotka saattavat tehdä siitä sopivan optimointiin.
• yksi merkittävä syy on saavuttaa mahdollisimman toteuttamiskelpoinen ratkaisu välittömästi. Jos toiminnan valintaongelmassa (selitetty alla) voidaan tehdä useampia toimintoja ennen nykyisen toiminnan lopettamista, nämä toiminnot voidaan suorittaa samassa ajassa.
• toinen syy on jakaa ongelma rekursiivisesti ehdon perusteella, eikä kaikkia ratkaisuja tarvitse yhdistää.
• aktiivisuusvalintaongelmassa ”rekursiivinen jako” – vaihe saavutetaan skannaamalla asialuettelo vain kerran ja tarkastelemalla tiettyjä toimintoja.

kuinka ratkaista toiminnan valintaongelma

toiminnan aikataulutusesimerkissä jokaiselle toiminnalle on” alku” ja ”lopetus” – aika. Jokainen toiminto on indeksoitu viitenumerolla. Toimintoluokkia on kaksi.

1. harkittu aktiivisuus: aktiivisuus, josta analysoidaan kykyä tehdä enemmän kuin yksi jäljellä oleva toiminta.
2. muut toiminnot: toiminnot yhdessä tai useammassa indeksissä ennen tarkasteltavaa toimintaa.

kokonaiskesto ilmoittaa toiminnan toteuttamiskustannukset. Se on (finish-start) antaa meille durational kuin kustannukset toimintaa.

saat tietää, että ahne laajuus on jäljellä olevien toimintojen määrä, jotka voit suorittaa harkitun toiminnan aikana.

ahneuden Arkkitehtuuri

Vaihe 1)

skannaa toimintakustannusten luettelo alkaen indeksistä 0.

Vaihe 2)

kun useampi toiminto on valmis siihen mennessä, kyseinen toiminto päättyy, aloita yhden tai useamman jäljellä olevan toiminnon etsiminen.

Vaihe 3)

jos jäljellä olevia toimintoja ei enää ole, nykyinen jäljellä oleva toiminta muuttuu seuraavaksi tarkasteltavaksi toiminnaksi. Toista vaihe 1 ja Vaihe 2 uudella harkitulla toiminnolla. Jos toimintoja ei ole jäljellä, siirry vaiheeseen 4.

Vaihe 4)

palauttakaa harkittujen indeksien liitto. Nämä ovat aktiivisuusindeksejä, joita käytetään maksimoimaan läpimeno.

koodin selitys

#include<iostream>#include<stdio.h>#include<stdlib.h>#define MAX_ACTIVITIES 12

koodin selitys:

1. sisältyi otsikkotiedostoja / luokkia
2. suurin määrä käyttäjän antamia toimintoja.

using namespace std;class TIME{ public: int hours; public: TIME() { hours = 0; }};

koodin selitys:

1. suoratoistotoimintojen nimiavaruus.
2. luokan määritelmä ajalle
3. tunnin aikaleima.
4. a AIKALAATIKON rakentaja
5. tuntimuuttuja.

class Activity{ public: int index; TIME start; TIME finish; public: Activity() { start = finish = TIME(); }};

koodin selitys:

1. luokan määritelmä toiminnosta
2. aikaleimat, jotka määrittelevät keston
3. kaikki aikaleimat alustetaan arvoon 0 oletuskonstruktorissa

class Scheduler{ public: int considered_index,init_index; Activity *current_activities = new Activity; Activity *scheduled;

koodin selitys:

1. ajoituksen luokan määritelmän Osa 1.
2. Considered Index on lähtötilanne joukon skannaamiselle.
3. alustusindeksiä käytetään satunnaisten aikaleimojen osoittamiseen.
4. aktiviteettiobjektien joukko jaetaan dynaamisesti uuden operaattorin avulla.
5. ajoitettu osoitin määrittelee ahneuden nykyisen pohjapaikan.

Scheduler(){ considered_index = 0; scheduled = NULL;......

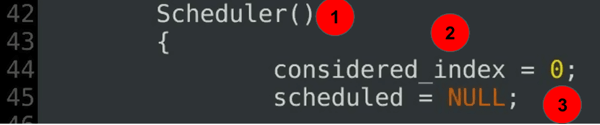
koodin selitys:

1. scheduler constructor – osa 2 scheduler class definition.
2. tarkasteltu indeksi määrittää nykyisen skannauksen alkamisajankohdan.
3. nykyinen ahne laajuus on alussa määrittelemätön.

for(init_index = 0; init_index < MAX_ACTIVITIES; init_index++) { current_activities.start.hours = rand() % 12; current_activities.finish.hours = current_activities.start.hours + (rand() % 2); printf("\nSTART:%d END %d\n", current_activities.start.hours ,current_activities.finish.hours); }……

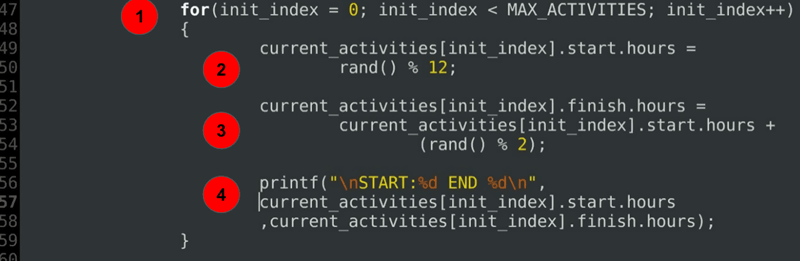
koodin selitys:

1. A silmukka, jolla käynnistetään kunkin suunnitellun toiminnan alkamis-ja päättymisajat.
2. aloitusaika alustus.
3. päättymisaika alustetaan aina alkutunnin jälkeen tai tarkalleen.
4. vianetsintälauseke jaettujen kestojen tulostamiseksi.

public: Activity * activity_select(int);};

koodin selitys:

1. osa 4-The last part of the scheduler class definition.
2. Activity select-funktio ottaa lähtökohdan indeksin pohjaksi ja jakaa ahneen etsinnän ahneisiin osaongelmiin.

Activity * Scheduler :: activity_select(int considered_index){ this->considered_index = considered_index; int greedy_extent = this->considered_index + 1;…… 

1. funktion määritelmä annetaan scope resolution operator (::) – toiminnon avulla.
2. tarkasteltu indeksi on indeksi, jota kutsutaan arvon mukaan. Greedy_extent on alustettu vain indeksi jälkeen tarkastellaan indeksi.

Activity * Scheduler :: activity_select(int considered_index){ while( (greedy_extent < MAX_ACTIVITIES ) && ((this->current_activities).start.hours < (this->current_activities).finish.hours )) { printf("\nSchedule start:%d \nfinish%d\n activity:%d\n", (this->current_activities).start.hours, (this->current_activities).finish.hours, greedy_extent + 1); greedy_extent++; }…...

koodin selitys:

1. peruslogiikka-ahne laajuus rajoittuu toiminnan määrään.
2. nykyisen toiminnon alkutunnit tarkistetaan ajoituksen mukaisiksi ennen kuin kyseinen toiminto (annettu tarkasteltuna indeksinä) päättyisi.
3. niin kauan kuin mahdollista, tulostetaan valinnainen vianetsintälauseke.
4. Advance to next index on the activity array

...if ( greedy_extent <= MAX_ACTIVITIES ) { return activity_select(greedy_extent); } else { return NULL; }}

koodin selitys:

1. ehdolliset tarkastukset, jos kaikki toiminnot on katettu.
2. jos ei, voit aloittaa ahnehtimisen uudelleen tarkasteltavan indeksin ollessa nykyinen piste. Tämä on rekursiivinen vaihe, joka ahnaasti jakaa ongelmalausunnon.
3. jos kyllä, se palaa soittajalle ilman sijaa ahneuden laajentamiselle.

int main(){ Scheduler *activity_sched = new Scheduler(); activity_sched->scheduled = activity_sched->activity_select( activity_sched->considered_index); return 0;}

koodin selitys:

1. päätoiminto, jota käytetään ajastimen kutsumiseen.
2. uusi aikataulu on instantioitu.
3. activity select-funktio, joka palauttaa aktiviteettityyppisen osoittimen, palaa soittajalle, kun ahne etsintä on ohi.

Lähtö:

START:7 END 7START:9 END 10START:5 END 6START:10 END 10START:9 END 10Schedule start:5 finish6 activity:3Schedule start:9 finish10 activity:5

ahneiden algoritmien haitat

se ei sovellu ahneisiin ongelmiin, joissa jokaiseen osaongelmaan kuten lajitteluun tarvitaan ratkaisu.

tällaisissa ahneissa algoritmikäytännön ongelmissa ahne menetelmä voi olla väärä; pahimmassa tapauksessa johtaa jopa epäoptimaaliseen ratkaisuun.

ahneiden algoritmien haittapuolena on siis se, ettei tiedetä, mikä on nykyisen ahneen tilan edessä.

alla on kuvaus ahneen menetelmän haitasta:

vuonna ahne skannaus näkyy tässä puu (suurempi arvo suurempi ahneus), algoritmi tila arvo: 40, todennäköisesti ottaa 29 kuin seuraava arvo. Lisäksi sen etsintä päättyy 12. Tämä on arvo 41.

kuitenkin, jos algoritmi valitsi epäoptimaalisen polun tai omaksui valloittavan strategian. sen jälkeen 25: tä seuraisi 40, ja yleinen kustannusparannus olisi 65, mikä on 24 prosenttiyksikköä korkeampi osaoptimaalisena päätöksenä.

esimerkkejä ahneista algoritmeista

useimmat verkkoalgoritmit käyttävät ahneutta. Tässä on luettelo harvoista ahne algoritmi esimerkkejä:

• Primin Minimaalipuualgoritmi
• Kauppamatkustajan ongelma
• Graph – kartan väritys
• Kruskalin Minimaalipuualgoritmi
• Dijkstran Minimaalipuualgoritmi
• Graph – Vertex Cover
• knapsack-ongelma
• työn Aikatauluongelma

Yhteenveto:

Yhteenvetona artikkelissa määriteltiin ahne paradigma, osoitettiin kuinka ahne optimointi ja rekursio voivat auttaa saamaan parhaan ratkaisun tiettyyn pisteeseen asti. Ahne algoritmi on laajalti otettu sovellus ongelmanratkaisuun monissa kielissä ahne algoritmi Python, C, C#, PHP, Java, jne. Activity valinta ahne algoritmi esimerkki kuvattiin strateginen ongelma, joka voisi saavuttaa suurimman läpimenon käyttämällä ahne lähestymistapa. Lopulta selitettiin ahneen lähestymistavan käytön heikennykset.