SSIM esiteltiin ensimmäisen kerran vuonna 2004 IEEE: n julkaisussa Image Quality Assessment: from Error Visibility to Structural Similarity. Abstrakti tarjoaa hyvän intuition ajatukseen ehdotetun järjestelmän takana,
objektiivisilla kuvanlaadun arviointimenetelmillä on perinteisesti pyritty kvantifioimaan vääristyneen kuvan ja viitekuvan välisten virheiden (eroavaisuuksien) näkyvyyttä käyttämällä erilaisia ihmisen näköjärjestelmän tunnettuja ominaisuuksia. Olettaen, että ihmisen näköhavainto soveltuu hyvin rakenteellisen tiedon erottamiseen kohtauksesta, otamme käyttöön vaihtoehtoisen täydentävän kehyksen rakenteellisen tiedon heikkenemiseen perustuvalle laadunarvioinnille.
Yhteenveto: kirjoittajat esittävät 2 olennaista kohtaa,
- useimmat kuvanlaadun arviointitekniikat perustuvat vertailu-ja näytekuvan välisten virheiden kvantifiointiin. Yhteinen metriikka on määrittää kunkin vastaavan pikselin arvojen ero otoksen ja viitekuvan välillä (käyttämällä esimerkiksi Keskivertovirhettä).
- ihmisen näköhavaintojärjestelmä pystyy erittäin hyvin tunnistamaan Rakennetiedot kohtauksesta ja siten tunnistamaan erot vertailu-ja näytetiedon välillä. Näin ollen metriikka, joka jäljittelee tätä käyttäytymistä, toimii paremmin tehtävissä, joihin liittyy näytteen ja referenssikuvan erottaminen toisistaan.
Structural Similarity Index (SSIM) – metriikka poimii kuvasta 3 keskeistä piirrettä:
- Luminanssi
- Kontrasti
- rakenne
kahden kuvan vertailu suoritetaan näiden 3 piirteen perusteella.
alla olevassa kuvassa 1 esitetään rakenteellisen samankaltaisuuden mittausjärjestelmän järjestely ja virtaus. Signaali X ja signaali Y viittaavat viite-ja Näytekuviin.

mutta mitä tämä metriikka laskee?
tämä järjestelmä laskee rakenteellisen Samankaltaisuusindeksin 2 annetun kuvan välille, joka on arvo välillä -1 ja +1. Arvo +1 osoittaa, että 2 annetut kuvat ovat hyvin samanlaisia tai samoja, kun taas arvo -1 osoittaa, että 2 annetut kuvat ovat hyvin erilaisia. Usein nämä arvot säädetään niin , että ne ovat alueella, jossa ääripäillä on sama merkitys.
nyt tutkitaan lyhyesti, miten nämä piirteet esitetään matemaattisesti ja miten ne vaikuttavat lopulliseen SSIM-pistemäärään.
- Luminanssi: Luminanssi mitataan keskiarvona kaikista pikseliarvoista. Sen merkitään μ (Mu) ja kaava on esitetty alla,
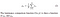
- Kontrasti: Se mitataan ottamalla keskihajonta (varianssin neliöjuuri) kaikista pikselin arvoista. Sitä merkitään σ: lla (sigma) ja esitetään alla olevalla kaavalla,
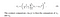
- Rakenne: Rakenteellinen vertailu tehdään käyttämällä konsolidoitua kaavaa (enemmän siitä myöhemmin), mutta pohjimmiltaan jaamme tulosignaalin sen keskihajonta niin, että tulos on yksikkö keskihajonta, joka mahdollistaa vankemman vertailun.
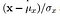
joten nyt olemme vakiinnuttaneet matemaattisen intuition kolmen parametrin taakse. Mutta pidä kiinni! Laskutoimitus on vielä kesken, vähän enemmän. Mitä meiltä puuttuu nyt, ovat vertailutoiminnot, jotka voivat vertailla kahta annettua kuvaa näillä parametreilla, ja lopuksi, yhdistelmäfunktio, joka yhdistää ne kaikki. Tässä määritellään vertailufunktiot ja lopuksi yhdistelmäfunktio, jolla saadaan samankaltaisuusindeksin arvo
- Luminanssivertailufunktio: se määritellään funktiolla l(x, y), joka on esitetty alla. μ (mu) tarkoittaa annetun kuvan keskiarvoa. x ja y ovat kaksi kuvaa verrataan.
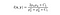
missä C1 on vakio vakauden varmistamiseksi, kun nimittäjästä tulee 0. C1 saadaan,
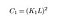
päivitys: koko artikkeli, emme olleet tutkineet, mitä K ja L vakiot tässä yhtälössä ovat. Onneksi lukija huomautti, että kommentit, ja niin edun tehdä tämän artikkelin hieman avulias, minä vain määritellä ne täällä.
l on pikseliarvojen dynaaminen alue (asetamme sen arvoksi 255, koska kyseessä ovat tavalliset 8-bittiset kuvat). Voit lukea lisää siitä, mitkä ovat eri kuvatyypit ja mitä ne tarkoittavat, täältä.
K1, K2 ovat ihan normaalivakioita, ei siinä paljon mitään!
- Kontrastivertailufunktio: se määritellään seuraavassa esitetyllä funktiolla c (x, y). σ tarkoittaa tietyn kuvan keskihajontaa. x ja y ovat kaksi kuvaa verrataan.
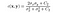
jossa C2 on annettu,
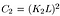
- rakenteen vertailufunktio: se määritellään funktiolla s (x, y), joka on esitetty alla. σ tarkoittaa tietyn kuvan keskihajontaa. x ja y ovat kaksi kuvaa verrataan.
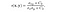
jossa σ(xy) määritellään seuraavasti:,
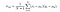
ja lopuksi, SSIM pisteet annetaan,

missä α > 0, β > 0, γ > 0 tarkoittavat kunkin mittarin suhteellista merkitystä. Yksinkertaistaaksemme lauseketta, jos oletamme, α = β = γ = 1 ja C3 = C2 / 2, voimme saada,
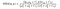
mutta siinä on juonenkäänne!
vaikka SSIM olisi mahdollista toteuttaa yllä mainituilla kaavoilla, mahdollisuudet ovat, että se ei ole yhtä hyvä kuin käytettävissä olevat käyttövalmiit toteutukset, kuten kirjoittajat selittävät, että,
kuvanlaadun arvioinnissa on hyvä soveltaa SSIM-indeksiä paikallisesti eikä maailmanlaajuisesti. Ensinnäkin kuvan tilastolliset ominaisuudet ovat yleensä hyvin spatiaalisesti ei-tilastollisia. Toiseksi, kuvavääristymät, jotka voivat riippua paikallisista kuvatilastoista tai eivät, voivat olla myös avaruusmuunnoksia. Kolmanneksi tyypillisillä katseluetäisyyksillä ihmisen havaitsija voi yhdellä kerralla havaita vain kuvan lähialueen suurella resoluutiolla (HVS: n foveaatio-ominaisuuden vuoksi , ). Ja lopuksi, lokalisoitu laadun mittaus voi tarjota tilakohtaisesti vaihtelevan laatukartan kuvasta, joka antaa enemmän tietoa kuvan laadun heikkenemisestä ja voi olla hyödyllinen joissakin sovelluksissa.
Yhteenveto: Sen sijaan, että edellä mainittuja mittareita sovellettaisiin globaalisti (eli koko kuvalle kerralla), on parempi soveltaa mittareita alueellisesti (eli pienissä osissa kuvaa ja ottamalla keskiarvo).
tätä menetelmää kutsutaan usein keskimääräiseksi rakenteelliseksi Samankaltaisuusindeksiksi.
tämän lähestymistavan muutoksen vuoksi myös kaavojamme on syytä muuttaa vastaamaan samaa (on huomattava, että tämä lähestymistapa on yleisempi ja sitä käytetään koodin selittämiseen).
(Huom: jos alla oleva sisältö tuntuu hieman ylivoimaiselta, ei hätää! Jos saat ydin siitä, sitten läpi koodi antaa sinulle paljon selkeämpi ajatus.)
kirjoittajat käyttävät 11×11-ympyräsymmetristä Gaussin Punnitusfunktiota (periaatteessa 11×11-matriisia, jonka arvot on johdettu Gaussin jakaumasta), joka liikkuu pikseli kerrallaan koko kuvan päällä. Kussakin vaiheessa paikallisen ikkunan sisällä lasketaan paikalliset tilastot ja SSIM-indeksi. Koska laskemme nyt mittareita paikallisesti, kaavojamme tarkistetaan,
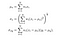
missä wi on Gaussin painotusfunktio.
jos tämä oli mielestäsi vähän tahaton, ei hätää! Riittää, kun kuvittelee Wiin multiplicandiksi, jota käytetään tarvittavien arvojen laskemiseen joidenkin matemaattisten temppujen avulla.
kun laskelmat on tehty koko kuvalle, otetaan vain kaikkien paikallisten SSIM-arvojen keskiarvo ja päädytään globaaliin SSIM-arvoon.
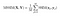
lopultakin teoria on valmis! Nyt koodiin!