olen aloittanut Andrew Ng: n suositun koneoppimiskurssin tekemisen Courseralla. Ensimmäinen viikko kattaa paljon, ainakin sellaiselle, joka ei ole muutamaan vuoteen juurikaan koskenut laskutoimituksiin
- Kustannusfunktiot (keskimääräinen ero neliöön)
- Gradient Descent
- lineaarinen regressio
nämä kolme aihetta olivat paljon sulateltavaa. Puhun jokaisesta yksityiskohtaisesti, ja miten ne kaikki sopivat yhteen, jonkun python-koodin osoittamiseksi.
Edit 4. toukokuuta: Julkaisin seurannan, jossa keskityin siihen, miten Kustannusfunktio toimii täällä, mukaan lukien intuitio, miten se lasketaan käsin ja kaksi erilaista Python-toteutusta. Voin tehdä liukuvärilaskun ja koota ne pian lineaariseen regressioon.
Malliesitys
ensinnäkin useimpien koneoppimisalgoritmien tavoitteena on rakentaa malli: hypoteesi, jota voidaan käyttää Y: n arvioimiseen X: n perusteella.hypoteesi eli malli kartoittaa sisääntuloja tuotoksiin. Eli esimerkiksi, jos koulutan mallin, joka perustuu kasaan asuntotietoja, jotka sisältävät talon koon ja myyntihinnan. Kouluttamalla mallin voin antaa sinulle arvion siitä, kuinka paljon voit myydä talosi sen koon perusteella. Tämä on esimerkki regressio-ongelmasta-kun otetaan huomioon jokin panos, haluamme ennustaa jatkuvan tuotoksen.
hypoteesi esitetään yleensä näin

theeta-arvot ovat muuttujia.
joitakin nopeita esimerkkejä siitä, miten visualisoimme hypoteesin:
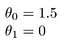
tällöin saadaan h(x) = 1,5 + 0x. 0x tarkoittaa ei kaltevuus, ja y on aina vakio 1.5. Tämä näyttää:

miten
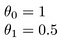

mallin luomisen tavoitteena on valita parametrit eli theta-arvot siten, että H (x) on lähellä Y: tä harjoitustiedoille, x: lle ja y: lle. Joten nämä tiedot
x =
y =

yritän löytää parhaiten sopivan linjan lineaarisen regression avulla. Aloitetaan.
Kustannusfunktio
tarvitsemme funktion, joka minimoi parametrit aineistomme yllä. Yksi yleinen funktio, jota käytetään usein, on keskimääräinen neliövirhe, joka mittaa estimaattorin (aineisto) ja estimoidun arvon (ennuste) välistä eroa. Se näyttää tältä.:

käy ilmi, että yhtälöä voi hieman säätää, jotta laskutoimitus raitaa pitkin olisi hieman yksinkertaisempaa. Päädymme:
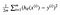
sovelletaan tätä konst-funktiota seuraaviin tietoihin:

nyt laskemme joitakin theta-arvoja ja piirrämme kustannusfunktion käsin. Koska tämä funktio kulkee (0, 0), tarkastelemme vain yhtä thetan arvoa. Tästä eteenpäin viittaan kustannusfunktioon nimellä J (Θ).
J: lle (1) saadaan 0. Ei yllätys-arvo J (1) tuottaa suora viiva, joka sopii tiedot täydellisesti. Entä J (0,5)?

MSE-funktio antaa arvoksi 0,58. Piirtäkäämme molemmat arvomme tähän mennessä:
J(1) = 0
J (0, 5) = 0.58

menen eteenpäin ja laskea joitakin arvoja J (Θ).

ja jos liitämme pisteet yhteen nätisti…

voimme nähdä, että kustannusfunktio on minimissään, kun theta = 1. Tämä on järkevää-meidän alustavat tiedot on suora viiva, jonka kaltevuus on 1 (oranssi viiva yllä olevassa kuvassa).
Gradient Descent
minimoimme J: n(Θ) yrityksen ja erehdyksen avulla — kokeilimme vain paljon arvoja ja tarkastimme tuloksena olevan kuvaajan silmämääräisesti. Täytyy olla parempi keino? Jonon gradientin laskeutuminen. Gradient Descent on yleinen funktio jonkin funktion minimoimiseksi, tässä tapauksessa Keskivertovirhekustannusfunktio.
Gradient Descent periaatteessa vain tekee sen, mitä teimme käsin — muuttaa theta-arvoja eli parametreja, vähän kerrallaan, kunnes saavuimme toivottavasti minimiin.
aloitetaan alustamalla theta0 ja theta1 mille tahansa kahdelle arvolle, sanotaan 0 kummallekin, ja jatketaan siitä. Muodollisesti algoritmi on seuraava:

missä α, alfa, on oppimistahti eli kuinka nopeasti haluamme edetä kohti minimiä. Jos α on kuitenkin liian suuri,voimme ylittää sen.

kaiken yhdistäminen-lineaarinen regressio
nopeasti tiivistettynä:
meillä on hypoteesi:

, jonka pitää sopia harjoitustietoihimme. Voimme käyttää kustannusfunktio kuten keskimääräinen potenssiin virhe:

jonka voimme minimoida gradientin laskeutumisen avulla:

, joka johtaa meidät ensimmäiseen koneoppimisen algoritmiin, lineaariseen regressioon. Viimeinen pala palapeliä, joka meidän on ratkaistava saadaksemme toimivan lineaarisen regressiomallin, on kustannusfunktion osittainen derivaatta:
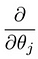
, joka osoittautuu:
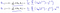
mikä antaa meille lineaarisen regression!
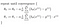
kun teoria on poissa tieltä, siirryn toteuttamaan tämän logiikan Pythonissa seuraavassa kirjoituksessa.
Edit 4.toukokuuta: julkaisin seurannan, jossa keskityin siihen, miten Kustannusfunktio toimii tässä, sisältäen intuition, miten se lasketaan käsin ja kaksi erilaista Python-toteutusta. Voin tehdä liukuvärilaskun ja koota ne pian lineaariseen regressioon.