Lämmönjohtavuus

kiinteiden aineiden lämmönjohtavuus on erilainen riippuen siitä, ovatko ne johtimia vai eivät. Dielektriikassa, jossa ei ole vapaita sähkövarauksia, lämpöenergiaa siirretään fononeilla. Kidehilan atomien kollektiiviset värähtelyt ilmenevät Siirtymä-aaltoina, joiden interferenssistä syntyy aaltopaketteja eli fononeja. Siirtymä-aallot aiheuttavat tiheyden vaihteluita, jotka voivat ilmetä taitekertoimen vaihteluna. Jos aallot kulkevat alueen läpi, jossa taitekerroin poikkeaa keskimääräisestä tilavuusarvosta, myöhemmät lämpöliikkeen energiaa kantavat siirtoaallot hajaantuvat.

sironta on sitä voimakkaampaa, mitä suurempi on atomien suurin poikkeama niiden keskipaikoista hilassa eli sitä suurempi T. Tämä selittää kokeellisesti todetun tosiasian, että kidesäteilyn lämmönjohtavuus vähenee melko korkeissa lämpötiloissa: λ1 / T (kuva 1).

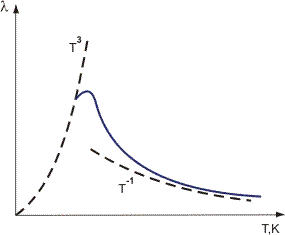
Kuva 1. Vaihtelu lämmönjohtavuus crystal dielectrics lämpötilan.

Debye esitti kvanttimekaanisten käsitteiden puitteissa oivalluksen λ(T) – variaation piikkimäisestä luonteesta matalalla T: llä. Hän laati dielektriikan dipoliteorian, joka perustuu molekyylin käsitteeseen jäykkänä dipolina. Tässä mallissa Debye esitteli käsitteen niin sanottu Debyen lämpötila θD verrannollinen atomien värähtelyjen maksimitaajuuteen kiinteässä. Useimmille aineille θD on joko huonelämpötilaa alhaisempi tai lähellä sitä (poikkeuksena on timantti, jolle θD = 1850 K ja berrylium, jolle θD = 1160 K).

kiinteiden aineiden kvanttiteoriassa kidehila katsotaan fononikaasulla täytetyksi tilavuudeksi, johon sovelletaan yksinkertaisimman kineettisen teorian deduktiota

missä c on dielektrisen lämpökapasiteetti, joka vastaa fononikaasun lämpökapasiteettia, v fononien keskimääräinen nopeus suunnilleen yhtä suuri kuin äänen nopeus,fononien keskimääräinen vapaa polku. Tietyn äärellisen arvonolemassaolo on seurausta fononien sironnasta fononeihin, kidehilan virheisiin ja erityisesti raerajoihin koko kappaleen yli. Lämpötilariippuvuus λ (T)määräytyy siten, ettäja C lämpötilasta.

korkeissa lämpötiloissa, jotka ylittävät huomattavasti Debyen lämpötilan θD, perusmekanismi, joka rajoittaa, on fononin ja fononin sironta, joka johtuu atomin värähtelyjen anharmonisuudesta kiteessä. Phononin ja fononin välinen lämpövastusmekanismi ((1/λ) tunnetaan lämpövastuskertoimena) on toteutettavissa vain siirtymän vuoksi, joka johtaa fononin virtauksen hidastumiseen ja kvasimomentin huomattavaan muuttumiseen. Mitä suurempi T, sitä suurempi todennäköisyys siirtymällepienenee:(1/T). Koska T > θD lämpökapasiteetti c kasvaa vain hieman lämpötilan myötä, näin ollen λ1 / T.

Debyen lämpötilaa alhaisemmissa lämpötiloissa, T<<θD, fononin ja fononin sironnan määrittämän vapaan keskitien pituuskasvaa rajusti,expθD/T ja rajoittuu pääsääntöisesti kide R: n kokoon.Debyen lain mukaan lämpökapasiteetti c tällä lämpötila-alueella vaihtelee C(T/θD)3. Näin ollen lämpötilassa t → 0 lämmönjohtavuuskertoimen λ täytyy pienentyä suhteessa T3: een. Lämpötila, jolle lämmönjohtavuuden huippu on määritetty≈ R, mikä vastaa yleisesti t ≤ 0,05 θD.

tämä teoria selittää myös niiden amorfisten aineiden lämmönjohtavuuskertoimen käyttäytymisen, joilla ei ole pitkän kantaman järjestystä, eli niiden ”kiteiden” koko on atomikokojen luokkaa. Tämän vuoksi sironnan näiden aineiden ”rajoilla” on vallittava kaikilla T ja≈ const. Amorfisten aineiden lämmönjohtavuuskerroin λT3 alhaisissa lämpötiloissa ja sen on kasvettava hieman suhteessa lämpökapasiteettiin kohtalaisissa ja korkeissa lämpötiloissa, T > θD.

kaikki tämä antaa kvalitatiivisen selityksen riippuvuudelle λ(T) todellisissa kideradikaaleissa, mutta ei ota huomioon poikkeamia vakiohilasta, joka johtuu muiden alkuaineiden ja niiden omien isotooppien atomiepäpuhtauksista. Korkeassa lämpötilassa epäpuhtauksien lämmönkuljetukselle tarjoama vastus on lämpötilasta riippumaton. Näin voidaan arvioida Kiteen puhtausaste sen lämmönjohtavuuden vaihtelusta lämpötilan kanssa. Saman tosiasian avulla voidaan määrittää lasimaisen ja kidemäisen aineen jakautuminen luonnollisessa mineraalissa, jos lasia pidetään Kiteen epäpuhtautena.

metallien lämmönjohtavuus riippuu virrankantajien eli johtoelektronien liikkeestä ja vuorovaikutuksesta. Yleensä metallin lämmönjohtavuuskerroin λ on yhtä suuri kuin hilan (fononin) λph ja elektronin λe komponenttien summa λ = λe + λph; tavallisissa lämpötiloissa pääsääntöisesti λe >>λph.

jos sovellamme kaasujen yksinkertaista kineettistä teoriaa vapaiden elektronien virtaukseen ja oletamme, että niiden vapaan reitin pituus ei riipu nopeudesta, niin teoria antaa ymmärtää, että

missä e on elektronin varaus, K Boltzrnannin vakio ja σ sähkönjohtavuus. Tiukka kvanttimekaaninen teoria tarjoaa samanlaisen suhteen,

molemmissa kaavoissa lämmönjohtavuuskertoimen λ elektroniosan suhde sähkönjohtavuuteen σ näyttää laajalla lämpötila-alueella olevan suhteessa Wiedemannin-Franzin lain mukaiseen lämpötilaan λ/σ = LT, missä L on Lorentzin luku. Tätä lakia käytetään λe: n laskemiseen mitatusta Sähkönjohtavuudesta. Sitä kuitenkin rikotaan alle θD: n lämpötiloissa, kun elektronin ja fononin vuorovaikutus vallitsee (σ kasvaa vähenevällä T: llä T-5: ksi, kun taas le vaihtelee hieman T−2: ksi).

kokeelliset löydökset osoittavat, että yleensä metallien lämmönjohtavuus korkeissa lämpötiloissa on hieman laskeva lämpötilan funktio. Poikkeuksia on kuitenkin monia. Siten raudan lämmönjohtavuus laskee voimakkaasti lämpötilan myötä, kun taas tantaali ja niobium osoittavat positiivisen lämpötilakertoimen.

kiinnostavia ovat yritykset vertailla eri aineiden lämmönjohtavuuden kertoimia yhdelle ominaislämpötilalle, esimerkiksi kiinteiden aineiden sulamispisteelle Tm. Niinpä Missenardin suorittama kokeellisten tietojen tilastollinen käsittely on osoittanut, että metallien lämmönjohtavuus sulamispisteessä λ(T = Tm) = λm on suhteessa arvoon λja dielektristen kiteiden lämmönjohtavuus pisteeseen t = Tm on suhteessa arvoon, missä m on molekyylimassa, N atomien lukumäärä kemiallisessa kaavassa, ρ tiheys ja sulamispiste Tm on kelvineissä.

lämmönsiirto puolijohteissa on monimutkaisempaa kuin dielektrisissä ja metalleissa, koska fononi ja elektronikomponentit ovat niille yhtä välttämättömiä. Toinen syy monimutkaisuuteen on epäpuhtauksien, bipolaarisen diffuusion ja muiden vähän tutkittujen tekijöiden huomattava vaikutus lämmönsiirtoon.

paineen vaikutuksen kiinteiden aineiden lämmönjohtavuuteen voidaan hyvällä tarkkuudella olettaa olevan lineaarinen, λ monille metalleille, jotka kasvavat p.

huokoisuuden vaikutuksesta kiinteiden aineiden lämmönjohtavuuteen katso huokoinen väliaine.