sähkökenttä E voidaan aina ilmaista skalaaripotentiaalifunktion gradienttina
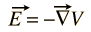
magneettikentälle B ei ole yleistä skalaaripotentiaalia, mutta se voidaan ilmaista vektorifunktion kaarena
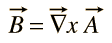
funktiolle A on annettu nimi ”vektoripotentiaali”, mutta se ei suoraan liity työhön samalla tavalla kuin skalaaripotentiaali on.
vektoripotentiaali määritellään ampeerin lain mukaiseksi ja se voidaan ilmaista joko virran I tai virran tiheyden j (magneettikentän lähteet) avulla. Eri teksteissä tämä määritelmä saa muotoja
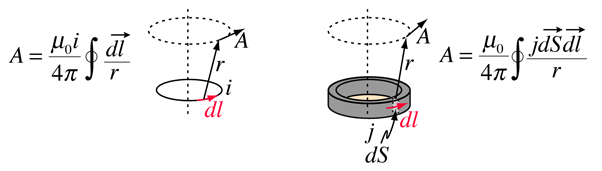
yksi peruste vektoripotentiaalille on, että vektoripotentiaalin laskeminen voi olla helpompaa kuin magneettikentän laskeminen suoraan tietystä lähdevirran geometriasta. Sen yleisin sovellus on antenniteoria ja sähkömagneettisten aaltojen kuvaus.
koska magneettikenttä B on määritelty A: n kaarevuudeksi ja vektorin identiteetin mukaan gradientin kaarevuudeksi on identtisesti nolla, voidaan A: han lisätä mikä tahansa mielivaltainen funktio, joka voidaan ilmaista skalaarifunktion gradienttina muuttamatta siitä saatavaa B: n arvoa. Toisin sanoen A ’ voidaan vapaasti korvata A: lla, jossa
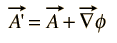
tällaisia muunnoksia kutsutaan mittamuunnoksiksi, ja on ollut useita ”mittareita”, joita on käytetty hyödyttämään on tietyntyyppisiä laskelmia sähkömagneettisessa teoriassa.