Opi OpenCV

tässä viestissä, opimme yksityiskohtia Histogrammi suuntautunut gradientit (HOG) ominaisuuskuvauksen. Saamme tietää, mitä konepellin alla on ja miten tämä asiasana lasketaan sisäisesti OpenCV: n, MATLABin ja muiden pakettien avulla.

tämä postaus on osa sarjaa, jota kirjoitan Kuvantunnistuksesta ja objektien tunnistamisesta.

alla on täydellinen luettelo tämän sarjan tutoraaleista:

1. kuvantunnistus perinteisillä Tietokonenäkötekniikoilla : Osa 1
2. suunnattujen kaltevuuksien Histogrammi : Osa 2
3. kuvantunnistuksen esimerkkikoodi : Osa 3
4. paremman näköilmaisimen koulutus: osa 4a
5. objektin havaitseminen perinteisillä Tietokonenäkötekniikoilla : osa 4b
6. Oman OpenCV-objektin ilmaisimen kouluttaminen ja testaaminen : Osa 5
7. kuvantunnistus syväoppimisen avulla : Osa 6
   • Introduction to Neural Networks
   • Understanding Feedforward Neural Networks
   • Image Recognition using Convolutional Neural Networks
8. objektin havaitseminen syväoppimisen avulla: osa 7

moni asia näyttää vaikealta ja salaperäiseltä. Mutta kun käytät aikaa niiden purkamiseen, arvoitus vaihtuu mestaruuteen, ja sitä me haluamme. Jos olet aloittelija ja havaitset Tietokonenäön kovaksi ja salaperäiseksi, muista vain seuraava

Q : miten syöt norsua ?
A : Yksi puraisu kerrallaan!

mikä on Ominaisuuskuvain?

ominaisuuskuvain on kuvan esitys tai kuvapäivitys, joka yksinkertaistaa kuvaa ottamalla talteen hyödyllistä tietoa ja heittämällä pois epäolennaista tietoa.

tyypillisesti ominaisuuskuvaus muuntaa kuvan, jonka koko on Leveys x Korkeus x 3 (kanavat), ominaisuusvektoriksi / – ryhmäksi, jonka pituus on n. HOG-ominaisuuskuvauksen tapauksessa syötekuva on kooltaan 64 x 128 x 3 ja ulostulon ominaisuusvektori on pituudeltaan 3780.

muista, että HOG descriptor voidaan laskea muillekin kokoluokille, mutta tässä kirjoituksessa pysyn alkuperäisessä paperissa esitetyissä numeroissa, joten voit helposti ymmärtää käsitteen yhdellä konkreettisella esimerkillä.

tämä kaikki kuulostaa hyvältä, mutta mikä on ”hyödyllinen” ja mikä ”vieras” ? Määritellä ”hyödyllinen”, meidän täytyy tietää, mitä se” hyödyllinen ” varten ? Ominaisuusvektori ei selvästikään ole hyödyllinen kuvan katselua varten. Mutta, se on erittäin hyödyllinen tehtäviä, kuten kuvantunnistus ja objektin havaitseminen. Näiden algoritmien tuottama ominaisuusvektori, kun se syötetään kuvanluokitusalgoritmeihin, kuten Support Vector Machine (SVM), tuottaa hyviä tuloksia.

mutta millaiset ”ominaisuudet” ovat hyödyllisiä luokittelutehtävissä ? Keskustellaan tästä asiasta esimerkin avulla. Oletetaan, että haluamme rakentaa objektin ilmaisimen, joka havaitsee paitojen ja takkien napit.

nappi on pyöreä (voi näyttää kuvassa elliptiseltä ) ja siinä on yleensä muutama reikä ompelua varten. Voit ajaa edge detector kuvan painiketta, ja helposti kertoa, jos se on painike yksinkertaisesti katsomalla reunan kuvaa yksin. Tällöin reunatiedot ovat ”hyödyllisiä”ja väritiedot eivät. Lisäksi ominaisuuksilla pitää olla myös syrjivää voimaa. Esimerkiksi kuvasta poimittujen hyvien ominaisuuksien pitäisi pystyä erottamaan painikkeet muista pyöreistä esineistä, kuten kolikoista ja autonrenkaista.

HOG-ominaisuuskuvauksessa piirteinä käytetään gradienttien suuntien jakaumaa ( histogrammeja) (orientoituja gradientteja). Kuvan gradientit (x – ja y-johdannaiset ) ovat hyödyllisiä, koska gradienttien suuruus on suuri reunojen ja kulmien ympärillä ( äkillisten intensiteettimuutosten alueet) ja tiedämme, että reunat ja kulmat sisältävät paljon enemmän tietoa kohteen muodosta kuin tasaiset alueet.

miten orientoitujen gradienttien Histogrammi lasketaan ?

tässä osiossa käsitellään yksityiskohtaisesti sikojen ominaisuuskuvauksen laskemista. Havainnollistaa jokaisen vaiheen, käytämme laastari kuvan.

Vaihe 1 : Esikäsittely

kuten aiemmin mainittiin, jalankulkijoiden tunnistamiseen käytetty Hog-ominaisuuskuvauslaite lasketaan 64×128 kuvan paikkakunnalle. Kuva voi tietysti olla minkä kokoinen tahansa. Tyypillisesti useiden asteikkojen laikkuja analysoidaan monissa kuvapaikoissa. Ainoa rajoite on, että analysoitavilla laastareilla on kiinteä kuvasuhde. Meidän tapauksessamme laastareiden kuvasuhteen on oltava 1: 2. Ne voivat olla esimerkiksi 100×200, 128×256 tai 1000×2000 mutta eivät 101×205.

tämän kohdan havainnollistamiseksi olen esittänyt suuren kuvan, jonka koko on 720×475. Olemme valinneet korjaustiedoston, jonka koko on 100×200, HOG-ominaisuuskuvauksen laskemista varten. Tämä laastari on rajattu pois kuvasta ja kokoa on muutettu 64×128: aan. Nyt olemme valmiita laskemaan HOG kuvaaja tämän kuvan laastari.

dalalin ja Triggsin paperissa mainitaan myös gammakorjaus esikäsittelyvaiheena, mutta suoritusvoitot ovat vähäisiä, joten ohitamme vaiheen.

Vaihe 2: Laske Gradienttikuvat

sian kuvaajan laskemiseksi on ensin laskettava vaaka-ja pystysuuntaiset gradientit; loppujen lopuksi haluamme laskea histogrammi gradientit. Tämä onnistuu helposti suodattamalla kuva seuraavilla ytimillä.

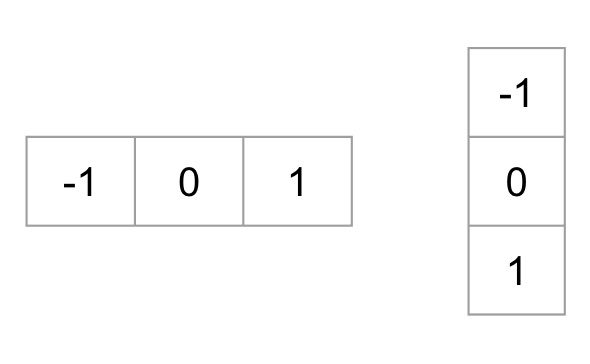
samoihin tuloksiin päästään myös käyttämällä Sobel-operaattoria OpenCV: ssä, jonka ytimen koko on 1.

// C++ gradient calculation.// Read imageMat img = imread("bolt.png");img.convertTo(img, CV_32F, 1/255.0);// Calculate gradients gx, gyMat gx, gy;Sobel(img, gx, CV_32F, 1, 0, 1);Sobel(img, gy, CV_32F, 0, 1, 1);

# Python gradient calculation # Read imageim = cv2.imread('bolt.png')im = np.float32(im) / 255.0# Calculate gradientgx = cv2.Sobel(img, cv2.CV_32F, 1, 0, ksize=1)gy = cv2.Sobel(img, cv2.CV_32F, 0, 1, ksize=1)

seuraavaksi gradientin suuruus ja suunta voidaan löytää seuraavan kaavan avulla

jos käytät OpenCV: tä, laskenta voidaan tehdä funktiolla cartopolar alla esitetyllä tavalla.

// C++ Calculate gradient magnitude and direction (in degrees)Mat mag, angle;cartToPolar(gx, gy, mag, angle, 1);

sama koodi Pythonissa näyttää tältä.

# Python Calculate gradient magnitude and direction ( in degrees )mag, angle = cv2.cartToPolar(gx, gy, angleInDegrees=True)

alla olevassa kuvassa näkyvät kaltevuudet.

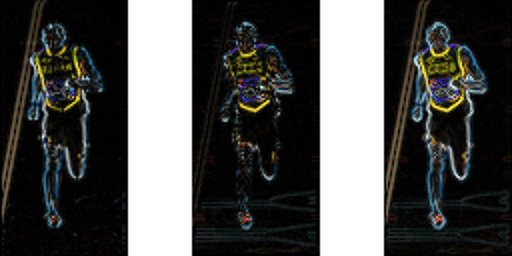
huomaa, että X-gradientti palaa pystyviivoilla ja y-gradientti palaa vaakasuorilla viivoilla. Gradientin suuruus tulipalot missä tahansa on voimakas muutos voimakkuudessa. Mikään niistä ei ammu, kun alue on tasainen. Olen tarkoituksella jättänyt pois kuvan, jossa näkyy gradientin suunta, koska kuvana esitetty suunta ei kerro paljoakaan.

gradienttikuva poisti paljon epäolennaista tietoa (esimerkiksi vakiovärinen tausta ), mutta korosti ääriviivoja. Toisin sanoen voit katsoa gradienttikuvaa ja silti helposti sanoa, että kuvassa on henkilö.

jokaisella pikselillä gradientillä on suuruus ja suunta. Värikuvien osalta arvioidaan kolmen kanavan kaltevuudet (kuten yllä olevassa kuvassa). Gradientin suuruus pikselissä on kolmen kanavan gradienttien suuruuden maksimi ja kulma on suurinta gradienttia vastaava kulma.

Vaihe 3: lasketaan gradienttien Histogrammi 8×8 solussa

tässä vaiheessa kuva jaetaan 8×8 soluun ja kullekin 8×8 solulle lasketaan gradienttien histogrammi.

saamme hetken päästä tietoa histogrammeista, mutta ennen kuin menemme sinne, ymmärtäkäämme ensin, miksi olemme jakaneet kuvan 8×8 soluun. Yksi tärkeä syy käyttää ominaisuuskuvausta kuvan paikkauksen kuvaamiseen on se, että se tarjoaa kompaktin esityksen. 8×8 kuvan paikkaus sisältää 8x8x3 = 192 pikselin arvot. Tämän paikan gradientti sisältää 2 arvoa (suuruus ja suunta ) pikseliä kohti, mikä lisää jopa 8x8x2 = 128 numeroa.

tämän osion loppuun mennessä nähdään, miten nämä 128 lukua esitetään käyttäen 9-bin histogrammia, joka voidaan tallentaa 9 luvun joukkona. Sen lisäksi, että esitys on kompaktimpi, histogrammin laskeminen laastarin päälle tekee tästä repressenaatiosta voimakkaamman kohinalle. Yksittäiset graidents voi olla melua, mutta histogrammi yli 8×8 patch tekee esitys paljon vähemmän herkkä melulle.

mutta miksi 8×8-laastari ? Miksei 32×32 ? Se on suunnitteluvalinta, joka perustuu etsimiemme ominaisuuksien laajuuteen. Hogia käytettiin aluksi jalankulkijoiden tunnistamiseen. 64×128: aan skaalatun jalankulkijan kuvan 8 × 8 solua ovat riittävän suuria vangitsemaan mielenkiintoisia piirteitä (esim.Kasvot, päälaen jne. ).

histogrammi on oleellisesti vektori ( tai jono), jossa on 9 kulmaa (lukua ) vastaava vektori 0, 20, 40, 60 … 160.

Katsotaanpa yhtä 8×8-paikkaista kuvaa ja katsotaan, miltä kaltevuudet näyttävät.

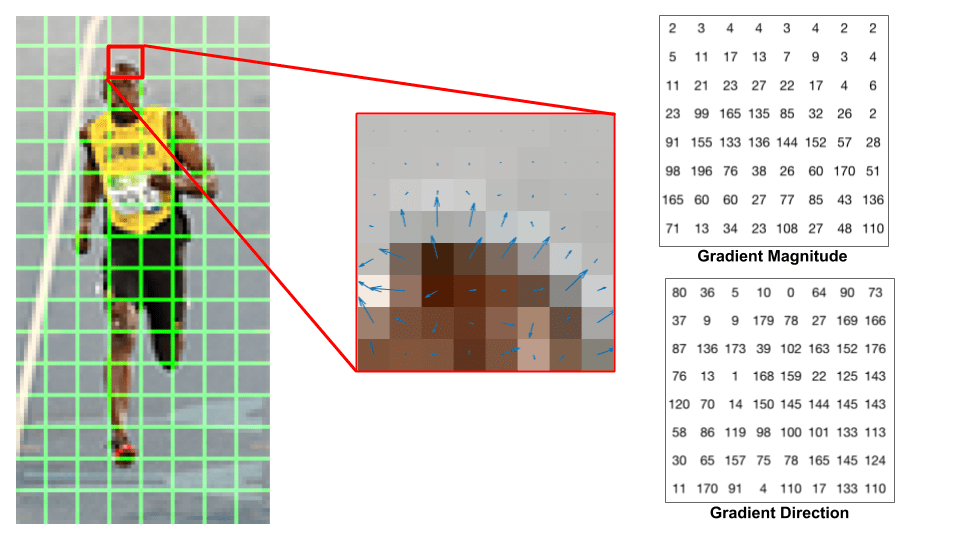
jos olet aloittelija tietokoneen visio, kuva keskellä on hyvin informatiivinen. Se näyttää kuvan laastarin päällekkäin nuolilla, jotka osoittavat gradientin-nuoli näyttää gradientin suunnan ja sen pituus osoittaa magnitudin. Huomaa, miten nuolien suunta osoittaa voimakkuuden muutoksen suuntaan ja suuruus osoittaa, kuinka suuri ero on.

oikealla näkyy raakaluvut, jotka edustavat 8×8-solujen gradientteja yhdellä pienellä erolla-kulmat ovat 0-180 asteen välillä 0-360 asteen sijaan. Näitä kutsutaan” allekirjoittamattomiksi ” gradienteiksi, koska gradientti ja sen negatiivinen esitetään samoilla luvuilla. Toisin sanoen gradienttinuolta ja sitä vastapäätä olevaa 180 astetta pidetään samana. Mutta, miksi ei käytä 0-360 astetta ?

empiirisesti on osoitettu, että allekirjoittamattomat kaltevuudet toimivat paremmin kuin allekirjoitetut kaltevuudet jalankulkijoiden havaitsemiseen. Joissakin Hog-toteutuksissa voit määrittää, haluatko käyttää allekirjoitettuja kaltevuuksia.

seuraava vaihe on luoda histogrammi gradienteista näissä 8×8 solussa. Histogrammissa on 9 laatikkoa, jotka vastaavat kulmia 0, 20, 40 … 160. Seuraava kuva havainnollistaa prosessia. Tarkastelemme saman 8×8-laastarin kaltevuuden suuruutta ja suuntaa kuin edellisessä kuvassa.

bin valitaan suunnan perusteella, ja ääni (arvo, joka menee bin ) valitaan magnitudin perusteella. Keskitytään ensin sinisellä ympäröityyn pikseliin. Sen kulma (suunta ) on 80 astetta ja magnitudi 2. Joten se lisää 2 5. roskakoriin. Redillä ympäröidyn pikselin gradientin kulma on 10 astetta ja magnitudi 4. Koska 10 astetta on puolivälissä välillä 0 ja 20, ääni pikselin jakaantuu tasaisesti kahteen roskakoriin.

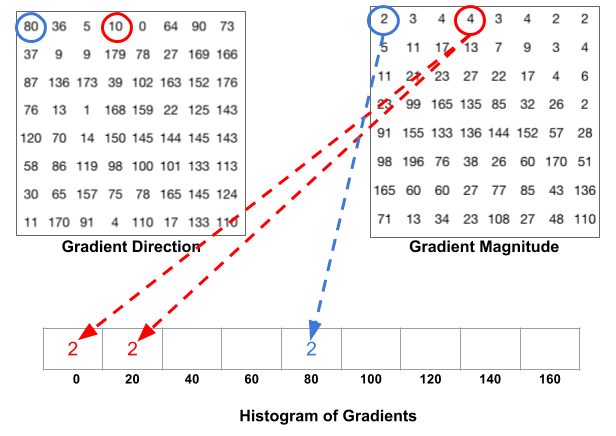
on vielä yksi yksityiskohta. Jos kulma on suurempi kuin 160 astetta, se on välillä 160 ja 180, ja tiedämme kulma kiertyy tekee 0 ja 180 vastaava. Joten alla olevassa esimerkissä pikseli, jonka kulma on 165 astetta, vaikuttaa suhteellisesti 0 asteen bin ja 160 asteen bin.

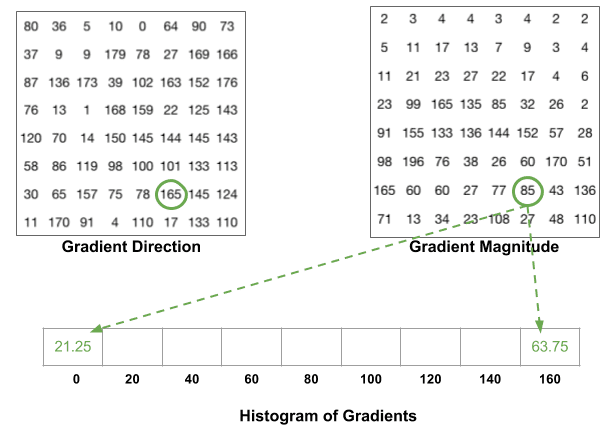
Kaikkien 8×8 solun pikselien osuudet lasketaan yhteen 9-bin histogrammin luomiseksi. Yllä oleva laastari näyttää tältä

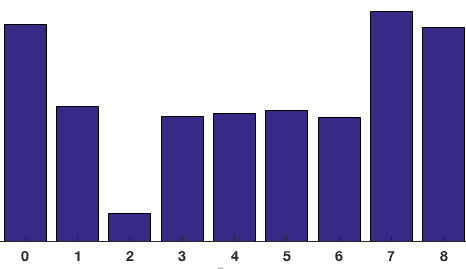
meidän esityksessä y-akseli on 0 astetta. Voit nähdä histogrammi on paljon painoa lähellä 0 ja 180 astetta, mikä on vain yksi tapa sanoa, että laastari kaltevuudet osoittavat joko ylös tai alas.

Vaihe 4 : 16×16 lohkon normalisointi

edellisessä vaiheessa loimme histogrammin kuvan gradientin perusteella. Kuvan kaltevuudet ovat herkkiä kokonaisvalolle. Jos kuvan tekee tummemmaksi jakamalla kaikki pikseliarvot 2: lla, gradientin suuruus muuttuu puolella, ja näin ollen histogrammin arvot muuttuvat puolella.

Ihannetapauksessa haluamme kuvaajamme olevan riippumaton valaistusvaihteluista. Toisin sanoen, haluaisimme ”normalisoida” histogrammi niin ne eivät vaikuta valaistuksen vaihtelut.

ennen kuin selitän, miten histogrammi normalisoituu, katsotaan, miten pituuden 3 vektori normalisoituu.

sanotaan, että meillä on RGB-värivektori . Tämän vektorin pituus on $\sqrt{128^2 + 64^2 + 32^2} = 146.64$. Tätä kutsutaan myös vektorin L2-normiksi. Jakamalla tämän vektorin jokainen alkio luvulla 146,64 saadaan normalisoitu vektori .

tarkastellaan nyt toista vektoria ,jossa alkuaineet ovat kaksi kertaa Ensimmäisen vektorin arvo 2 x=. Voit selvittää sen itse nähdä, että normalisointi johtaa, joka on sama kuin normalisoitu versio alkuperäisen RGB vektori. Vektorin normalisointi poistaa asteikon.

nyt kun osaamme normalisoida vektorin, saatat tuntea kiusausta ajatella, että Hogia laskiessamme voit yksinkertaisesti normalisoida 9×1 histogrammin samalla tavalla kuin normalisoimme yllä olevan 3×1 vektorin. Se ei ole huono idea, mutta parempi idea on normalisoida yli isompi kokoinen lohko 16×16.

16×16-lohkolla on 4 histogrammia, jotka voidaan concatenoida 36 x 1-elementtivektorin muodostamiseksi ja se voidaan normalisoida aivan samalla tavalla kuin 3×1-vektori normalisoidaan. Tämän jälkeen ikkunaa siirretään 8 pikselillä (katso animaatio ) ja tämän ikkunan päälle lasketaan normalisoitu 36×1 vektori ja prosessi toistetaan.

Vaihe 5: laske HOG-ominaisuusvektori

laskeaksesi lopullisen ominaisuusvektorin koko kuvavektorille, 36×1 vektori on kasattu yhdeksi jättiläisvektoriksi. Mikä on tämän vektorin koko ? Lasketaanpa

1. kuinka monta paikkaa 16×16 lohkosta meillä on? Vaaka-ja 15 pystypaikkoja on yhteensä 7 x 15 = 105.
2. jokaista 16×16-lohkoa esittää 36×1-vektori. Joten kun me concatenate ne kaikki yhdeksi gaint vektori saamme 36×105 = 3780 ulotteinen vektori.

orientoitujen gradienttien histogrammin visualisointi

kuvapaikan HOG-kuvaaja visualisoidaan yleensä piirtämällä 9×1 normalisoitua histogrammia 8×8 soluun. Katso kuva sivusta. Huomaat, että hallitseva suunta histogrammi kaappaa muoto henkilö, erityisesti noin vartalon ja jalat.

valitettavasti ei ole helppoa tapaa visualisoida HOG descriptoria OpenCV: ssä.

Tilaa & Latauskoodi