optimaalisen ratkaisun löytäminen tiettyihin optimointiongelmiin voi olla uskomattoman vaikea tehtävä, usein käytännössä mahdotonta. Tämä johtuu siitä, että kun ongelma kasvaa riittävän suureksi, meidän on etsittävä valtava määrä mahdollisia ratkaisuja optimaalisen ratkaisun löytämiseksi. Nykyisellä laskentatehollakin on vielä usein liian monta mahdollista ratkaisua harkittavana. Tässä tapauksessa, koska emme voi realistisesti odottaa löytävämme optimaalista järkevässä ajassa, meidän täytyy tyytyä johonkin, joka on tarpeeksi lähellä.
esimerkki optimointiongelmasta, jossa on yleensä suuri määrä mahdollisia ratkaisuja, olisi kiertävän myyntimiehen ongelma. Jotta löytäisimme ratkaisun esimerkiksi kiertävän myyntimiehen ongelmaan, meidän on käytettävä algoritmia, joka pystyy löytämään riittävän hyvän ratkaisun kohtuullisessa ajassa. Edellisessä opetusohjelmassa tarkastelimme, miten voisimme tehdä tämän geneettisten algoritmien kanssa, ja vaikka geneettiset algoritmit ovat yksi tapa löytää ”tarpeeksi hyvä” ratkaisu kiertävän myyntimiehen ongelmaan, on olemassa muita yksinkertaisempia algoritmeja, joita voimme toteuttaa, joka myös löytää meidät lähelle optimaalista ratkaisua. Tässä opetusohjelma algoritmi käytämme on, ”simuloitu hehkutus”.
jos matkamyyjän ongelma ei ole tuttu, kannattaa ehkä vilkaista edellistä tutoriaaliani ennen jatkamista.
mitä on simuloitu hehkutus?
katsotaan ensin, miten simuloitu hehkutus toimii, ja miksi se on hyvä löytämään ratkaisuja erityisesti kiertävän myyntimiehen ongelmaan. Simuloitu hehkutusalgoritmi sai alkunsa metallityön hehkutusprosessista. Hehkutus liittyy lämmitys ja jäähdytys materiaali muuttaa sen fysikaalisia ominaisuuksia, koska muutokset sen sisäinen rakenne. Metallin jäähtyessä sen Uusi rakenne muuttuu kiinteäksi, mikä saa metallin säilyttämään uudet ominaisuutensa. Simuloidussa hehkutuksessa pidämme lämpötilamuuttujan tämän lämmitysprosessin simuloimiseksi. Asetamme sen aluksi korkealle ja annamme sen sitten hitaasti ”jäähtyä” algoritmin käydessä. Vaikka tämä lämpötilamuuttuja on korkea algoritmi saa, useammalla taajuudella, hyväksyä ratkaisuja, jotka ovat huonompia kuin nykyinen ratkaisu. Tämä antaa algoritmille mahdollisuuden hypätä pois kaikista paikallisista optimumeista, joihin se on joutunut jo varhaisessa vaiheessa suoritusta. Lämpötilan laskiessa on mahdollisuus hyväksyä huonompia ratkaisuja, jolloin algoritmi voi vähitellen keskittyä hakuavaruuden alueelle, jossa toivottavasti on lähellä optimaalista ratkaisua. Tämä asteittainen ”jäähdytys” prosessi tekee simuloitu hehkutus algoritmi huomattavan tehokas löytää lähes optimaalinen ratkaisu käsiteltäessä suuria ongelmia, jotka sisältävät lukuisia paikallisia optimums. Kiertävän myyntimiehen ongelman luonne tekee siitä täydellisen esimerkin.
simuloidun hehkutuksen edut
saatat miettiä, onko simuloidun hehkutuksen toteuttamisesta mitään todellista hyötyä verrattuna yksinkertaiseen mäkikiipeilijään. Vaikka mäkikiipeilijät osaavat yllättävän tehokkaasti löytää hyvän ratkaisun, heillä on myös taipumus juuttua paikallisiin optimumeihin. Kuten aiemmin määritetty, simuloitu hehkutus algoritmi on erinomainen välttää tämän ongelman ja on paljon parempi keskimäärin löytää likimääräinen maailmanlaajuinen optimaalinen.
jotta ymmärtäisimme paremmin, katsotaan nopeasti, miksi mäkikiipeilyn perusalgoritmi on niin altis jäämään kiinni paikallisiin optimumeihin.
mäkikiipeilyalgoritmi yksinkertaisesti hyväksyy naapuriratkaisut, jotka ovat parempia kuin nykyinen ratkaisu. Kun mäkikiipeilijä ei löydä parempia naapureita, se loppuu.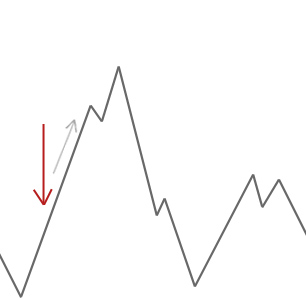
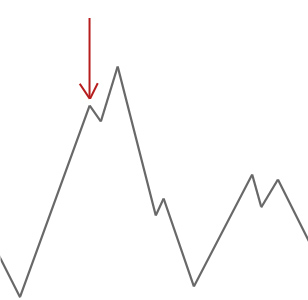
yllä olevassa esimerkissä aloitamme kukkulakiipeilijämme punaisesta nuolesta ja se jatkaa matkaansa mäkeä ylös, kunnes se saavuttaa pisteen, jossa se ei voi kiivetä yhtään korkeammalle laskeutumatta ensin. Tässä esimerkissä näemme selvästi, että se on juuttunut paikalliseen optimiin. Jos tämä olisi todellinen ongelma, emme tietäisi, miltä hakuavaruus näyttää, joten valitettavasti emme pystyisi sanomaan, onko tämä ratkaisu lähelläkään globaalia optimia.
simuloitu hehkutus toimii hieman eri tavalla kuin tämä ja hyväksyy toisinaan huonompia ratkaisuja. Tämä simuloidun hehkutuksen ominaisuus auttaa sitä hyppäämään pois kaikista paikallisista optimumeista, joihin se olisi muuten juuttunut.
Acceptance Function
Let ’ s take a look at how the algorithm decides which solutions to accept so we can better understand how its able to avoid these local optimums.
ensin tarkistetaan, onko naapuriratkaisu nykyistä parempi. Jos on, hyväksymme sen ehdoitta. Jos naapuriratkaisu ei kuitenkaan ole parempi, on otettava huomioon pari tekijää. Ensinnäkin, kuinka paljon huonompi naapuriratkaisu on, ja toiseksi, kuinka korkea järjestelmämme nykyinen ”lämpötila” on. Korkeissa lämpötiloissa järjestelmä todennäköisesti hyväksyä ratkaisuja, jotka ovat huonompia.
tämän matematiikka on melko yksinkertainen:
periaatteessa, mitä pienempi muutos energiassa (liuoksen laatu) ja mitä korkeampi lämpötila, sitä todennäköisemmin algoritmi hyväksyy ratkaisun.
algoritmin yleiskatsaus
joten miltä algoritmi näyttää? No, sen alkeellisin toteutus se on melko yksinkertainen.
- ensin on asetettava alkulämpötila ja luotava satunnainen alkuratkaisu.
- sitten aloitetaan silmukointi, kunnes pysähdysehto täyttyy. Yleensä joko järjestelmä on jäähtynyt riittävästi tai sitten on löydetty riittävän hyvä ratkaisu.
- täältä valitsemme naapurin tekemällä pienen muutoksen nykyiseen ratkaisuumme.
- sen jälkeen päätetään, siirrytäänkö siihen naapuriratkaisuun.
- lopuksi lasketaan lämpötilaa ja jatketaan looppausta
lämpötilan alustus
paremman optimoinnin vuoksi lämpötilamuuttujan alustamisessa tulisi valita lämpötila, joka mahdollistaa aluksi käytännössä kaikki liikkeet nykyistä ratkaisua vastaan. Tämä antaa algoritmille mahdollisuuden tutkia paremmin koko hakutilaa ennen jäähdyttämistä ja asettumista tarkemmalle alueelle.
esimerkkikoodi
nyt käytetään sitä, mitä tiedämme, luodaksemme simuloidun hehkutusalgoritmin ja sovellamme sitä sitten alla olevaan kiertävän myyntimiehen ongelmaan. Aiomme käyttää Java Tässä opetusohjelmassa, mutta logiikan pitäisi toivottavasti olla tarpeeksi yksinkertainen kopioida mille tahansa valitsemallesi kielelle.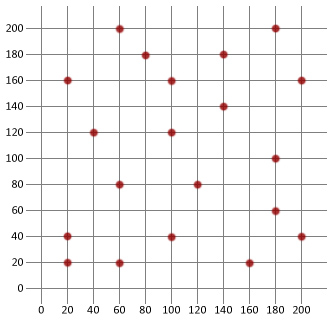
ensin on luotava Kaupunkiluokka, jota voi käyttää mallintamaan matkamyyjän eri kohteita.
Kaupunki.java
* Kaupunki.java
* Models a city
* /
package sa;
public class City {
int x;
int y;
/ / rakentaa satunnaisesti sijoitetun kaupungin
Julkinen Kaupunki () {
tämä.x = (int) (matematiikka.satunnainen ()*200);
tämä.y = (int) (matematiikka.satunnainen()*200);
}
// rakentaa kaupungin valittuun x, Y sijainti
Julkinen Kaupunki (int x, int y){
tämä.x = x;
tämä.y = y;
}
// saa kaupungin x-koordinaatin
public int getX () {
Palauta tämä.x;
}
// saa kaupungin y-koordinaatin
public int getY () {
Palauta tämä.y;
}
// saa etäisyyden annettuun kaupunkiin
public double distanceTo (City city){
int xDistance = Math.abs (getX () – kaupunki.getX());
int yDistance = Math.abs (getY () – kaupunki.getY ());
double distance = Math.sqrt ((xmetäisyys*xmetäisyys) + (yetäisyys*yetäisyys);
paluuetäisyys;
}
@ ohitus
Julkinen Merkkijonotestring () {
return getX ()+”, ” +getY();
}
}
seuraavaksi luodaan luokka, joka voi seurata kaupunkeja.
Turmalaiva.java
* turmakone.java
* pitää hallussaan kiertueen kaupunkeja
* /
package sa;
import java.util.Arraylisti;
public class TourManager {
/ / Holds our cities
private static ArrayList destinationCities = new ArrayList<City>();
// lisää kohdekaupungin
public staattinen void addCity (City city) {
destinationCities.add(kaupunki);
}
// Get a city
public static City getCity (int index){
return (City)destinationCities.get (Hakemisto);
}
// Hae kohdekaupunkien lukumäärä
public staattinen int numerofcities () {
return destinationCities.koko();
}
}
nyt luoda luokan, joka voi mallintaa kiertävä myyntimies kiertue.
kiertue.java
* kiertue.java
* tallentaa ehdokaskierroksen kaikkien kaupunkien kautta
* /
package sa;
import java.util.ArrayList;
tuo java.util.Kokoelmat;
public class Tour{
/ / Holds our tour of cities
private ArrayList tour = new ArrayList<City>();
// Cache
private int distance = 0;
// Constructs a blank tour
public Tour(){
for (int I = 0; i < TourManager.numberOfCities (); i++) {
tour.lisää (null);
}
}
// rakentaa kiertueen toiselta kiertueelta
public Tour (ArrayList tour){
this.tour = (ArrayList) tour.klooni();
}
// Returns tour information
public ArrayList getTour () {
return tour;
}
// luo satunnaisen yksilön
public void generateIndividual () {
// Loop läpi kaikki kohdekaupungit ja lisää ne kiertueeseemme
for (int cityIndex = 0; cityIndex < TourManager.numberOfCities (); cityIndex++) {
setCity (cityIndex, Turmalaiva.getCity(cityIndex));
}
// satunnaisesti uudelleenjärjestellä kiertueen
kokoelmat.shuffle(kiertue;
}
/ / saa kaupungin kiertueelta
public City getCity (int tourbosition) {
return (City)tour.get(turmapaikka);
}
// asettaa Kaupungin tiettyyn asemaan kiertueen sisällä
public void setCity (int tourbosition, City city) {
tour.set (tourPosition, city);
/ / jos kierroksia on muutettu, on palautettava kunto ja etäisyys
etäisyys = 0;
}
// saa kiertueen kokonaisetäisyyden
public int getDistance(){
if (distance == 0) {
int tourDistance = 0;
// Loop through our tour ’ s cities
for (int cityIndex=0; cityIndex < tourSize(); cityIndex++) {
// Get city we ’re traveling from
City fromCity = getCity(cityIndex);
// City we’ re traveling to
City destinationCity;
// Check we ’re not on our tour’ s last city, if we are set our
// tour ’ s final destination city to our starting city
if(cityindex+1 < toursize()){
destinationcity = getcity(cityindex+1);
}
else{
destinationCity = getCity(0);
}
// Hakekaa kahden kaupungin välinen etäisyys
touristance + = fromCity.distanceTo (destinationCity);
}
distance = tourDistance;
}
paluuetäisyys;
}
// Get number of cities on our tour
public int tourSize () {
return tour.koko();
}
@
public String toString () {
String geneString =”|”;
for (int I = 0; i < tourSize (); i++) {
geneString += getCity (i)+”|”;
}
return geneString;
}
}
lopuksi luodaan simuloitu hehkutusalgoritmi.
simuloitu annealing.java
public class Simulated annealing {
/ / Calculate the acceptance probability
public staattinen kaksinkertainen hyväksyttävyyseprobability (int energy, int newEnergy, double temperature) {
/ / If the newenergy is better, accept it
if (newEnergy < energy) {
return 1.0;
}
// jos uusi ratkaisu on huonompi, lasketaan hyväksymistodennäköisyys
paluumatematiikka.exp ((energy-newEnergy)/ temperature);
}
public staattinen void main(String args) {
/ / Create and add our cities
City city = new City(60, 200);
TourManager.addCity (kaupunki;
City city2 = new City (180, 200);
Turmalaiva.addCity (city2);
City city3 = new City(80, 180);
Turmalaiva.addCity (city3);
City city4 = new City (140, 180);
Turmalaiva.addCity (city4);
City city5 = new City (20, 160);
Turmalaiva.addCity (city5);
City city6 = new City(100, 160);
Turmalaiva.addCity (city6);
City city7 = new City (200, 160);
Turmalaiva.addCity (city7);
City city8 = new City (140, 140);
Turmalaiva.addCity (city8);
City city9 = new City (40, 120);
Turmalaiva.addCity (city9);
City city10 = new City (100, 120);
Turmalaiva.addCity(city10);
City city11 = new City (180, 100);
Turmalaiva.addCity(city11);
City city12 = new City (60, 80);
Turmalaiva.addCity(city12);
City city13 = new City (120, 80);
Turmalaiva.addCity(city13);
City city14 = new City (180, 60);
Turmalaiva.addCity(city14);
City city15 = new City (20, 40);
Turmalaiva.addCity(city15);
City city16 = new City (100, 40);
Turmalaiva.addCity(city16);
City city17 = new City (200, 40);
Turmalaiva.addCity (city17);
City city18 = new City (20, 20);
Turmalaiva.addCity(city18);
City city19 = new City (60, 20);
Turmalaiva.addCity(city19);
City city20 = new City (160, 20);
Turmalaiva.addCity (city20);
// Set initial temp
double temp = 10000;
// Cooling rate
double coolingRate = 0.003;
// Initial solution
Tour currentSolution = new Tour ();
currentSolution.generateIndividual ();
järjestelmä.ulos.println (”Initial solution distance:” + currentSolution.getDistance ());
// Set as current best
Tour best = new Tour (currentSolution.getTour ());
// silmukka kunnes järjestelmä on jäähtynyt
kun (temp > 1) {
// Create new neighbour tour
Tour newSolution = new Tour (currentSolution.getTour ());
// saada satunnaisia sijoituksia kiertueella
int tourbos1 = (int) (newSolution.tourSize () * matematiikka.random ());
int tourbos2 = (int) (newSolution.tourSize () * matematiikka.random ());
// Get the cities in selected positions in the tour
City citySwap1 = newSolution.getCity (tourbos1);
City citySwap2 = newSolution.getCity (tourbos2);
// Swap them
newSolution.setCity (tourbos2, citySwap1);
newSolution.setCity (tourbos1, citySwap2);
// Get energy of solutions
int currentEnergy = currentSolution.getDistance ();
int weighourenergy = newSolution.getDistance ();
// Decide if we should accept the neighbour
if(acceptanceProbability (currentEnergy, naapurienergy, temp) > Math.random ()) {
currentSolution = new Tour (newSolution.getTour());
}
// Pidä kirjaa parhaasta löydetystä ratkaisusta
if (currentSolution.getDistance () < best.getDistance ()) {
best = new Tour (currentSolution.getTour());
}
// jäähdytysjärjestelmä
temp *= 1-jäähdytysnopeus;
}
systeemi.ulos.println (”lopullinen ratkaisuetäisyys:” + paras.getDistance ());
järjestelmä.ulos.println (”Tour:” + paras);
}
}
Lähtö
lopullinen ratkaisumatka: 911
kierros: |180, 200/200, 160/140, 140/180, 100/180, 60/200, 40/160, 20/120, 80/100, 40/60, 20/20, 20/20, 40/60, 80/100, 120/40, 120/20, 160/60, 200/80, 180/100, 160/140, 180|
johtopäätös
tässä esimerkissä pystyimme yli puoleen alkuperäisestä satunnaisesti luodusta reitistämme. Tämä toivottavasti osoittaa, kuinka kätevä tämä suhteellisen yksinkertainen algoritmi on, kun sitä sovelletaan tietyntyyppisiin optimointiongelmiin.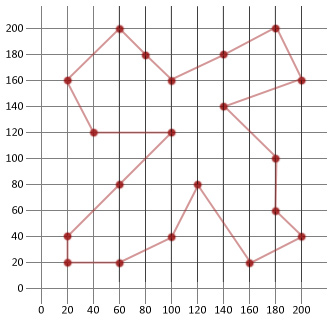
tekijä
 Hello, I ’ m Lee.
Hello, I ’ m Lee.olen Brittiläinen kehittäjä, joka rakastaa teknologiaa ja bisnestä. Täältä löydät artikkeleita ja opetusohjelmia asioista, jotka kiinnostavat minua. If you want to hire me or know more about me head over to my about me page