Le SSIM a été introduit pour la première fois dans l’article de l’IEEE de 2004, Image Quality Assessment: From Error Visibility to Structural Similarity. Le résumé fournit une bonne intuition dans l’idée derrière le système proposé,
Des méthodes objectives d’évaluation de la qualité de l’image perceptuelle ont traditionnellement tenté de quantifier la visibilité des erreurs (différences) entre une image déformée et une image de référence en utilisant une variété de propriétés connues du système visuel humain. En supposant que la perception visuelle humaine est hautement adaptée pour extraire des informations structurelles d’une scène, nous introduisons un cadre complémentaire alternatif pour l’évaluation de la qualité basée sur la dégradation des informations structurelles.
Résumé : Les auteurs font 2 points essentiels,
- La plupart des techniques d’évaluation de la qualité d’image reposent sur la quantification des erreurs entre une référence et un échantillon d’image. Une métrique courante consiste à quantifier la différence des valeurs de chacun des pixels correspondants entre l’échantillon et les images de référence (en utilisant par example l’Erreur Quadratique Moyenne).
- Le système de perception visuelle humaine est hautement capable d’identifier des informations structurelles à partir d’une scène et, par conséquent, d’identifier les différences entre les informations extraites d’une scène de référence et d’une scène d’échantillon. Par conséquent, une métrique qui réplique ce comportement fonctionnera mieux sur les tâches qui impliquent la différenciation entre un échantillon et une image de référence.
La métrique SSIM (Structural Similarity Index) extrait 3 caractéristiques clés d’une image:
- Luminance
- Contraste
- Structure
La comparaison entre les deux images est effectuée sur la base de ces 3 caractéristiques.
La figure 1 ci-dessous montre la disposition et l’écoulement du système de mesure de similarité structurelle. Le Signal X et le Signal Y se réfèrent aux Images de Référence et d’échantillon.

Mais que calcule cette métrique?
Ce système calcule l’Indice de Similarité Structurelle entre 2 images données qui est une valeur comprise entre -1 et +1. Une valeur de +1 indique que les 2 images données sont très similaires ou identiques tandis qu’une valeur de -1 indique que les 2 images données sont très différentes. Souvent, ces valeurs sont ajustées pour être dans la plage, où les extrêmes ont la même signification.
Maintenant, explorons brièvement comment ces caractéristiques sont représentées mathématiquement et comment elles contribuent au score SSIM final.
- Luminance : La luminance est mesurée en faisant la moyenne de toutes les valeurs de pixels. Il est noté μ (Mu) et la formule est donnée ci-dessous,
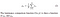
- Contraste: Il est mesuré en prenant l’écart-type (racine carrée de variance) de toutes les valeurs de pixels. Il est noté σ (sigma) et représenté par la formule ci-dessous,
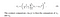
- Structure: La comparaison structurelle se fait en utilisant une formule consolidée (plus à ce sujet plus loin), mais en substance, nous divisons le signal d’entrée avec son écart-type de sorte que le résultat ait un écart-type unitaire, ce qui permet une comparaison plus robuste.
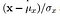
Alors maintenant nous avons établi l’intuition mathématique derrière les trois paramètres. Mais attendez! Nous n’en avons pas encore fini avec le calcul, un peu plus. Ce qui nous manque maintenant, ce sont des fonctions de comparaison qui peuvent comparer les deux images données sur ces paramètres, et enfin, une fonction de combinaison qui les combine toutes. Ici, nous définissons les fonctions de comparaison et enfin la fonction de combinaison qui donne la valeur d’indice de similarité
- Fonction de comparaison de luminance : Elle est définie par une fonction, l(x, y) qui est illustrée ci-dessous. μ(mu) représente la moyenne d’une image donnée. x et y sont les deux images comparées.
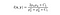
où C1 est une constante pour assurer la stabilité lorsque le dénominateur devient 0. C1 est donné par,
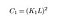
Mise à jour: Tout au long de l’article, nous n’avions pas exploré ce que sont les constantes K et L de cette équation. Heureusement, un lecteur l’a souligné dans les commentaires, et donc dans l’intérêt de rendre cet article un peu plus utile, je vais simplement les définir ici.
L est la plage dynamique pour les valeurs de pixels (nous la définissons comme 255 car nous avons affaire à des images 8 bits standard). Vous pouvez en savoir plus sur quels sont les différents types d’images et ce qu’ils signifient, ici.
K1, K2 sont juste des constantes normales, rien de grand là!
- Fonction de comparaison de contraste : Elle est définie par une fonction c(x, y) qui est illustrée ci-dessous. σ désigne l’écart type d’une image donnée. x et y sont les deux images comparées.
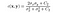
où C2 est donné par,
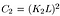
- Fonction de comparaison de structure : Elle est définie par la fonction s(x, y) qui est illustrée ci-dessous. σ désigne l’écart type d’une image donnée. x et y sont les deux images comparées.
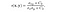
où σ(xy) est défini comme,
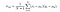
Et enfin, le score SSIM est donné par,

où α > 0, β > 0, γ > 0 désignent l’importance relative de chacune des métriques. Pour simplifier l’expression, si l’on suppose, α = β = γ=1 et C3 = C2/2, on peut obtenir,
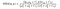
Mais il y a une torsion de l’intrigue!
Bien que vous puissiez implémenter SSIM en utilisant les formules ci-dessus, il est probable qu’il ne sera pas aussi bon que les implémentations prêtes à l’emploi disponibles, comme l’expliquent les auteurs,
Pour l’évaluation de la qualité de l’image, il est utile d’appliquer l’indice SSIM localement plutôt que globalement. Premièrement, les caractéristiques statistiques de l’image sont généralement très non stationnaires spatialement. Deuxièmement, les distorsions d’image, qui peuvent ou non dépendre des statistiques d’image locales, peuvent également être des variantes d’espace. Troisièmement, à des distances de vision typiques, seule une zone locale de l’image peut être perçue avec une résolution élevée par l’observateur humain à un moment donné (en raison de la caractéristique de fovéation du HVS). Enfin, une mesure de qualité localisée peut fournir une carte de qualité variable spatialement de l’image, ce qui fournit plus d’informations sur la dégradation de la qualité de l’image et peut être utile dans certaines applications.
Résumé: Au lieu d’appliquer les mesures ci-dessus globalement (c’est-à-dire sur toute l’image à la fois), il est préférable d’appliquer les mesures au niveau régional (c’est-à-dire dans de petites sections de l’image et en prenant la moyenne globale).
Cette méthode est souvent appelée Indice de similarité structurelle moyen.
En raison de ce changement d’approche, nos formules méritent également des modifications pour refléter la même chose (il est à noter que cette approche est plus courante et sera utilisée pour expliquer le code).
(Remarque: Si le contenu ci-dessous semble un peu accablant, pas de soucis! Si vous en comprenez l’essentiel, alors parcourir le code vous donnera une idée beaucoup plus claire.)
Les auteurs utilisent une fonction de pesée gaussienne symétrique circulaire 11×11 (essentiellement une matrice 11×11 dont les valeurs sont dérivées d’une distribution gaussienne) qui se déplace pixel par pixel sur toute l’image. À chaque étape, les statistiques locales et l’indice SSIM sont calculés dans la fenêtre locale. Puisque nous calculons maintenant les métriques localement, nos formules sont révisées comme suit,
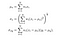
Où wi est la fonction de pondération gaussienne.
Si vous avez trouvé cela un peu peu intuitif, pas de soucis! Il suffit d’imaginer wi comme un multiplicande utilisé pour calculer les valeurs requises à l’aide de quelques astuces mathématiques.
Une fois les calculs effectués sur toute l’image, nous prenons simplement la moyenne de toutes les valeurs SSIM locales et arrivons à la valeur SSIM globale.
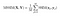
Enfin fini la théorie! Maintenant sur le code!