Apprendre OpenCV

Dans cet article, nous allons apprendre les détails du descripteur de caractéristique de l’Histogramme des gradients orientés (HOG). Nous allons apprendre ce qui se trouve sous le capot et comment ce descripteur est calculé en interne par OpenCV, MATLAB et d’autres paquets.

Cet article fait partie d’une série que j’écris sur la Reconnaissance d’Images et la Détection d’Objets.

La liste complète des tutoriels de cette série est donnée ci-dessous:

1. Reconnaissance d’images à l’aide de techniques traditionnelles de vision par ordinateur : Partie 1
2. Histogramme des Gradients orientés: Partie 2
3. Exemple de code pour la reconnaissance d’images: Partie 3
4. Formation d’un meilleur détecteur oculaire: Partie 4a
5. Détection d’objets à l’aide de techniques traditionnelles de vision par ordinateur: Partie 4b
6. Comment former et tester votre propre détecteur d’objets OpenCV: Partie 5
7. Reconnaissance d’image à l’aide de l’apprentissage en Profondeur : Partie 6
   • Introduction aux Réseaux de Neurones
   • Comprendre les Réseaux de Neurones à Réaction
   • Reconnaissance d’images à l’aide de Réseaux de neurones Convolutifs
8. Détection d’objets à l’aide de l’apprentissage profond : Partie 7

Beaucoup de choses semblent difficiles et mystérieuses. Mais une fois que vous prenez le temps de les déconstruire, le mystère est remplacé par la maîtrise et c’est ce que nous recherchons. Si vous êtes un débutant et que vous trouvez la vision par ordinateur difficile et mystérieuse, rappelez-vous simplement ce qui suit

Q: Comment mangez-vous un éléphant?
A : Une bouchée à la fois !

Qu’est-ce qu’un descripteur d’entités ?

Un descripteur d’entité est une représentation d’une image ou d’un patch d’image qui simplifie l’image en extrayant des informations utiles et en jetant des informations étrangères.

Typiquement, un descripteur d’entités convertit une image de taille largeur x hauteur x 3 (canaux) en un vecteur/tableau d’entités de longueur n. Dans le cas du descripteur d’entités HOG, l’image d’entrée est de taille 64 x 128 x 3 et le vecteur d’entités de sortie est de longueur 3780.

Gardez à l’esprit que le descripteur de PORC peut être calculé pour d’autres tailles, mais dans cet article, je m’en tiens aux nombres présentés dans le document original afin que vous puissiez facilement comprendre le concept avec un exemple concret.

Tout cela sonne bien, mais qu’est-ce qui est « utile » et qu’est-ce qui est « étranger »? Pour définir « utile », nous devons savoir à quoi sert-il « utile »? De toute évidence, le vecteur d’entités n’est pas utile pour visualiser l’image. Mais, il est très utile pour des tâches telles que la reconnaissance d’images et la détection d’objets. Le vecteur caractéristique produit par ces algorithmes lorsqu’il est introduit dans un algorithme de classification d’image tel que Support Vector Machine (SVM) produit de bons résultats.

Mais, quels types de « fonctionnalités » sont utiles pour les tâches de classification? Discutons de ce point en utilisant un exemple. Supposons que nous souhaitions construire un détecteur d’objets qui détecte les boutons des chemises et des manteaux.

Un bouton est circulaire (peut sembler elliptique dans une image) et comporte généralement quelques trous pour la couture. Vous pouvez exécuter un détecteur de bord sur l’image d’un bouton et dire facilement s’il s’agit d’un bouton en regardant simplement l’image de bord seule. Dans ce cas, les informations de bord sont « utiles » et les informations de couleur ne le sont pas. De plus, les caractéristiques doivent également avoir un pouvoir discriminant. Par exemple, les bonnes caractéristiques extraites d’une image devraient pouvoir faire la différence entre les boutons et d’autres objets circulaires comme les pièces de monnaie et les pneus de voiture.

Dans le descripteur d’entités HOG, la distribution (histogrammes) des directions des gradients (gradients orientés) est utilisée comme entités. Les dégradés (dérivés x et y) d’une image sont utiles car l’amplitude des dégradés est grande autour des bords et des coins (régions de changements brusques d’intensité) et nous savons que les bords et les coins contiennent beaucoup plus d’informations sur la forme de l’objet que les régions plates.

Comment calculer l’histogramme des gradients orientés?

Dans cette section, nous allons entrer dans les détails du calcul du descripteur de caractéristique HOG. Pour illustrer chaque étape, nous utiliserons un patch d’une image.

Étape 1 : Le prétraitement

Comme mentionné précédemment, le descripteur de caractéristique HOG utilisé pour la détection de piétons est calculé sur un patch de 64×128 d’une image. Bien entendu, une image peut être de n’importe quelle taille. Généralement, les correctifs à plusieurs échelles sont analysés à de nombreux emplacements d’image. La seule contrainte est que les patchs analysés ont un rapport d’aspect fixe. Dans notre cas, les patchs doivent avoir un rapport d’aspect de 1: 2. Par exemple, ils peuvent être 100×200, 128×256 ou 1000×2000 mais pas 101×205.

Pour illustrer ce point, j’ai montré une grande image de taille 720×475. Nous avons sélectionné un patch de taille 100×200 pour calculer notre descripteur de caractéristique HOG. Ce correctif est recadré à partir d’une image et redimensionné à 64×128. Nous sommes maintenant prêts à calculer le descripteur HOG pour ce patch d’image.

L’article de Dalal et Triggs mentionne également la correction gamma comme étape de prétraitement, mais les gains de performance sont mineurs et nous sautons donc l’étape.

Étape 2: Calculer les images de gradient

Pour calculer un descripteur HOG, nous devons d’abord calculer les gradients horizontaux et verticaux; après tout, nous voulons calculer l’histogramme des gradients. Ceci est facilement réalisé en filtrant l’image avec les noyaux suivants.

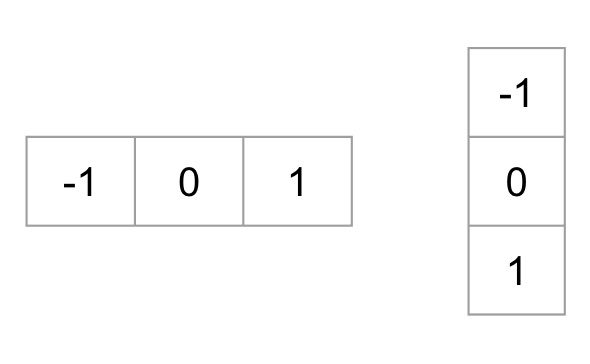
Nous pouvons également obtenir les mêmes résultats, en utilisant l’opérateur Sobel dans OpenCV avec la taille du noyau 1.

// C++ gradient calculation.// Read imageMat img = imread("bolt.png");img.convertTo(img, CV_32F, 1/255.0);// Calculate gradients gx, gyMat gx, gy;Sobel(img, gx, CV_32F, 1, 0, 1);Sobel(img, gy, CV_32F, 0, 1, 1);

# Python gradient calculation # Read imageim = cv2.imread('bolt.png')im = np.float32(im) / 255.0# Calculate gradientgx = cv2.Sobel(img, cv2.CV_32F, 1, 0, ksize=1)gy = cv2.Sobel(img, cv2.CV_32F, 0, 1, ksize=1)

Ensuite, nous pouvons trouver l’amplitude et la direction du gradient en utilisant la formule suivante

Si vous utilisez OpenCV, le calcul peut être effectué à l’aide de la fonction cartToPolar comme indiqué ci-dessous.

// C++ Calculate gradient magnitude and direction (in degrees)Mat mag, angle;cartToPolar(gx, gy, mag, angle, 1);

Le même code en python ressemble à ceci.

# Python Calculate gradient magnitude and direction ( in degrees )mag, angle = cv2.cartToPolar(gx, gy, angleInDegrees=True)

La figure ci-dessous montre les dégradés.

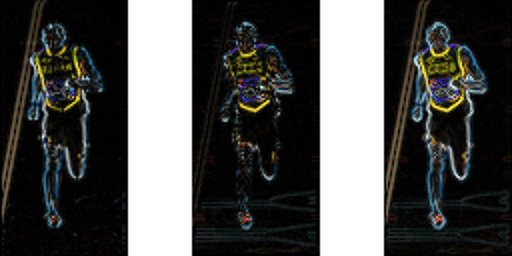
Remarquez, le dégradé x se déclenche sur des lignes verticales et le dégradé y se déclenche sur des lignes horizontales. L’ampleur des incendies de gradient où il y a un changement brusque d’intensité. Aucun d’entre eux ne tire lorsque la région est lisse. J’ai délibérément omis l’image montrant la direction du dégradé car la direction affichée en tant qu’image ne transmet pas beaucoup.

L’image en dégradé a supprimé de nombreuses informations non essentielles (par exemple, un arrière-plan coloré constant), mais a mis en évidence les contours. En d’autres termes, vous pouvez regarder l’image dégradée tout en disant facilement qu’il y a une personne sur l’image.

À chaque pixel, le gradient a une magnitude et une direction. Pour les images en couleur, les dégradés des trois canaux sont évalués (comme indiqué dans la figure ci-dessus). L’amplitude du gradient à un pixel est le maximum de l’amplitude des gradients des trois canaux, et l’angle est l’angle correspondant au gradient maximal.

Étape 3: Calculer l’histogramme des gradients dans 8×8 cellules

Dans cette étape, l’image est divisée en 8×8 cellules et un histogramme de gradients est calculé pour chaque 8×8 cellules.

Nous allons en apprendre davantage sur les histogrammes dans un instant, mais avant d’y aller, comprenons d’abord pourquoi nous avons divisé l’image en cellules 8×8. L’une des raisons importantes d’utiliser un descripteur d’entités pour décrire un patch d’une image est qu’il fournit une représentation compacte. Un patch d’image 8×8 contient des valeurs de 8x8x3 = 192 pixels. Le gradient de ce patch contient 2 valeurs (magnitude et direction) par pixel, ce qui équivaut à 8x8x2 = 128 nombres.

À la fin de cette section, nous verrons comment ces 128 nombres sont représentés à l’aide d’un histogramme à 9 bacs qui peut être stocké sous la forme d’un tableau de 9 nombres. Non seulement la représentation est plus compacte, mais le calcul d’un histogramme sur un patch rend cette représentation plus robuste au bruit. Les graidents individuels peuvent avoir du bruit, mais un histogramme sur un patch 8×8 rend la représentation beaucoup moins sensible au bruit.

Mais pourquoi 8×8 patch? Pourquoi pas 32×32? C’est un choix de conception éclairé par l’échelle des fonctionnalités que nous recherchons. HOG a d’abord été utilisé pour la détection des piétons. les cellules 8×8 d’une photo d’un piéton à l’échelle de 64×128 sont assez grandes pour capturer des caractéristiques intéressantes (par exemple le visage, le haut de la tête, etc. ).

L’histogramme est essentiellement un vecteur (ou un tableau) de 9 cases (nombres) correspondant à des angles 0, 20, 40, 60 … 160.

Regardons un patch 8×8 dans l’image et voyons à quoi ressemblent les dégradés.

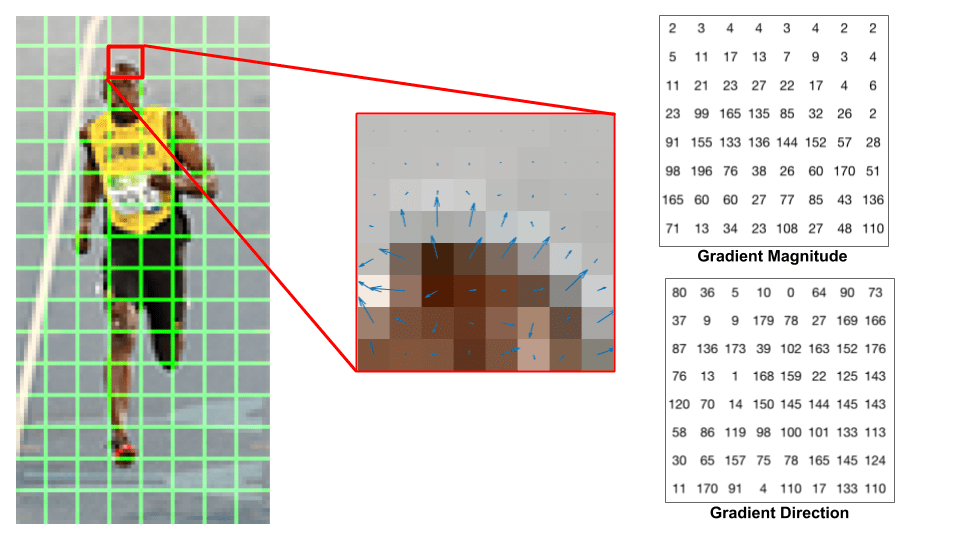
Si vous êtes débutant en vision par ordinateur, l’image au centre est très informative. Il montre le patch de l’image recouvert de flèches montrant le dégradé — la flèche montre la direction du dégradé et sa longueur montre l’ampleur. Remarquez comment la direction des flèches pointe vers la direction du changement d’intensité et la magnitude montre l’ampleur de la différence.

Sur la droite, nous voyons les nombres bruts représentant les gradients dans les cellules 8 ×8 avec une différence mineure — les angles sont compris entre 0 et 180 degrés au lieu de 0 à 360 degrés. Ceux-ci sont appelés gradients « non signés » car un gradient et son négatif sont représentés par les mêmes nombres. En d’autres termes, une flèche de gradient et celle de 180 degrés opposée sont considérées comme identiques. Mais pourquoi ne pas utiliser les degrés 0 – 360?

Empiriquement, il a été démontré que les gradients non signés fonctionnent mieux que les gradients signés pour la détection des piétons. Certaines implémentations de HOG vous permettront de spécifier si vous souhaitez utiliser des dégradés signés.

L’étape suivante consiste à créer un histogramme des gradients dans ces cellules 8×8. L’histogramme contient 9 cases correspondant aux angles 0, 20, 40 … 160. La figure suivante illustre le processus. Nous examinons la magnitude et la direction du gradient du même patch 8× 8 que dans la figure précédente.

Un bac est sélectionné en fonction de la direction, et le vote (la valeur qui entre dans le bac) est sélectionné en fonction de la magnitude. Concentrons-nous d’abord sur le pixel encerclé de bleu. Il a un angle (direction) de 80 degrés et une magnitude de 2. Donc, il ajoute 2 à la 5ème poubelle. Le gradient au pixel encerclé en rouge a un angle de 10 degrés et une magnitude de 4. Puisque 10 degrés est à mi-chemin entre 0 et 20, le vote par le pixel se divise uniformément dans les deux bacs.

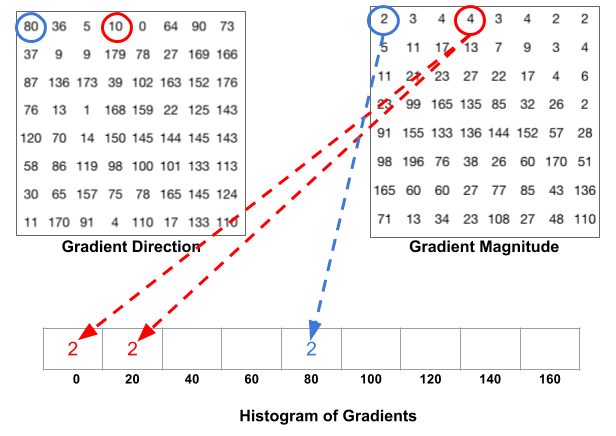
Il y a un détail de plus à connaître. Si l’angle est supérieur à 160 degrés, il est compris entre 160 et 180, et nous savons que l’angle s’enroule autour de ce qui équivaut à 0 et 180. Ainsi, dans l’exemple ci-dessous, le pixel avec un angle de 165 degrés contribue proportionnellement au bac à 0 degré et au bac à 160 degrés.

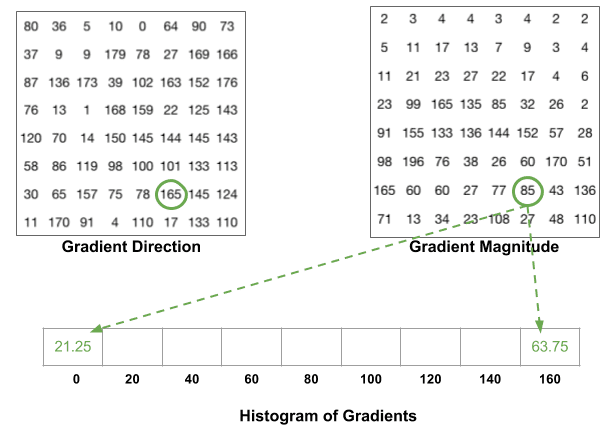
Les contributions de tous les pixels des cellules 8×8 sont additionnées pour créer l’histogramme à 9 cases. Pour le patch ci-dessus, cela ressemble à ceci

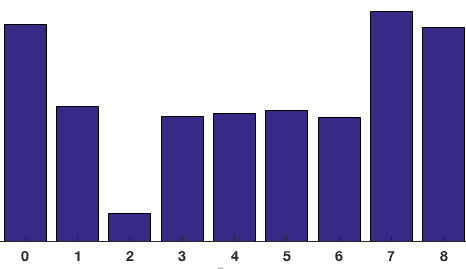
Dans notre représentation, l’axe des ordonnées est de 0 degré. Vous pouvez voir que l’histogramme a beaucoup de poids près de 0 et 180 degrés, ce qui est juste une autre façon de dire que dans le patch, les gradients pointent vers le haut ou vers le bas.

Étape 4 : Normalisation du bloc 16×16

Dans l’étape précédente, nous avons créé un histogramme basé sur le dégradé de l’image. Les dégradés d’une image sont sensibles à l’éclairage général. Si vous assombrissez l’image en divisant toutes les valeurs de pixels par 2, l’amplitude du gradient changera de moitié et, par conséquent, les valeurs de l’histogramme changeront de moitié.

Idéalement, nous voulons que notre descripteur soit indépendant des variations d’éclairage. En d’autres termes, nous aimerions « normaliser » l’histogramme afin qu’ils ne soient pas affectés par les variations d’éclairage.

Avant d’expliquer comment l’histogramme est normalisé, voyons comment un vecteur de longueur 3 est normalisé.

Disons que nous avons un vecteur de couleur RVB. La longueur de ce vecteur est $\sqrt{128^2 + 64^2 + 32^2} = 146.64$. C’est aussi ce qu’on appelle la norme L2 du vecteur. La division de chaque élément de ce vecteur par 146,64 nous donne un vecteur normalisé.

Considérons maintenant un autre vecteur dans lequel les éléments sont deux fois la valeur du premier vecteur 2 x =. Vous pouvez le résoudre vous-même pour voir que la normalisation se traduira par, ce qui est le même que la version normalisée du vecteur RVB d’origine. Vous pouvez voir que la normalisation d’un vecteur supprime l’échelle.

Maintenant que nous savons comment normaliser un vecteur, vous pourriez être tenté de penser que lors du calcul de HOG, vous pouvez simplement normaliser l’histogramme 9 × 1 de la même manière que nous avons normalisé le vecteur 3 × 1 ci-dessus. Ce n’est pas une mauvaise idée, mais une meilleure idée est de normaliser sur un bloc de plus grande taille de 16× 16.

Un bloc 16×16 a 4 histogrammes qui peuvent être concaténés pour former un vecteur de 36 x 1 éléments et il peut être normalisé de la même manière qu’un vecteur 3×1 est normalisé. La fenêtre est alors déplacée de 8 pixels (voir animation) et un vecteur normalisé de 36×1 est calculé sur cette fenêtre et le processus est répété.

Étape 5: Calculer le vecteur caractéristique de PORC

Pour calculer le vecteur caractéristique final pour l’ensemble du patch d’image, les vecteurs 36×1 sont concaténés en un seul vecteur géant. Quelle est la taille de ce vecteur? Calculons

1. Combien de positions des blocs 16×16 avons-nous? Il y a 7 positions horizontales et 15 positions verticales, ce qui fait un total de 7 x 15 = 105 positions.
2. Chaque bloc 16×16 est représenté par un vecteur 36×1. Ainsi, lorsque nous les concaténons tous en un seul vecteur de gaint, nous obtenons un vecteur de dimension 36×105 = 3780.

Visualisation de l’histogramme des Gradients Orientés

Le descripteur HOG d’un patch d’image est généralement visualisé en traçant les histogrammes normalisés 9×1 dans les cellules 8×8. Voir l’image sur le côté. Vous remarquerez que la direction dominante de l’histogramme capture la forme de la personne, en particulier autour du torse et des jambes.

Malheureusement, il n’y a pas de moyen facile de visualiser le descripteur HOG dans OpenCV.

S’abonner & Code de téléchargement