CONDUCTIVITÉ THERMIQUE

La conductivité thermique des solides est de nature différente selon qu’ils sont conducteurs ou non. Dans les diélectriques sans charges électriques libres, l’énergie thermique est transférée par des phonons. Les vibrations collectives des atomes dans le réseau cristallin prennent la forme d’ondes de déplacement dont l’interférence génère des paquets d’ondes, c’est-à-dire des phonons. Les ondes de déplacement provoquent des fluctuations de densité qui peuvent se manifester par une variation d’indice de réfraction. Si les ondes traversent une région dans laquelle l’indice de réfraction diffère de la valeur volumétrique moyenne, les ondes de déplacement ultérieures portant l’énergie du mouvement thermique seront dispersées.

La diffusion est d’autant plus forte que l’écart maximal des atomes par rapport à leurs positions moyennes dans le réseau est élevé, c’est-à-dire que plus le T est élevé. Ceci explique le fait établi expérimentalement que la conductivité thermique des diélectriques cristallins diminue à des températures assez élevées: λ 1/ T (Figure 1).

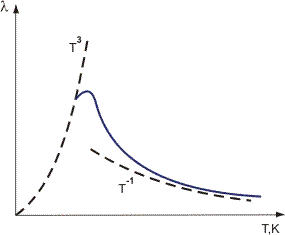
Figure 1. Variation de la conductivité thermique des diélectriques cristallins avec la température.

Debye a donné un aperçu d’un caractère de pointe de la variation λ(T) à bas T dans le cadre des concepts de mécanique quantique. Il a élaboré une théorie dipolaire des diélectriques basée sur le concept d’une molécule en tant que dipôle rigide. Dans ce modèle, Debye a introduit le concept de la température dite de Debye θD proportionnelle à la fréquence maximale des vibrations atomiques dans un solide. Pour la plupart des substances, θD est inférieur ou proche de la température ambiante (une exception est le diamant pour lequel θD = 1850 K et le berrylium pour lequel θD = 1160 K).

Dans la théorie quantique des solides, le réseau cristallin est considéré comme un volume rempli de gaz phononique auquel la déduction de la théorie cinétique la plus simple est appliquée

où c est la capacité thermique d’un diélectrique qui coïncide avec celle du gaz de phonons, v la vitesse moyenne des phonons approximativement égale à la vitesse du son, le libre chemin moyen des phonons. L’existence d’une certaine valeur finie est le résultat de la diffusion de phonons sur les phonons, sur les défauts du réseau cristallin et, en particulier, sur les joints de grains sur l’ensemble de l’échantillon. La dépendance en température λ(T) est déterminée par celle de et c sur la température.

À des températures élevées dépassant sensiblement la température de Debye θD, le mécanisme de base limitant est une diffusion phonon-phonon due à l’anharmonicité des vibrations atomiques dans un cristal. Le mécanisme de résistance thermique phonon-phonon ((1/λ) est connu sous le nom de coefficient de résistance thermique) n’est réalisable que grâce à une transition entraînant un retard du flux de phonons et un changement appréciable du quasi-élan. Plus le T est élevé, plus la probabilité de la transition avec décroissante est élevée:(1/ T). Comme à T > θD la capacité calorifique c n’augmente que légèrement avec la température, d’où λ 1/T.

À des températures inférieures à la température de Debye, T < < θD, la longueur du libre chemin moyen déterminée par la diffusion phonon-phonon croît drastiquement, expθD/T et, en règle générale, est confinée à la taille d’un cristal R. Selon la loi de Debye, la capacité thermique c dans cette plage de températures varie comme c (T/θD) 3. Par conséquent, à T → 0, le coefficient de conductivité thermique λ doit diminuer proportionnellement à T3. La température pour laquelle la conductivité thermique a un pic est déterminée à partir de ≈ R, ce qui correspond généralement à T ≤ 0,05θD.

Cette théorie rend également compte du comportement du coefficient de conductivité thermique pour des substances amorphes n’ayant pas d’ordre à longue portée, c’est-à-dire que la taille de leurs « cristaux » est de l’ordre des tailles atomiques. De ce fait, la diffusion aux « limites » de ces substances doit prévaloir à tous T et ≈ const. Le coefficient de conductivité thermique des substances amorphes λ T3 à basse température et doit croître légèrement, proportionnellement à la capacité thermique, à des températures modérées et élevées, T > θD.

Tout cela fournit une explication qualitative de la dépendance λ(T) dans les diélectriques cristallins réels, mais ne tient pas compte des écarts par rapport au réseau constant dus aux impuretés atomiques d’autres éléments et de leurs propres isotopes. À haute température, la résistance offerte par les impuretés au transport de chaleur est indépendante de la température. Ceci permet d’estimer le degré de pureté du cristal à partir de la variation de sa conductivité thermique avec la température. Le même fait permet de déterminer la répartition entre la substance vitreuse et la substance cristalline dans le minéral naturel si le verre est considéré comme une impureté dans un cristal.

La conductivité thermique des métaux dépend du mouvement et de l’interaction des porteurs de courant, c’est-à-dire des électrons de conduction. Généralement, le coefficient de conductivité thermique λ d’un métal est égal à la somme du réseau (phonon) λph et des composantes de l’électron λe, λ = λe + λph; aux températures ordinaires, en règle générale, λe > > λph.

Si nous appliquons une théorie cinétique simple des gaz au flux d’électrons libres et supposons que la longueur de leur libre trajet ne dépend pas de la vitesse, alors la théorie implique que

où e est la charge électronique, la constante de K Boltzrnann et σ la conductivité électrique. Une théorie mécanique quantique stricte offre une relation similaire,

Dans les deux formules, le rapport de la partie électronique du coefficient de conductivité thermique λ à la conductivité électrique σ, dans une large gamme de températures, semble être proportionnel à la température selon la loi de Wiedemann-Franz, λ/ σ = LT, où L est le nombre de Lorentz. Cette loi est utilisée pour calculer λe à partir de la conductivité électrique mesurée. Cependant, il est violé à des températures inférieures à θD lorsqu’une interaction électron-phonon prévaut (σ croît avec la diminution de T comme T-5 tandis que le varie plus légèrement comme T-2).

Les résultats expérimentaux montrent qu’en règle générale, la conductivité thermique des métaux à haute température est une fonction légèrement décroissante de la température. Mais il existe de nombreuses exceptions. Ainsi, la conductivité thermique du fer diminue fortement avec la température tandis que le tantale et le niobium présentent un coefficient de température positif.

Sont intéressantes les tentatives de comparaison des coefficients de conductivité thermique de différentes substances pour une température caractéristique unique, par exemple pour le point de fusion Tm des solides. Ainsi, le traitement statistique des données expérimentales effectué par Missenard a montré que la conductivité thermique des métaux au point de fusion λ(T = Tm) = λm est proportionnelle à λ et la conductivité thermique des cristaux diélectriques à T = Tm est proportionnelle à , où m est la masse moléculaire, N le nombre d’atomes dans la formule chimique, ρ la densité, et le point de fusion Tm est en Kelvins.

Le transport de chaleur dans les semi-conducteurs est plus complexe que dans les diélectriques et les métaux car le phonon et les composants électroniques sont également essentiels pour eux. Une autre raison de la complexité est l’effet considérable des impuretés, de la diffusion bipolaire et d’autres facteurs peu étudiés sur le transfert de chaleur.

L’effet de la pression sur la conductivité thermique des solides peut être supposé, avec une bonne précision, linéaire, λ pour de nombreux métaux croissant avec p.

Pour l’effet de la porosité sur la conductivité thermique des solides, voir Milieu poreux.