Le champ électrique E peut toujours être exprimé comme le gradient d’une fonction de potentiel scalaire
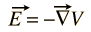
Il n’y a pas de potentiel scalaire général pour le champ magnétique B, mais il peut être exprimé comme la boucle d’une fonction vectorielle
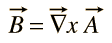
Cette fonction A reçoit le nom de « potentiel vectoriel » mais elle n’est pas directement associée au travail comme l’est le potentiel scalaire.
Le potentiel vectoriel est défini comme étant conforme à la loi d’Ampère et peut être exprimé en termes de courant i ou de densité de courant j (les sources du champ magnétique). Dans divers textes, cette définition prend les formes suivantes
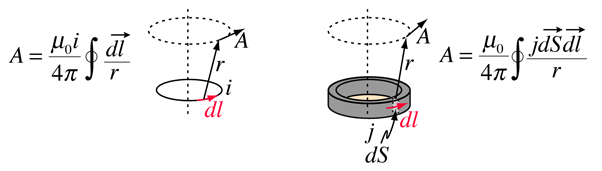
L’une des raisons du potentiel vectoriel est qu’il peut être plus facile de calculer le potentiel vectoriel que de calculer le champ magnétique directement à partir d’une géométrie de courant de source donnée. Son application la plus courante est la théorie des antennes et la description des ondes électromagnétiques.
Puisque le champ magnétique B est défini comme la boucle de A et que l’identité vectorielle de la boucle d’un gradient est identiquement nulle, alors toute fonction arbitraire qui peut être exprimée comme le gradient d’une fonction scalaire peut être ajoutée à A sans changer la valeur de B obtenue à partir de celle-ci. Autrement dit, A ‘ peut être librement substitué à A où
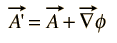
De telles transformations sont appelées transformations de jauge, et il y a eu un certain nombre de « jauges » qui ont été utilisées à l’avantage de types spécifiques de calculs en théorie électromagnétique.