Trouver une solution optimale à certains problèmes d’optimisation peut être une tâche incroyablement difficile, souvent pratiquement impossible. En effet, lorsqu’un problème devient suffisamment important, nous devons rechercher un nombre énorme de solutions possibles pour trouver la solution optimale. Même avec la puissance de calcul moderne, il y a encore souvent trop de solutions possibles à envisager. Dans ce cas, parce que nous ne pouvons pas nous attendre de manière réaliste à trouver l’optimal dans un laps de temps raisonnable, nous devons nous contenter de quelque chose d’assez proche.
Un exemple de problème d’optimisation qui comporte généralement un grand nombre de solutions possibles serait le problème du vendeur itinérant. Afin de trouver une solution à un problème tel que le problème du vendeur itinérant, nous devons utiliser un algorithme capable de trouver une solution suffisante dans un laps de temps raisonnable. Dans un tutoriel précédent, nous avons examiné comment nous pourrions le faire avec des algorithmes génétiques, et bien que les algorithmes génétiques soient un moyen de trouver une solution « assez bonne » au problème du vendeur itinérant, il existe d’autres algorithmes plus simples que nous pouvons implémenter qui nous trouveront également une solution proche de la solution optimale. Dans ce tutoriel, l’algorithme que nous utiliserons est « recuit simulé ».
Si vous n’êtes pas familier avec le problème du vendeur itinérant, il pourrait être utile de jeter un coup d’œil à mon tutoriel précédent avant de continuer.
Qu’est-ce que le recuit simulé?
Tout d’abord, regardons comment fonctionne le recuit simulé et pourquoi il est bon de trouver des solutions au problème du vendeur itinérant en particulier. L’algorithme de recuit simulé a été à l’origine inspiré du processus de recuit dans le travail des métaux. Le recuit consiste à chauffer et à refroidir un matériau pour modifier ses propriétés physiques en raison des changements dans sa structure interne. Au fur et à mesure que le métal refroidit, sa nouvelle structure se fixe, ce qui permet au métal de conserver ses propriétés nouvellement obtenues. Dans le recuit simulé, nous conservons une température variable pour simuler ce processus de chauffage. Nous l’avons initialement réglé haut, puis nous l’avons laissé refroidir lentement au fur et à mesure que l’algorithme s’exécute. Bien que cette variable de température soit élevée, l’algorithme sera autorisé, avec plus de fréquence, à accepter des solutions pires que notre solution actuelle. Cela donne à l’algorithme la possibilité de sauter de tous les optimums locaux dans lesquels il se trouve au début de l’exécution. À mesure que la température diminue, il en va de même des chances d’accepter des solutions pires, permettant ainsi à l’algorithme de se concentrer progressivement sur une zone de l’espace de recherche dans laquelle, espérons-le, une solution proche de l’optimum peut être trouvée. Ce processus de « refroidissement » progressif est ce qui rend l’algorithme de recuit simulé remarquablement efficace pour trouver une solution proche de l’optimum lorsqu’il s’agit de problèmes importants contenant de nombreux optimums locaux. La nature du problème du vendeur itinérant en fait un exemple parfait.
Avantages du recuit simulé
Vous vous demandez peut-être s’il existe un avantage réel à mettre en œuvre un recuit simulé par rapport à quelque chose comme un simple grimpeur. Bien que les grimpeurs puissent être étonnamment efficaces pour trouver une bonne solution, ils ont également tendance à rester coincés dans les optimums locaux. Comme nous l’avons déterminé précédemment, l’algorithme de recuit simulé est excellent pour éviter ce problème et est bien meilleur en moyenne pour trouver un optimum global approximatif.
Pour mieux comprendre, jetons rapidement un coup d’œil à la raison pour laquelle un algorithme d’escalade de colline de base est si enclin à se faire prendre dans des optimums locaux.
Un algorithme de grimpeur acceptera simplement des solutions voisines meilleures que la solution actuelle. Lorsque le grimpeur ne trouve pas de meilleurs voisins, il s’arrête.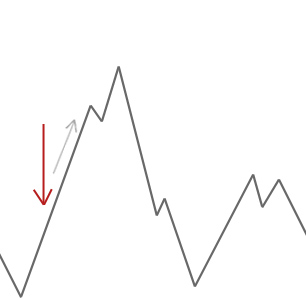
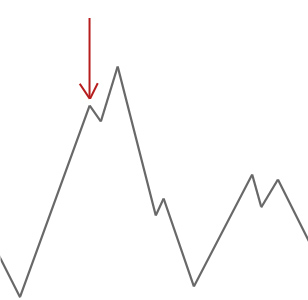
Dans l’exemple ci-dessus, nous commençons notre grimpeur à la flèche rouge et il gravit la colline jusqu’à ce qu’il atteigne un point où il ne peut pas monter plus haut sans descendre d’abord. Dans cet exemple, nous pouvons clairement voir qu’il est coincé dans un optimum local. Si c’était un problème réel, nous ne saurions pas à quoi ressemble l’espace de recherche, nous ne serions malheureusement pas en mesure de dire si cette solution est proche d’un optimum mondial.
Le recuit simulé fonctionne légèrement différemment de celui-ci et accepte parfois des solutions pires. Cette caractéristique du recuit simulé l’aide à sortir de tous les optimums locaux dans lesquels il aurait pu autrement se coincer.
Fonction d’acceptation
Regardons comment l’algorithme décide des solutions à accepter afin de mieux comprendre comment il peut éviter ces optimums locaux.
Nous vérifions d’abord si la solution voisine est meilleure que notre solution actuelle. Si c’est le cas, nous l’acceptons sans condition. Si cependant, la solution voisine n’est pas meilleure, nous devons considérer quelques facteurs. Premièrement, à quel point la solution voisine est pire; et deuxièmement, à quel point la « température » actuelle de notre système est élevée. À des températures élevées, le système est plus susceptible d’accepter des solutions pires.
Le calcul pour cela est assez simple:
Fondamentalement, plus le changement d’énergie (la qualité de la solution) est faible et plus la température est élevée, plus il est probable que l’algorithme accepte la solution.
Aperçu de l’algorithme
Alors, à quoi ressemble l’algorithme? Eh bien, dans sa mise en œuvre la plus basique, c’est assez simple.
- Nous devons d’abord définir la température initiale et créer une solution initiale aléatoire.
- Ensuite, nous commençons à boucler jusqu’à ce que notre condition d’arrêt soit remplie. Habituellement, soit le système a suffisamment refroidi, soit une solution suffisamment bonne a été trouvée.
- De là, nous sélectionnons un voisin en apportant un petit changement à notre solution actuelle.
- Nous décidons ensuite de passer à cette solution voisine.
- Enfin, on diminue la température et on continue à boucler
Initialisation de la température
Pour une meilleure optimisation, lors de l’initialisation de la variable de température, nous devons sélectionner une température qui permettra initialement pratiquement tout mouvement par rapport à la solution actuelle. Cela donne à l’algorithme la possibilité de mieux explorer l’ensemble de l’espace de recherche avant de se refroidir et de s’installer dans une région plus ciblée.
Exemple de code
Utilisons maintenant ce que nous savons pour créer un algorithme de recuit simulé de base, puis appliquons-le au problème du vendeur itinérant ci-dessous. Nous allons utiliser Java dans ce tutoriel, mais la logique devrait être assez simple pour être copiée dans n’importe quelle langue de votre choix.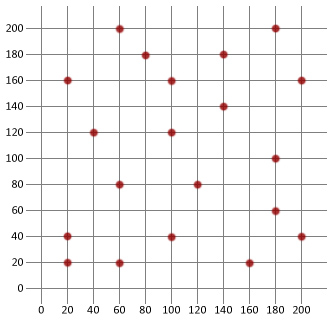
Nous devons d’abord créer une classe de ville qui peut être utilisée pour modéliser les différentes destinations de notre vendeur itinérant.
Ville.java
* Ville.java
* Modèle une ville
* /
paquet sa;
ville de classe publique {
int x;
int y;
// Construit une ville placée au hasard
public City() {
ceci.x = (int) (Math.random() *200);
ceci.y = (int) (Math.au hasard()*200);
}
// Construit une ville à l’emplacement x, y choisi
Ville publique (int x, int y) {
ceci.x = x;
ceci.y = y;
}
// Obtient la coordonnée x de la ville
public int getX() {
renvoie ceci.x;
}
// Obtient la coordonnée y de la ville
public int getY() {
renvoie ceci.d;
}
// Obtient la distance à la ville donnée
public double distanceTo (City city) {
int xDistance=Math.abs(getX() – ville.X());
int yDistance= Math.abs (getY () – ville.getY());
double distance = Math.si vous avez besoin d’une chaîne de caractères publique, vous pouvez utiliser une autre chaîne de caractères, comme la chaîne de caractères, la chaîne de caractères, la chaîne de caractères, la chaîne de caractères, la chaîne de caractères, la chaîne de caractères, la chaîne de caractères, la chaîne de caractères, la chaîne de caractères, la chaîne de caractères, la chaîne de caractères, la chaîne de caractères, la chaîne de caractères, la chaîne de caractères, la chaîne de caractères, la chaîne de caractères, la chaîne de caractères, la chaîne de caractères, la chaîne de caractères, la chaîne de caractères, la chaîne de caractères, la chaîne de caractères, la chaîne de caractères, la chaîne de caractères, la chaîne de caractères, la chaîne de caractères, la chaîne de caractères, la chaîne de caractères.();
}
}
Ensuite, créons une classe qui peut suivre les villes.
TourManager.java
* Gestionnaire de tour.java
* Contient les villes d’un tour
* /
package sa;
import java.util.ArrayList;
TourManager de classe publique {
// Détient nos villes
destination ArrayList statique privée = nouvelle ville ArrayList <>();
// Ajoute une ville de destination
public static void addCity (City city) {
destinationCities.ajouter (ville);
}
// Get a city
ville statique publique getCity(int index) {
destination de retour (Ville) Villes.obtenir (index);
}
// Obtenez le nombre de villes de destination
public static int numberOfCities() {
return destinationCities.taille();
}
}
Maintenant, pour créer la classe qui peut modéliser une visite de vendeur itinérant.
Visite.java
* Visite.java
* Stocke une tournée candidate dans toutes les villes
* /
package sa;
import java.util.ArrayList;
importer java.util.Collections;
Visite de classe publique {
// Organise notre visite des villes
visite privée ArrayList = nouvelle ville ArrayList <>();
// Cache
private int distance = 0;
// Construit un tour vide
public Tour() {
for(int i = 0; i < TourManager.numberOfCities(); i++) {
tour.ajouter (null);
}
}
// Construit une visite à partir d’une autre visite
Visite publique (ArrayList tour) {
ceci.tour = (ArrayList) tour.clone();
}
// Informations sur la visite de retour
public ArrayList getTour() {
visite de retour;
}
// Crée un individu aléatoire
public void generateIndividual() {
// Boucle dans toutes nos villes de destination et les ajoute à notre tour
pour (int cityIndex= 0; cityIndex < TourManager.numberOfCities(); cityIndex++) {
setCity(cityIndex, TourManager.getCity (cityIndex));
}
// Réorganisez aléatoirement les collections de la tournée
.shuffle (tournée);
}
// Obtient une ville de la visite
ville publique getCity(int tourPosition) {
visite de retour (Ville).obtenir (tourPosition);
}
// Définit une ville dans une certaine position au sein d’une visite
public void setCity(int tourPosition, City city) {
visite.set(tourPosition, city);
// Si les tours ont été modifiés, nous devons réinitialiser la condition physique et la distance
distance = 0;
}
// Obtient la distance totale de la visite
public int getDistance() {
if(distance== 0) {
int tourDistance= 0;
// Boucle dans les villes de notre visite
for(int cityIndex=0; cityIndex < tourSize(); cityIndex++) {
// Get city nous voyageons de
City fromCity= getCity(cityIndex);
//City nous voyageons vers
City destinationCity;
// Vérifiez que nous ne sommes pas dans la dernière ville de notre circuit, si nous sommes définis comme la ville de destination finale de notre circuit à notre ville de départ
si ( cityIndex +1 < tourSize()) {
destinationCity =getCity(cityIndex+1);
}
else {
destinationCity=getCity(0);
}
// Obtenez la distance entre les deux villes
tourDistance += fromCity.Distance (destinationCity);
}
distance =tourDistance;
}
distance de retour;
}
// Obtenez le nombre de villes de notre visite
public int tourSize() {
aller-retour.taille();
}
@ J’ai essayé de créer une chaîne de caractères pour la première fois, mais j’ai essayé de la remplacer par une chaîne de caractères publique, comme suit:
Chaîne de caractères publique toString() {
Chaîne de caractères geneString= »| »;
pour (int i= 0; i < tourSize(); i++) {
geneString+= getCity(i)+ »| »;
}
retour geneString;
}
}
Enfin, créons notre algorithme de recuit simulé.
Recuit simulé.paquet java
public class SimulatedAnnealing {
// Calculer la probabilité d’acceptation
public static double acceptanceProbability (int energy, int newEnergy, double temperature) {
// Si la nouvelle solution est meilleure, acceptez-la
if(newEnergy < energy) {
return 1.0;
}
// Si la nouvelle solution est pire, calculez une probabilité d’acceptation
return Math.exp((energy-newEnergy)/temperature);
}
public static void main(String args) {
// Créer et ajouter nos villes
City city= new City(60, 200);
TourManager.addCity (ville);
Ville city2 = nouvelle ville (180, 200);
TourManager.addCity(city2);
City city3 = nouvelle ville(80, 180);
TourManager.addCity(city3);
City city4 = nouvelle ville(140, 180);
TourManager.addCity(city4);
City city5 = nouvelle ville(20, 160);
TourManager.addCity(city5);
City city6 = nouvelle ville(100, 160);
TourManager.addCity(city6);
City city7 = nouvelle ville(200, 160);
TourManager.addCity(city7);
City city8 = nouvelle ville(140, 140);
TourManager.addCity(city8);
City city9 = nouvelle ville(40, 120);
TourManager.addCity (city9);
Ville city10 = nouvelle ville (100, 120);
TourManager.addCity(city10);
City city11 = nouvelle ville(180, 100);
TourManager.addCity(city11);
City city12 = nouvelle ville(60, 80);
TourManager.addCity(city12);
City city13 = nouvelle ville(120, 80);
TourManager.addCity(city13);
City city14 = nouvelle ville(180, 60);
TourManager.addCity(city14);
City city15 = nouvelle ville(20, 40);
TourManager.addCity(city15);
City city16 = nouvelle ville(100, 40);
TourManager.addCity(city16);
City city17 = nouvelle ville(200, 40);
TourManager.addCity (city17);
Ville city18 = nouvelle ville(20, 20);
TourManager.addCity(city18);
City city19 = nouvelle ville(60, 20);
TourManager.addCity(city19);
City city20 = nouvelle ville(160, 20);
TourManager.addCity(city20);
// Définir la température initiale
double température = 10000;
// Taux de refroidissement
double taux de refroidissement = 0,003;
// Initialiser la solution initiale
Tour currentSolution= new Tour();
currentSolution.generateIndividual();
Système.hors.println(« Distance initiale de la solution: » + Solution actuelle.getDistance());
// Définir comme meilleur Tour actuel
meilleur Tour = nouveau Tour (currentSolution.getTour());
// Boucle jusqu’à ce que le système ait refroidi
while(temp > 1) {
// Créer un nouveau tour voisin
Tour newSolution = nouveau tour (currentSolution.getTour());
// Obtenir une position aléatoire dans la tournée
int tourPos1=(int)(newSolution.tourSize() * Math.random());
int tourPos2 =(int)(newSolution.tourSize() * Math.random());
// Obtenez les villes aux positions sélectionnées dans la visite
City citySwap1=newSolution.getCity(tourPos1);
City citySwap2 = newSolution.getCity(tourPos2);
// Échangez-les
newSolution.setCity(tourPos2, citySwap1);
newSolution.setCity(tourPos1, citySwap2);
// Obtenir l’énergie des solutions
int currentEnergy =currentSolution.getDistance();
int Neighborenergy=newSolution.getDistance();
// Décide si nous devons accepter le voisin
if(acceptanceProbability(currentEnergy, Neighborenergy, temp) > Math.random()) {
currentSolution = nouvelle tournée (newSolution.getTour());
}
// Gardez une trace de la meilleure solution trouvée
if (currentSolution.getDistance() < meilleur.getDistance()) {
meilleur = nouvelle tournée (currentSolution.getTour());
}
// Système de refroidissement
temp *= 1 – Taux de refroidissement;
}
Système.hors.println(« Distance de solution finale: » + meilleur.getDistance());
Système.hors.println (« Tour: » + meilleur);
}
}
Sortie
Distance de solution finale: 911
Tour: |180, 200/200, 160/140, 140/180, 100/180, 60/200, 40/160, 20/120, 80/100, 40/60, 20/20, 20/20, 40/60, 80/100, 120/40, 120/20, 160/60, 200/80, 180/100, 160/140, 180|
Conclusion
Dans cet exemple, nous avons pu parcourir plus de la moitié de la distance de notre itinéraire initial généré aléatoirement. Cela montre, espérons-le, à quel point cet algorithme relativement simple est pratique lorsqu’il est appliqué à certains types de problèmes d’optimisation.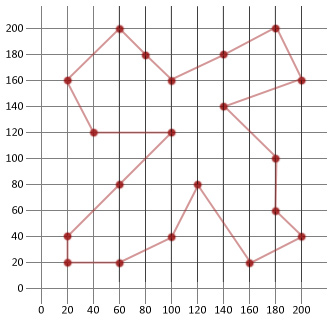
Auteur
 Bonjour, je suis Lee.
Bonjour, je suis Lee.Je suis un développeur britannique qui aime la technologie et les affaires. Vous trouverez ici des articles et des tutoriels sur des choses qui m’intéressent. Si vous voulez m’embaucher ou en savoir plus sur moi, rendez-vous sur ma page à propos de moi