Note de la rédaction: Tony Abbey enseigne des cours de FEA NAFEMS en direct aux États-Unis, en Europe et en Asie. Il enseigne également des cours d’apprentissage en ligne NAFEMS dans le monde entier. Contacter .pour plus de détails.
Un article d’ingénierie de bureau précédent (« Simplify FEA Simulation Models Using Planar Symmetry ») expliquait que même avec des ordinateurs modernes puissants, il y a souvent une motivation à utiliser des techniques de simplification en analyse structurelle par éléments finis (FEA). Ce suivi décrit comment deux méthodes étroitement liées peuvent être utilisées pour prendre des tranches 2D à travers une structure complexe dans des régions d’intérêt. Les modèles FEA qui en résultent peuvent fournir des informations précieuses sur les contraintes locales plus rapidement et plus efficacement qu’un modèle 3D complet. Ils ne raconteront pas toute l’histoire, mais sont des outils précieux pour l’ingénieur CAE.
Les deux méthodes FEA sont appelées contrainte plane et déformation plane. Les deux utilisent des éléments planaires 2D qui ressemblent à des éléments de coque minces et sont maillés à l’aide d’une géométrie de surface plane.
Analyse des contraintes planes
Fig. 1 montre les faits importants sur l’analyse des contraintes planes. La région structurelle est supposée se situer dans le plan 2D xy, la troisième dimension structurelle étant relativement petite. Sur la figure, il s’agit de l’épaisseur dans la direction z. Les contraintes existent dans le plan 2D comme sigma x, sigma y (contraintes directes) et sigma xy (contrainte de cisaillement dans le plan). Chacune de ces contraintes est constante dans l’épaisseur comme indiqué dans l’encart. De plus, il ne peut y avoir aucune contrainte dans la direction z. Cette relation matériau contrainte-déformation est définie dans les éléments de contraintes planes 2D utilisés dans ce type d’analyse.
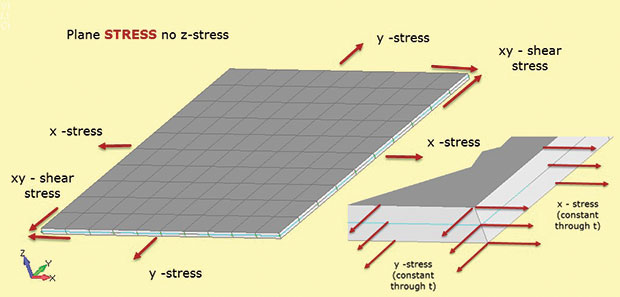Fig. 1: Contrainte plane; hypothèses d’état de contrainte.L’absence de contrainte z est le moyen de se souvenir de la contrainte plane de désignation de type d’élément (c’est-à-dire que seules les contraintes dans le plan sont autorisées). Il n’y a pas non plus de contraintes de cisaillement à travers l’épaisseur. Nous pourrions charger le modèle de contrainte plane de la Fig. 1 avec une charge bi-axiale et calculer sigma x et sigma y. Il n’y a pas de sigma z. Nous pouvons également calculer les contraintes dans le plan correspondantes e-x et e-y. Si nous appliquons une charge de cisaillement, nous pouvons trouver la contrainte de cisaillement sigma xy et la contrainte de cisaillement e-xy. Fait intéressant, nous pouvons également calculer la déformation d’épaisseur traversant e-z. Ce n’est pas nul, car le modèle est libre de s’amincir en z à mesure qu’il s’étire en x et y. Il n’y a pas de contrainte hors plan pour empêcher cela. Dans certains solveurs, nous pouvons récupérer la déformation d’épaisseur traversant e-z et l’utiliser pour calculer le changement d’épaisseur. (Si le modèle est en compression bi-axiale, la section en z deviendra plus épaisse). Ceci est généralement considéré comme une contrainte secondaire et peut ne pas être disponible pour la sortie — mais il est là et peut être calculé manuellement si nécessaire.
Fig. 2 montre un composant de cosse en aluminium. L’ergot fait saillie à partir d’une couche de feuille composite qui a des plis positionnés et collés sur les languettes (ou jambes) et la section inférieure du corps. Les languettes transfèrent la charge appliquée à l’ergot dans la structure composite. En pratique, les nappes seraient étagées pour permettre un transfert de cisaillement en douceur à travers la liaison dans le composite. Le transfert de cisaillement dans le composite est ici simulé par des forces de traction de surface diffuses « tirant » sur les tang. Ceux-ci équilibrent la charge de cosse appliquée.
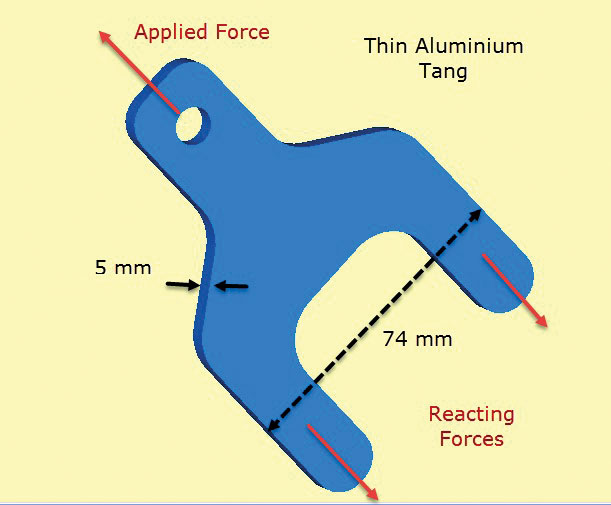Fig. 2: Tang en aluminium à paroi mince transférant la charge dans une structure composite.L’hypothèse clé ici est que les contraintes à travers l’épaisseur sont nulles et que les contraintes dans le plan sont constantes à travers l’épaisseur du composant. Cela signifie que le détail local du transfert de charge de cisaillement du composite au tang est mal modélisé. Cependant, l’objectif de cette analyse est de vérifier le dimensionnement de la section transversale de l’ergot et de la languette à l’écart du composite, en utilisant des contraintes dans le plan.
L’épaisseur du composant est faible par rapport aux autres dimensions. Cette valeur est entrée comme l’épaisseur réelle dans la définition de l’élément de contrainte plane.
Fig. 3 montre le modèle FEA et les contraintes principales maximales calculées. Les zones d’intérêt sont autour de la patte et des rayons de l’épaule. Dans le monde réel, l’état de contrainte aux concentrations de contraintes serait 3D et les contraintes sigma z et les contraintes de cisaillement s’équilibreraient localement. Cependant, il est très raisonnable ici de supposer que les contraintes dans le plan dominent. Il s’agit de la même hypothèse implicite dans la plupart des calculs traditionnels de concentration de contrainte (Kt) que l’on trouve dans les manuels.
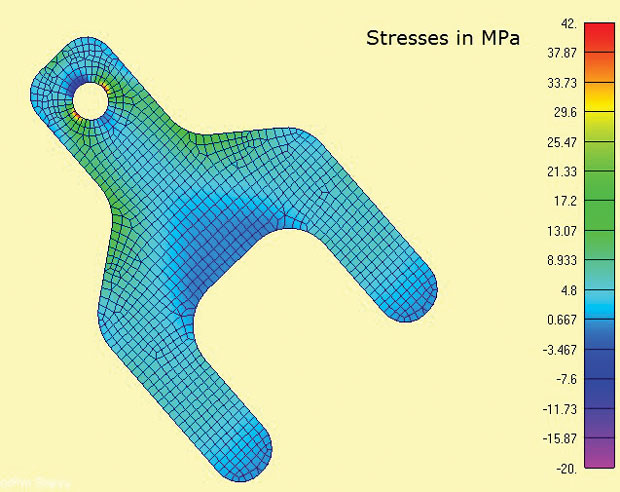Fig 3: Éléments de contraintes planes 2D montrant les contraintes principales maximales L’une des caractéristiques pratiques de l’analyse de contraintes planes est qu’il s’agit d’une analyse strictement 2D, de sorte que seuls trois degrés de liberté (DOF) doivent être contraints (translations dans le plan x, y et rotation autour de l’axe z). Cela se prête à la méthode de contrainte minimale 3-2-1 avec charge équilibrée. Dans un cas 2D, cela dégénère en une méthode 2-1. Un nœud a des contraintes DOF x et y, un deuxième nœud orthogonal approprié a des contraintes DOF x. Cela permet d’appliquer directement la charge de réaction dans les tang sous forme de charges d’équilibrage diffuses. Il serait difficile de simuler cette condition aux limites via des contraintes à la terre.
La déformation e-z de l’épaisseur traversante et donc l’amincissement des tang pourraient être calculés comme un effet secondaire.
Analyse de déformation plane
Fig. 4 montre l’essence de la méthode de déformation plane. Encore une fois, des éléments planaires 2D sont utilisés, mais avec des hypothèses subtilement différentes. Les contraintes dans le plan x, y et xy sont développées comme précédemment. Cependant, cette fois, c’est la déformation hors plan, ou à travers l’épaisseur z, qui est mise à zéro. Ainsi, l’analyse des déformations planes n’autorise que les déformations dans le plan. Cela fonctionne bien pour représenter des structures épaisses telles que montrées. La présence d’une telle quantité de matériau tend à stabiliser le composant et à l’empêcher de s’étirer en z. Cela signifie également que des contraintes constantes d’épaisseur z se développent dans la structure. Cette relation matériau contrainte-déformation est définie dans les éléments de déformation planes 2D utilisés dans ce type d’analyse.
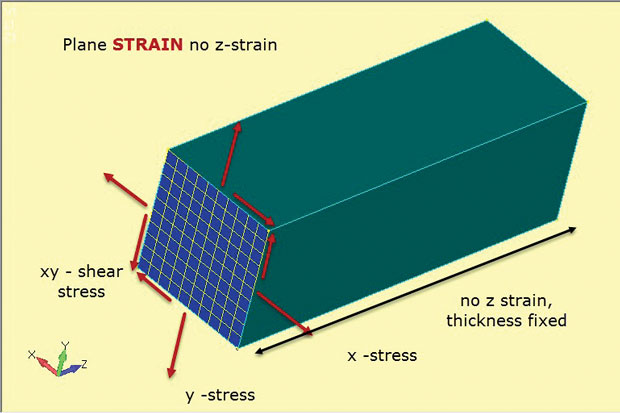Fig. 4: Analyse de déformation plane; hypothèses d’état de contrainte et de déformation.La figure montre l’orientation des éléments de déformation plan 2D sous forme de coupe à travers un composant profond typique. L’hypothèse est que l’état de contrainte à cette section de coupe sera dupliqué à n’importe quelle coupe de plan xy (station z) à travers le composant. Le composant est supposé prismatique (ayant une section transversale constante) sur sa longueur.
En pratique, nous utilisons cette méthode où l’état de contrainte varie lentement d’un plan à l’autre dans un composant profond. Il devrait y avoir suffisamment de matériau à travers la profondeur pour stabiliser et éliminer la déformation d’épaisseur traversante. C’est le même principe utilisé sur les éprouvettes de ténacité à la rupture montrées à la Fig. 5. Une défaillance dans des conditions de déformation plane est indiquée pour la section centrale de l’échantillon épais. La défaillance au niveau des bords libres et de la section mince est un mode différent, plus comme un état de contrainte plane. Un modèle FEA de déformation plane serait par définition une bonne représentation du comportement de l’échantillon épais de l’axe central, mais pas des bords libres ou de l’échantillon mince.
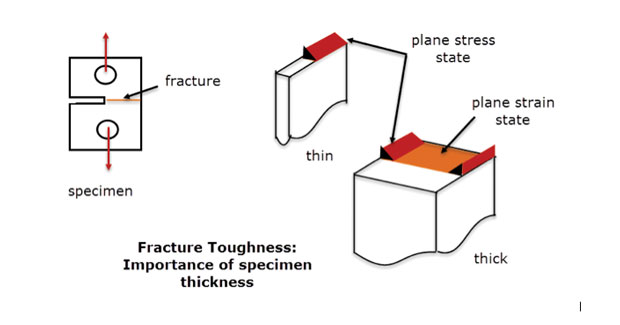Fig. 5: Spécimens de ténacité à la rupture; sections minces et épaisses.Fig. 6 montre un autre composant utilisé dans une structure composite, formant un joint collé. Ici, la section est constante et suffisamment profonde pour que l’on puisse supposer que les contraintes sont également constantes avec la profondeur. Les faces de surface d’extrémité libres (à +z, -z) auront un état de contrainte locale différent (en fait une contrainte plane, comme indiqué), cependant l’objectif de cette analyse est de vérifier les contraintes de section nette sur l’axe (z = 0).
La maille d’analyse de déformation plane 2D est représentée en coupe dans le composant 3D de la Fig. 7. La coupe de section est définie à la station z = 0.
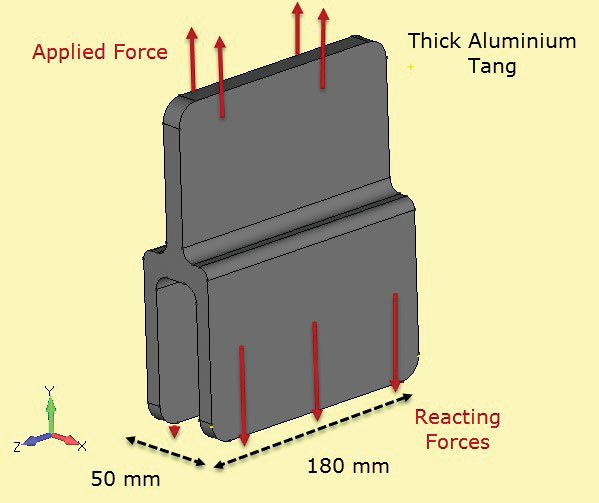Fig 6: Tang d’aluminium à section profonde.
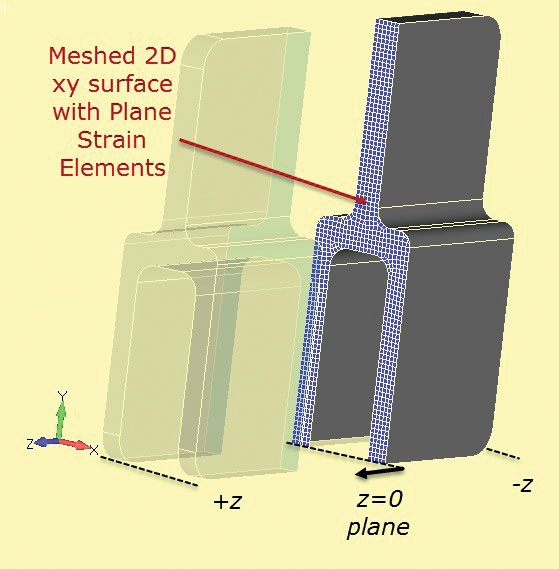Fig. 7: Coupe de section à travers une section solide pour développer une section de déformation plane 2D.Une maille de déformation plane 2D très fine peut être utilisée, qui fonctionnera très rapidement par rapport à un modèle 3D complet. La méthode de contrainte 2-1 est utilisée comme précédemment. Le chargement doit être considéré avec soin. L' »épaisseur » de la section de déformation plane est assez arbitraire et est généralement définie à 1,0 par défaut. Si la charge sur le composant est calculée comme une charge de fonctionnement en profondeur (N /m, Lbf/pouce, etc.) alors cette valeur peut être utilisée directement sur la maille de déformation plane. Il est utile de choisir une section, telle que la seule tang et d’estimer la contrainte nominale ou moyenne dans cette section pour le composant complet. Cela peut être utilisé comme un contrôle de santé mentale dans l’analyse de déformation plane. Un chargement incorrect est probablement la principale cause d’erreur dans cette méthode.
Les résultats de l’analyse sont représentés à la Fig. 8 et montrer clairement les régions de stress élevé autour du filet d’épaule. Les contraintes sont valables pour la région de profondeur centrale du composant (z = 0).
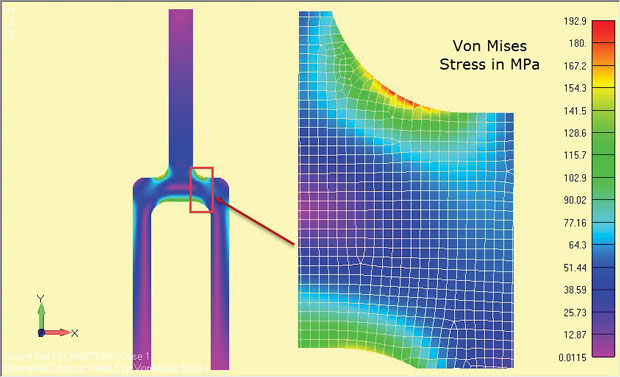Fig. 8: Résultats de l’analyse de déformation plane d’un composant de tang profond.Les quantités de contraintes utilisées dépendront du solveur utilisé. Certains solveurs ignorent les contraintes de direction z comme secondaires et récupèrent les contraintes dans le plan. Les contraintes principales et les contraintes de Von Mises se rapportent alors à un état de contrainte 2D dans le plan. Si la contrainte de direction z est récupérée, elle doit être clairement identifiée, de sorte que l’état de contrainte 2D dans le plan x-y puisse être identifié.
Que représente exactement la contrainte de direction z? C’est la contrainte développée en raison de l’application d’une contrainte de direction z nulle. La contrainte agit comme si les faces d’extrémité libres de la section prismatique étaient fixes. Au niveau du plan central d’un composant de section profonde, ce seront les contraintes complémentaires nécessaires pour maintenir l’état de déformation de direction z nulle. En réalité, à mesure que nous nous dirigeons vers les faces de surface libres, la contrainte z tombe à zéro et devient une distribution de contrainte plane (comme on le voit dans l’échantillon de mécanique des fractures épaisses).
Dans de nombreux cas, tels qu’un cylindre sous pression, les faces d’extrémité sont coiffées et vont en fait développer une contrainte axiale due aux efforts axiaux. Ce sera une contrainte différente de la contrainte axiale induite dans l’analyse de déformation plane. Un calcul manuel sera nécessaire pour calculer les contraintes axiales, ou éventuellement un modèle axisymétrique supplémentaire pour les récipients sous pression.
La facilité de la géométrie et de la construction des mailles se prête bien aux études de simulation ou aux études d’optimisation de formes plus formelles.
À titre de comparaison, une analyse 3D complète en demi-symétrie de la composante tang profonde a été effectuée et les résultats sont présentés à la Fig. 9. La contrainte nominale sur la jambe de tangage unique supérieure est identique dans les deux cas — rappelez-vous que c’est la base de tout contrôle de santé mentale.
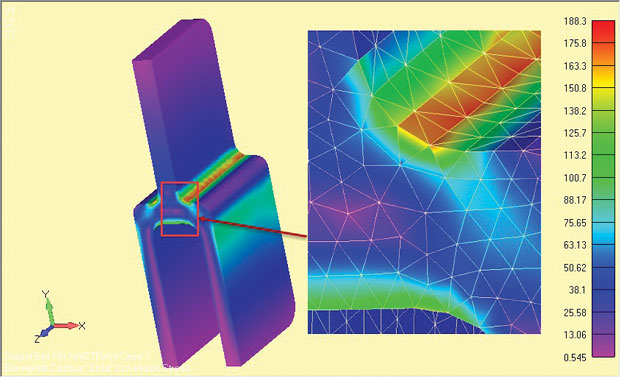Fig. 9: Modèle 3D complet de la saveur profonde, montrant les résultats du stress.Les contraintes d’épaulement locales sont inférieures d’un faible pourcentage dans le modèle complet. C’est pour trois raisons. Premièrement, le maillage tet 3D relativement grossier est inférieur au maillage local de déformation plane 2D très fin. Un contrôle de convergence sur le modèle 3D n’a pas été effectué.
Deuxièmement, il y a un petit changement de géométrie au niveau des surfaces libres (+z, -z) par rapport à la section z = 0 en raison des filets d’extrémité. Dans ce cas, l’effet est négligeable car les filets sont éloignés des régions de l’épaule. Dans de nombreux composants, cependant, il y aura des filets locaux et des détails épuisés. ce qui fera varier la géométrie d’une simple face plane xy. Les variations de contraintes locales sur les faces d’extrémité libres peuvent devoir être estimées ou vérifiées avec un modèle 3D complet.
Enfin, l’hypothèse de déformation plane d’une contrainte z fixe aux sections +z,-z n’est pas vraie pour une composante de profondeur finie. La contrainte z va se diffuser à zéro sur les » vraies » faces libres. Cet effet est représenté à la Fig. 10, qui utilise le modèle 3D tel quel et également comme simulation de la contrainte z de déformation plane.
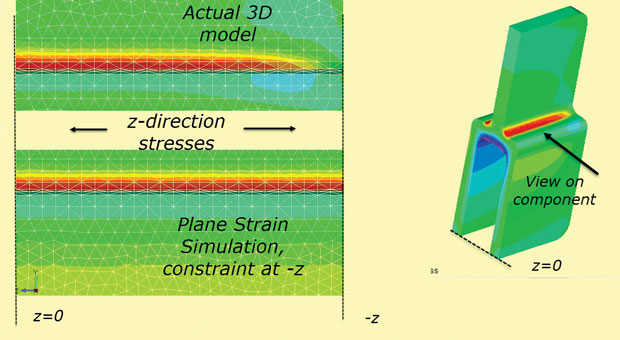Fig. 10 : Diffusion de la contrainte z vers la surface libre.Rapide et efficace
Les analyses de contraintes planes et de contraintes planes sont des méthodes 2D utiles qui peuvent souvent compléter les modèles 3D à grande échelle. Toutes les caractéristiques ne peuvent pas être représentées, mais avec une certaine ingéniosité, les contraintes dans des domaines clés peuvent au moins être estimées. La motivation de l’utilisation des méthodes est de permettre une analyse rapide et efficace avec une géométrie 2D et une construction de maillage faciles.