az SSIM-et először a 2004-es IEEE tanulmányban vezették be, képminőség-értékelés: a hiba láthatóságától a szerkezeti Hasonlóságig. Az absztrakt jó intuíciót nyújt a javasolt rendszer mögött álló ötlethez,
az észlelési képminőség értékelésére szolgáló objektív módszerek hagyományosan megkísérelték számszerűsíteni a torzított kép és a referenciakép közötti hibák (különbségek) láthatóságát az emberi látórendszer számos ismert tulajdonságának felhasználásával. Feltételezve, hogy az emberi vizuális észlelés nagymértékben alkalmazkodik a strukturális információk jelenetből történő kinyeréséhez, bevezetünk egy alternatív kiegészítő keretet a minőségértékeléshez, amely a strukturális információk degradációján alapul.
összefoglaló: a szerzők 2 lényeges pontot tesznek,
- a legtöbb képminőség-értékelési technika a referencia és a mintakép közötti hibák számszerűsítésére támaszkodik. Általános metrika a minta és a referenciaképek közötti megfelelő pixelek értékeinek különbségének számszerűsítése (például az átlagos Négyzethiba használatával).
- az emberi vizuális érzékelési rendszer nagymértékben képes azonosítani a jelenetből származó strukturális információkat, és ezáltal azonosítani a referenciából és a mintából nyert információk közötti különbségeket. Ezért egy olyan mutató, amely megismétli ezt a viselkedést, jobban teljesít azokon a feladatokon, amelyek különbséget tesznek a minta és a referenciakép között.
a strukturális hasonlósági Index (SSIM) metrikus 3 fő jellemzőt von ki egy képből:
- fényerő
- kontraszt
- szerkezet
a két kép összehasonlítása e 3 jellemző alapján történik.
az alábbi 1. ábra a szerkezeti Hasonlóságmérő rendszer elrendezését és áramlását mutatja. Az X jel és az Y jel a referencia-és Mintaképekre vonatkozik.

de mit számít ez a mutató?
ez a rendszer kiszámítja a szerkezeti hasonlósági indexet 2 adott kép között, amely -1 és +1 közötti érték. A + 1 érték azt jelzi, hogy a 2 adott kép nagyon hasonló vagy azonos, míg a -1 érték azt jelzi, hogy a 2 adott kép nagyon eltérő. Ezeket az értékeket gyakran úgy állítják be , hogy a tartományban legyenek, ahol a szélsőségek ugyanazt jelentik.
most nézzük meg röviden, hogyan ábrázolják ezeket a tulajdonságokat matematikailag, és hogyan járulnak hozzá a végső SSIM pontszámhoz.
- fénysűrűség: a fénysűrűséget az összes képpontérték átlagolásával mérik. A képletet pedig az alábbiakban adjuk meg,
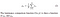
- Kontraszt: Ezt úgy mérjük, hogy az összes pixelérték szórását (a variancia négyzetgyökét) vesszük. Az alábbi képlettel jelöljük (szigma), és az alábbi képlettel jelöljük,
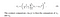
- Szerkezet: A szerkezeti összehasonlítást konszolidált képlet alkalmazásával végezzük (erről később), de lényegében a bemeneti jelet elosztjuk annak szórásával úgy, hogy az eredmény egység szórása legyen, amely robusztusabb összehasonlítást tesz lehetővé.
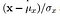
tehát most megállapítottuk a matematikai intuíciót a három paraméter mögött. De tarts ki! Még nem végeztünk a matematikával, még egy kicsit. Ami most hiányzik, azok az összehasonlító funkciók, amelyek összehasonlíthatják a két megadott képet ezeken a paramétereken, végül pedig egy kombinációs funkció, amely egyesíti őket. Itt definiáljuk az összehasonlító függvényeket, végül pedig azt a kombinációs függvényt, amely a
- fénysűrűség-összehasonlító függvényt adja meg: az alább látható L(x, y) függvény határozza meg. a (MU) egy adott kép átlagát jelenti. x és y a két kép összehasonlítása.
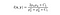
ahol C1 állandó a stabilitás biztosítására, amikor a nevező 0 lesz. A C1-et az adja,
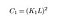
frissítés: a cikk során nem vizsgáltuk meg, hogy mi a K és L állandók ebben az egyenletben. Szerencsére egy olvasó rámutatott erre a megjegyzésekben, ezért annak érdekében, hogy ez a cikk egy kicsit hasznosabb legyen, itt csak meghatározom őket.
L a pixelértékek dinamikus tartománya (255-re állítjuk, mivel standard 8 bites képekkel foglalkozunk). Itt olvashatsz többet arról, hogy mik a különböző képtípusok és mit jelentenek.
K1, K2 csak normális állandók, semmi sok van!
- kontraszt-összehasonlító funkció: az alábbiakban bemutatott C(x, y) függvény határozza meg. egy adott kép szórását jelöli. x és y a két kép összehasonlítása.
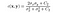
ahol C2 adja meg,
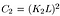
- szerkezet-összehasonlító függvény: az alább látható S(x, y) függvény határozza meg. egy adott kép szórását jelöli. x és y a két kép összehasonlítása.
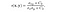
ahol a(Z) (XY) a következőképpen definiálható:,
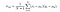
végül az SSIM pontszámot az adja meg,

ahol a > 0, a > 0, a > 0 Az egyes mutatók relatív fontosságát jelöli. A kifejezés egyszerűsítése érdekében, ha feltételezzük, hogy a = = = = = 1 és C3 = C2/2, akkor megkaphatjuk,
de van egy telek csavar!
bár a fenti képletekkel megvalósíthatja az SSIM-t, valószínű, hogy nem lesz olyan jó, mint a rendelkezésre álló használatra kész megvalósítások, mivel a szerzők ezt elmagyarázzák,
a képminőség értékeléséhez hasznos az SSIM indexet lokálisan, nem pedig globálisan alkalmazni. Először is, a képstatisztikai jellemzők általában térben erősen nem helyhez kötöttek. Másodszor, a kép torzulásai, amelyek függhetnek vagy nem függhetnek a helyi képstatisztikától, szintén térváltozatosak lehetnek. Harmadszor, tipikus megtekintési távolságoknál az emberi megfigyelő egyszerre csak a kép helyi területét érzékelheti nagy felbontással (a HVS foveációs jellemzője miatt). Végül, a lokalizált minőségmérés térben változó minőségi térképet adhat a képről, amely több információt szolgáltat a kép minőségromlásáról, és hasznos lehet egyes alkalmazásokban.
összefoglaló: Ahelyett, hogy a fenti mutatókat globálisan (azaz az egész képre egyszerre) alkalmaznánk, jobb, ha a mutatókat regionálisan alkalmazzuk (azaz a kép kis részeiben, és az átlagot vesszük).
ezt a módszert gyakran nevezik átlagos szerkezeti hasonlósági Indexnek.
a megközelítés ezen változása miatt képleteink is megérdemlik a módosításokat, amelyek ugyanezt tükrözik (meg kell jegyezni, hogy ez a megközelítés gyakoribb, és a kód magyarázatára szolgál).
(Megjegyzés: Ha az alábbi tartalom kissé elsöprőnek tűnik, ne aggódjon! Ha megkapja a lényegét, akkor a kód áttekintése sokkal világosabb ötletet ad.)
a szerzők 11×11 körszimmetrikus Gauss-mérési függvényt használnak (alapvetően egy 11×11 mátrixot, amelynek értékei Gauss-eloszlásból származnak), amely pixelről pixelre mozog az egész képen. Minden lépésben a helyi statisztika és az SSIM index a helyi ablakban kerül kiszámításra. Mivel most helyileg számítjuk ki a mutatókat, képleteinket a következőképpen módosítjuk,
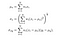
ahol wi a Gauss súlyozási függvény.
ha úgy találta, ez egy kicsit unintuitive, nem gond! Elegendő a wi-t multiplikátorként elképzelniés amelyet a szükséges értékek kiszámításához használnak néhány matematikai trükk segítségével.
miután az egész képen elvégeztük a számításokat, egyszerűen vesszük az összes helyi SSIM érték átlagát, és megkapjuk a globális SSIM értéket.
végre kész az elmélet! Most a kódra!