elkezdtem Andrew Ng népszerű gépi tanulási tanfolyamát a Coursera-n. Az első héten kiterjed egy csomó, legalábbis valaki, aki nem érintette sok kalkulus néhány éve
- költség függvények (átlagos különbség négyzet)
- gradiens Süllyedés
- lineáris regresszió
ez a három téma volt sok, hogy a. Részletesen beszélek mindegyikről, és arról, hogyan illeszkednek egymáshoz, néhány python kóddal.
Szerkesztés május 4-én: Közzétettem egy nyomon követést, amelynek középpontjában a Költségfüggvény működik itt, beleértve az intuíciót, hogyan kell kiszámítani kézzel és két különböző Python implementációt. Meg tudom csinálni a gradiens leereszkedést, majd hamarosan összehozom őket lineáris regresszióhoz.
Modellábrázolás
először is, a legtöbb gépi tanulási algoritmus célja egy modell felépítése: egy hipotézis, amely felhasználható az Y becslésére X alapján. Tegyük fel például, hogy egy olyan modellt képezek ki, amely egy csomó lakásadaton alapul, amely tartalmazza a ház méretét és az eladási árat. A képzés egy modell, tudok adni egy becslést, hogy mennyi lehet eladni a házat, a mérete alapján. Ez egy példa a regressziós problémára — adott bemenet esetén folyamatos kimenetet akarunk megjósolni.
a hipotézist általában a következőképpen mutatják be

a theta értékek a paraméterek.
néhány gyors példa arra, hogyan vizualizáljuk a hipotézist:
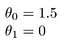
ez H(x) = 1,5 + 0x értéket eredményez. 0x azt jelenti, hogy nincs meredekség, és y mindig az állandó 1,5. Ez úgy néz ki, mint:

mi a helyzet
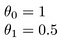

a modell létrehozásának célja olyan paraméterek vagy theta értékek kiválasztása, hogy h(x) közel legyen y-hoz a képzési adatokhoz, x és y. Tehát ezekre az adatokra
x =
y =

megpróbálom megtalálni a legmegfelelőbb vonalat lineáris regresszióval. Lássunk hozzá.
Költségfüggvény
olyan függvényre van szükségünk, amely minimalizálja az adatkészletünk paramétereit. Az egyik gyakori függvény, amelyet gyakran használnak, az átlagos négyzethiba, amely a becslő (az adatkészlet) és a becsült érték (az előrejelzés) közötti különbséget méri. Ez így néz ki:

kiderült, hogy kicsit módosíthatjuk az egyenletet, hogy a számítás egy kicsit egyszerűbb legyen. Mi a végén:
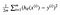
alkalmazzuk ezt a const függvényt a következő adatokra:

most kiszámolunk néhány theta értéket, és kézzel ábrázoljuk a költségfüggvényt. Mivel ez a függvény áthalad (0, 0), csak a theta egyetlen értékét vizsgáljuk. Innentől kezdve a költségfüggvényre hivatkozom, mint J ( ++ ).
J(1) esetén 0-t kapunk. Nem meglepő — a J (1) értéke egyenes vonalat eredményez, amely tökéletesen illeszkedik az adatokhoz. Mi a helyzet a J(0.5)?

az MSE függvény 0,58 értéket ad nekünk. Ábrázoljuk mindkét eddigi értékünket:
J(1) = 0
J (0,5) = 0.58

előre megyek, és kiszámolok még néhány értéket J-ről ( ++ ).

és ha szépen összekapcsoljuk a pontokat…

láthatjuk, hogy a költségfüggvény minimális, ha theta = 1. Ennek van értelme-kezdeti adataink egy egyenes vonal, amelynek lejtése 1 (a fenti ábrán a narancssárga vonal).
gradiens Süllyedés
a fenti próbálkozásokkal minimalizáltuk a J — t ( ++ ) – csak sok értéket próbáltunk ki, és szemrevételeztük az eredményül kapott gráfot. Kell, hogy legyen jobb megoldás? Sor gradiens Süllyedés. A gradiens Süllyedés egy általános funkció a funkció minimalizálására, ebben az esetben az átlagos négyzet Hibaköltség függvény.
a gradiens Süllyedés alapvetően csak azt teszi, amit kézzel csináltunk — apránként változtassa meg a theta értékeket vagy paramétereket, amíg remélhetőleg meg nem érkeztünk a minimumhoz.
azzal kezdjük, hogy inicializáljuk a theta0-t és a theta1-et bármely két értékre, mondjuk mindkettőre 0-t, és onnan indulunk. Formálisan az algoritmus a következő:

ahol az alfa, az a tanulási Arány, vagy az, hogy milyen gyorsan akarunk elmozdulni a minimum felé. Ha azonban túl nagy a szám, akkor túllőhetünk.

mindent összehozni-lineáris regresszió
gyorsan összefoglalva:
van egy hipotézisünk:

amire szükségünk van illeszkedjen a képzési adatainkhoz. Használhatunk olyan költségfüggvényt, mint az átlagos négyzet hiba:

amelyet gradiens ereszkedés segítségével minimalizálhatunk:

ami elvezet minket az első gépi tanulási algoritmusunkhoz, a lineáris regresszióhoz. A puzzle utolsó darabja, amelyet meg kell oldanunk egy működő lineáris regressziós modell elkészítéséhez, a költségfüggvény részleges levezetése:
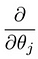
ami kiderül:
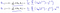
ami lineáris regressziót ad nekünk!
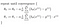
az elmélet az útból, megyek, hogy végre ezt a logikát python a következő bejegyzésben.
Szerkesztés május 4.: közzétettem egy nyomon követést, amely a Költségfüggvény működésére összpontosít, beleértve egy intuíciót, hogyan kell kiszámítani kézzel és két különböző Python implementációt. Meg tudom csinálni a gradiens leereszkedést, majd hamarosan összehozom őket lineáris regresszióhoz.