használatával magyarázott orientált gradiensek hisztogramja Ismerje meg az OpenCV-t

ebben a bejegyzésben megismerjük az Oriented Gradients (HOG) funkcióleíró Hisztogramjának részleteit. Megtanuljuk, mi van a motorháztető alatt, és hogyan számítja ki ezt a leírót az OpenCV, a MATLAB és más csomagok.

ez a bejegyzés egy Képfelismeréssel és Objektumfelismeréssel foglalkozó sorozat része.

a sorozat oktatóanyagainak teljes listája az alábbiakban található:

1. képfelismerés hagyományos számítógépes látási technikákkal : 1. rész
2. orientált színátmenetek Hisztogramja : 2. rész
3. példa kód a képfelismeréshez : 3. rész
4. jobb szemérzékelő képzése: 4a. rész
5. Objektumérzékelés hagyományos számítógépes Látástechnikákkal : 4b. rész
6. saját OpenCV objektumdetektor kiképzése és tesztelése : 5. rész
7. képfelismerés mély tanulás segítségével : 6. rész
   • Bevezetés a neurális hálózatokba
   • a Feedforward neurális hálózatok megértése
   • képfelismerés konvolúciós neurális hálózatok segítségével
8. Objektumérzékelés mély tanulással: rész 7

sok minden bonyolultnak és titokzatosnak tűnik. De amint időt szánsz arra, hogy lebontsd őket, a rejtélyt felváltja a mesterség, és ez az, amit keresünk. Ha kezdő vagy, és nehéznek és titokzatosnak találod a számítógépes látást, emlékezz a következő

k : hogyan eszel egy elefántot ?
A : Egyszerre csak egy falatot!

mi az a Funkcióleíró?

a funkcióleíró egy kép vagy képjavítás ábrázolása, amely egyszerűsíti a képet hasznos információk kinyerésével és idegen információk eldobásával.

jellemzően egy funkcióleíró átalakít egy képet méret szélesség x magasság x 3 (csatornák) egy jellemző vektor / tömb hosszúságú N. A HOG funkcióleíró esetében a bemeneti kép mérete 64 x 128 x 3, a kimeneti funkcióvektor pedig 3780 hosszúságú.

ne feledje, hogy a HOG leíró más méretekre is kiszámítható, de ebben a bejegyzésben ragaszkodom az eredeti cikkben bemutatott számokhoz, így egy konkrét példával könnyen megértheti a koncepciót.

mindez jól hangzik, de mi a “hasznos” és mi az “idegen” ? A “hasznos” meghatározásához tudnunk kell, hogy mi a “hasznos”? Nyilvánvaló, hogy a funkcióvektor nem hasznos a kép megtekintéséhez. De nagyon hasznos olyan feladatokhoz, mint a képfelismerés és az objektumfelismerés. Az ezen algoritmusok által előállított funkcióvektor, amikor olyan képosztályozási algoritmusokba kerül, mint a Support Vector Machine (SVM), jó eredményeket hoz.

de milyen” funkciók ” hasznosak az osztályozási feladatokhoz ? Beszéljük meg ezt a pontot egy példa segítségével. Tegyük fel, hogy szeretnénk építeni egy tárgy detektor, amely érzékeli gombok ingek és kabátok.

a gomb kör alakú ( a képen elliptikusnak tűnhet), és általában néhány lyuk van a varráshoz. Futtathat egy éldetektort egy gomb képén, és egyszerűen megmondhatja, hogy ez egy gomb, egyszerűen csak az élképre nézve. Ebben az esetben az élinformáció “hasznos”, a színinformáció pedig nem. Ezenkívül a jellemzőknek diszkriminatív erővel is rendelkezniük kell. Például a képből kinyert jó tulajdonságoknak meg kell tudniuk különböztetni a gombokat és más kör alakú tárgyakat, például érméket és autógumikat.

a HOG jellemző leíróban a színátmenetek ( orientált színátmenetek ) irányainak eloszlását ( hisztogramjait ) használják jellemzőként. A kép színátmenetei ( x és y származékok ) azért hasznosak, mert a színátmenetek nagysága nagy az élek és a sarkok körül ( a hirtelen intenzitásváltozások régiói), és tudjuk, hogy az élek és a sarkok sokkal több információt tartalmaznak az objektum alakjáról, mint a lapos régiók.

hogyan lehet kiszámítani az orientált gradiensek Hisztogramját ?

ebben a részben a HOG funkcióleíró kiszámításának részleteivel foglalkozunk. Az egyes lépések szemléltetéséhez egy kép javítását fogjuk használni.

1. lépés : Előfeldolgozás

mint korábban említettük, a gyalogos észleléshez használt HOG funkcióleírót egy kép 64 628-as javításán számítják ki. Természetesen a kép bármilyen méretű lehet. Általában a több skálán lévő javításokat sok képhelyen elemzik. Az egyetlen korlátozás az, hogy az elemzett javítások rögzített képaránnyal rendelkeznek. Esetünkben a javításoknak 1:2 képarányúnak kell lenniük. Ezek lehetnek például 100 200, 128 256, vagy 1000 2000, de nem 101 205.

ennek szemléltetésére egy 720 675-ös méretű nagy képet mutattam. Kiválasztottunk egy patch méretű 100 db 200 kiszámításához a HOG jellemző leíró. Ezt a javítást kivágják egy képből, és átméretezik 64 628-ra. Most készen állunk arra, hogy kiszámítsuk a disznó leíróját ehhez a képjavításhoz.

Dalal és Triggs tanulmánya a gamma-korrekciót is előfeldolgozási lépésként említi, de a teljesítménynövekedés csekély, ezért kihagyjuk a lépést.

2. lépés: a gradiens képek kiszámítása

a HOG leíró kiszámításához először ki kell számolnunk a vízszintes és függőleges gradienseket; végül is szeretnénk kiszámítani a gradiensek hisztogramját. Ez könnyen elérhető a kép szűrésével a következő magokkal.

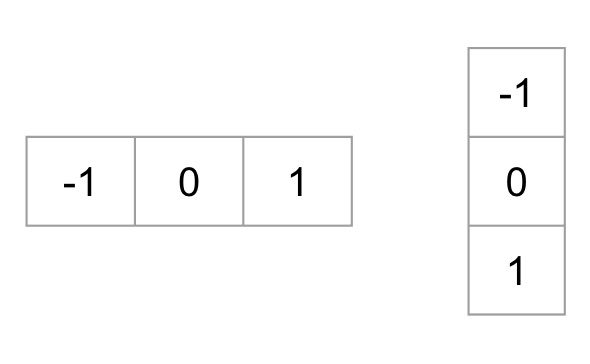
azt is elérni ugyanazt az eredményt, segítségével Sobel operátor OpenCV kernel mérete 1.

// C++ gradient calculation.// Read imageMat img = imread("bolt.png");img.convertTo(img, CV_32F, 1/255.0);// Calculate gradients gx, gyMat gx, gy;Sobel(img, gx, CV_32F, 1, 0, 1);Sobel(img, gy, CV_32F, 0, 1, 1);

# Python gradient calculation # Read imageim = cv2.imread('bolt.png')im = np.float32(im) / 255.0# Calculate gradientgx = cv2.Sobel(img, cv2.CV_32F, 1, 0, ksize=1)gy = cv2.Sobel(img, cv2.CV_32F, 0, 1, ksize=1)

ezután a gradiens nagyságát és irányát a következő képlet segítségével találhatjuk meg

ha OpenCV-t használ, akkor a számítást a függvény segítségével lehet elvégezni cartToPolar az alábbiak szerint.

// C++ Calculate gradient magnitude and direction (in degrees)Mat mag, angle;cartToPolar(gx, gy, mag, angle, 1);

ugyanaz a kód a Pythonban így néz ki.

# Python Calculate gradient magnitude and direction ( in degrees )mag, angle = cv2.cartToPolar(gx, gy, angleInDegrees=True)

az alábbi ábra a színátmeneteket mutatja.

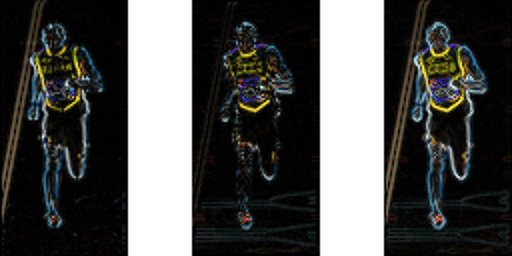
figyeljük meg, hogy az x-gradiens függőleges vonalakon, az y-gradiens pedig vízszintes vonalakon világít. A gradiens tüzek nagysága, ahol valaha éles intenzitásváltozás tapasztalható. Egyikük sem lő, ha a régió sima. Szándékosan kihagytam a gradiens irányát mutató képet, mert a képként megjelenített irány nem sokat közvetít.

a gradiens kép eltávolított sok nem lényeges információt ( pl. állandó színes háttér ), de Kiemelt körvonalakat. Más szavakkal, megnézheti a gradiens képet, és még mindig könnyen azt mondhatja, hogy van egy személy a képen.

minden képpontnál a gradiensnek van egy nagysága és egy iránya. Színes képek esetén a három csatorna színátmeneteit értékeljük (amint az a fenti ábrán látható ). A képpont gradiensének nagysága a három csatorna gradienseinek nagyságának maximuma, a szög pedig a maximális gradiensnek megfelelő szög.

3. lépés: a gradiensek Hisztogramjának kiszámítása 8 db 8 cellában

ebben a lépésben a kép 8 db 8 db 8 db cellára van felosztva, és mindegyik 8 db 8 db cellára gradiensek hisztogramját számítjuk ki.

egy pillanat alatt megismerjük a hisztogramokat, de mielőtt odamennénk, először értsük meg, miért osztottuk a képet 8 db 8 cellára. A funkcióleíró használatának egyik fontos oka a kép javításának leírására az, hogy kompakt ábrázolást biztosít. Egy 8 db 8 képjavítás 8x8x3 = 192 képpont értéket tartalmaz. Ennek a javításnak a gradiense 2 értéket tartalmaz ( nagyság és irány ) pixelenként, ami 8x8x2 = 128 számot ad össze.

e szakasz végére látni fogjuk, hogy ezek a 128 számok egy 9 bin hisztogram segítségével vannak ábrázolva, amely 9 szám tömbjeként tárolható. Nem csak az ábrázolás kompaktabb, a hisztogram kiszámítása egy javítás felett robusztusabbá teszi ezt az ábrázolást a zaj szempontjából. Az egyes graidenseknek zajuk lehet, de a hisztogram vége 8 6.számú javítás miatt az ábrázolás sokkal kevésbé érzékeny a zajra.

de miért 8 6db folt? Miért nem 32 KB 32 ? Ez egy tervezési választás, amelyet a keresett funkciók skálája tájékoztat. A disznót kezdetben gyalogos észlelésre használták. 8 (6) 6 (128) – ra méretezett gyalogosfotó 8 (8) cellája elég nagy ahhoz, hogy érdekes vonásokat ( pl. az arcot, a fej tetejét stb.) rögzítsen. ).

a hisztogram lényegében egy vektor ( vagy tömb ) 9 tartályból ( számokból), amelyek megfelelnek a szögeknek 0, 20, 40, 60 … 160.

vessünk egy pillantást a képen látható 8 6.számú javításra, és nézzük meg, hogyan néznek ki a színátmenetek.

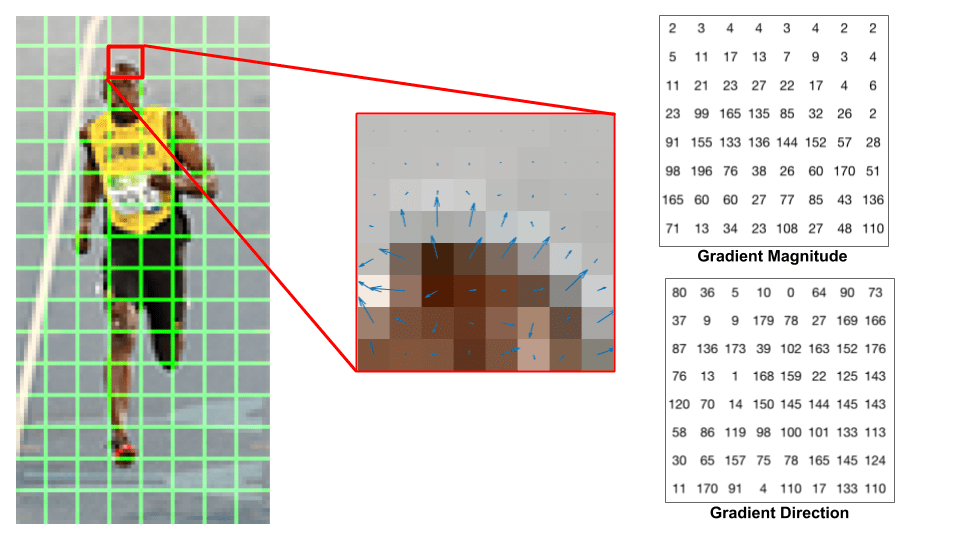
ha kezdő vagy a számítógépes látásban, a központban lévő kép nagyon informatív. Megmutatja a kép foltját, amely a gradienst mutató nyilakkal van átfedve — a nyíl a gradiens irányát, hossza pedig a nagyságot mutatja. Figyelje meg, hogy a nyilak iránya hogyan mutat az intenzitás változásának irányára, a nagyság pedig megmutatja, hogy mekkora a különbség.

a jobb oldalon látjuk a nyers számokat, amelyek a gradienseket képviselik a 8-8.számú cellában, egy kisebb különbséggel — a szögek 0 és 180 fok között vannak a 0-360 fok helyett. Ezeket “aláíratlan” színátmeneteknek nevezzük, mert a gradienst és annak negatívját ugyanazok a számok képviselik. Más szavakkal, a gradiens nyíl és a vele szemben lévő 180 fok ugyanaz. De miért nem használja a 0-360 fokot ?

empirikusan kimutatták, hogy az aláíratlan színátmenetek jobban működnek, mint az aláírt színátmenetek a gyalogosok észleléséhez. A HOG egyes implementációi lehetővé teszik annak meghatározását, hogy aláírt színátmeneteket szeretne-e használni.

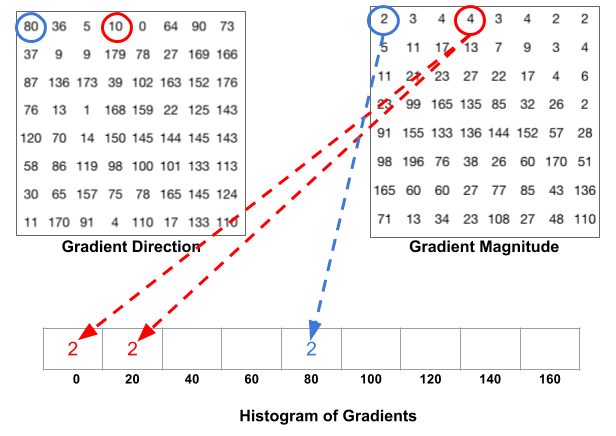
a következő lépés a gradiensek hisztogramjának létrehozása ezekben a 8 6. számú cellában. A hisztogram 9 tartályt tartalmaz, amelyek megfelelnek a 0, 20, 40 … 160 szögnek. Az alábbi ábra szemlélteti a folyamatot. Nézzük nagysága és iránya a gradiens az azonos 8 .. 8 folt, mint az előző ábrán.

a bin az irány alapján kerül kiválasztásra, a szavazás ( a bin-be kerülő érték ) pedig a nagyság alapján kerül kiválasztásra. Először összpontosítsunk a kékkel körülvett pixelre. Szöge (iránya ) 80 fok, nagysága pedig 2. Tehát 2-t ad az 5. kukához. A pirossal körülvett képpont gradiensének szöge 10 fok, nagysága pedig 4. Mivel a 10 fok félúton van 0 és 20 között, a pixel szavazata egyenletesen oszlik el a két kukába.

van még egy részlet, amellyel tisztában kell lennie. Ha a szög nagyobb, mint 160 fok, akkor 160 és 180 között van, és tudjuk, hogy a szög 0 és 180 egyenértékűvé válik. Tehát az alábbi példában a 165 fokos szögű pixel arányosan járul hozzá a 0 fokos tárolóhoz és a 160 fokos tárolóhoz.

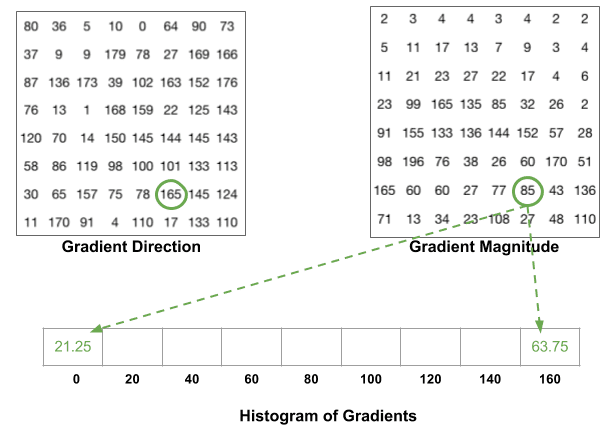
a hozzájárulások az összes pixel a 8-tól 8 cellák összeadjuk, hogy megteremtse a 9-bin hisztogram. A fenti javításhoz így néz ki

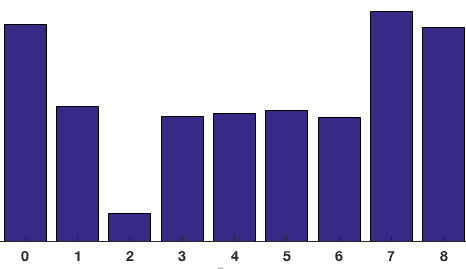
ábrázolásunkban az y tengely 0 fok. Láthatjuk, hogy a hisztogramnak nagy súlya van 0 és 180 fok közelében, ami csak egy másik módja annak, hogy a tapaszban a gradiensek felfelé vagy lefelé mutatnak.

4. lépés : 16 db 16 blokk normalizálás

az előző lépésben hisztogramot hoztunk létre a kép gradiense alapján. A kép színátmenetei érzékenyek az Általános megvilágításra. Ha sötétebbé teszi a képet úgy, hogy az összes pixelértéket elosztja 2-vel, akkor a gradiens nagysága felére változik, ezért a hisztogram értékei felére változnak.

ideális esetben azt akarjuk, hogy a leírónk független legyen a világítási variációktól. Más szavakkal, szeretnénk “normalizálni” a hisztogramot, hogy a világítási variációk ne befolyásolják őket.

mielőtt elmagyaráznám, hogyan normalizálódik a hisztogram, nézzük meg, hogyan normalizálódik a 3 hosszúságú vektor.

tegyük fel, hogy van egy RGB színvektorunk . Ennek a vektornak a hossza $\sqrt{128^2 + 64^2 + 32^2} = 146.64$. Ezt a vektor L2 normájának is nevezik. Ennek a vektornak az egyes elemeit elosztva 146,64-gyel normalizált vektort kapunk .

most tekintsünk egy másik vektort, amelyben az elemek kétszerese az első 2 x = vektor értékének . Ön is kidolgozhatja, hogy lássa, hogy a normalizálás azt eredményezi, ami megegyezik az eredeti RGB vektor normalizált változatával. Láthatja, hogy a vektor normalizálása eltávolítja a skálát.

most, hogy tudjuk, hogyan kell normalizálni egy vektort, kísértésbe eshet, hogy azt gondolja, hogy a HOG kiszámításakor egyszerűen normalizálhatja a 9 .. 1.számú hisztogramot, ugyanúgy, mint a fenti 3 .. 6. számú vektort. Ez nem egy rossz ötlet,de egy jobb ötlet, hogy normalizálja több mint egy nagyobb méretű blokk 16 6db 16.

egy 16 6-os blokknak 4 hisztogramja van, amelyek összefűzhetők egy 36 x 1-es elemvektorral, és ugyanúgy normalizálhatók, mint egy 3 6-os 1-es vektor. Ezután az ablakot 8 képponttal mozgatjuk (lásd az animációt), és egy normalizált 36 6db vektort számítunk ki ezen az ablakon, és a folyamat megismétlődik.

5.lépés : Számítsa ki a HOG funkcióvektort

a teljes képjavítás végső funkcióvektorának kiszámításához a 36 db 1 vektor egy óriási vektorba van összefűzve. Mekkora ennek a vektornak a mérete ? Számítsuk ki

1. hány pozíciónk van a 16 db 16 blokkból ? 7 vízszintes és 15 függőleges pozíció van, így összesen 7 x 15 = 105 pozíció.
2. minden 16 db 16 blokk egy 36 db 1 vektorral van ábrázolva. Tehát, ha összefűzzük őket egy gaint vektorba, akkor 36 605 = 3780 dimenziós vektort kapunk.

orientált színátmenetek Hisztogramjának megjelenítése

a képjavítás DISZNÓLEÍRÓJÁT általában a 9 6. számú normalizált hisztogram ábrázolásával jelenítik meg a 8 8.számú cellában. Lásd a képet az oldalon. Észre fogja venni, hogy a hisztogram domináns iránya rögzíti a személy alakját, különösen a törzs és a lábak körül.

sajnos nincs egyszerű módszer a HOG leíró megjelenítésére az OpenCV-ben.

Feliratkozás & Letöltési Kód