az e elektromos mező mindig kifejezhető egy skaláris potenciálfüggvény gradienseként
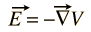
a B mágneses mezőnek nincs általános skaláris potenciálja, de kifejezhető egy vektorfüggvény görbületeként
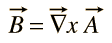
ennek az a függvénynek a neve “vektorpotenciál”, de nem kapcsolódik közvetlenül a munkához, ahogy a skaláris potenciál.
a vektorpotenciál meghatározása szerint összhangban van az Amper törvényével, és kifejezhető i árammal vagy j áramsűrűséggel (a mágneses mező forrásaival). Különböző szövegekben ez a meghatározás a következő formákat ölti
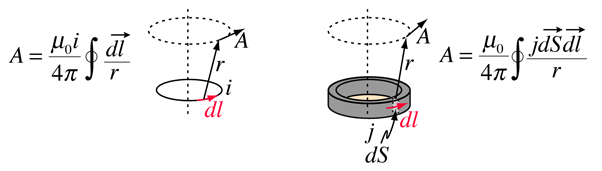
a vektorpotenciál egyik oka, hogy könnyebb lehet kiszámítani a vektorpotenciált, mint a mágneses mezőt közvetlenül egy adott forrásáram geometriájából kiszámítani. Leggyakoribb alkalmazása az antennaelmélet és az elektromágneses hullámok leírása.
mivel a B mágneses mező az a görbületeként van meghatározva, és a vektorazonosság szerint a gradiens görbülete azonos nulla, akkor bármely tetszőleges függvény, amely egy skaláris függvény gradienseként fejezhető ki, hozzáadható az A-hoz anélkül, hogy megváltoztatná az abból kapott B értékét. Vagyis a ‘ szabadon helyettesíthető a hol
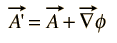
az ilyen transzformációkat gauge transzformációknak nevezzük, és számos olyan “mérőeszköz” létezik, amelyeket az elektromágneses elmélet bizonyos típusú számításainak előnyére használtak.