az optimális megoldás megtalálása bizonyos optimalizálási problémákra hihetetlenül nehéz feladat lehet, gyakran gyakorlatilag lehetetlen. Ez azért van, mert amikor egy probléma elég nagy lesz, hatalmas számú lehetséges megoldást kell keresnünk az optimális megtalálásához. Még a modern számítási teljesítmény mellett is gyakran túl sok lehetséges megoldást kell figyelembe venni. Ebben az esetben, mivel reálisan nem számíthatunk arra, hogy ésszerű időn belül megtaláljuk az optimálisat, meg kell elégednünk valamivel, ami elég közel van.
egy példa optimalizálási probléma, amely általában számos lehetséges megoldás lenne az utazó eladó probléma. Annak érdekében, hogy megoldást találjunk egy olyan problémára, mint az utazó eladó probléma, olyan algoritmust kell használnunk, amely képes ésszerű időn belül elég jó megoldást találni. Egy korábbi oktatóanyagban megvizsgáltuk, hogyan tudnánk ezt genetikai algoritmusokkal megtenni, és bár a genetikai algoritmusok az egyik módja annak, hogy megtaláljuk az ‘elég jó’ megoldást az utazó eladó problémájára, vannak más egyszerűbb algoritmusok is, amelyeket megvalósíthatunk, amelyek szintén közel optimális megoldást találnak nekünk. Ebben az oktatóanyagban az algoritmus, amelyet használni fogunk, ‘szimulált lágyítás’.
ha nem ismeri az utazó eladó problémáját, érdemes lehet megnézni az előző bemutatómat, mielőtt folytatnám.
mi a szimulált lágyítás?
először nézzük meg, hogyan működik a szimulált lágyítás, és miért jó megoldást találni különösen az utazó eladó problémájára. A szimulált hőkezelési algoritmust eredetileg a fémmegmunkálás során végzett hőkezelés ihlette. A hőkezelés magában foglalja az anyag fűtését és hűtését, hogy megváltoztassa fizikai tulajdonságait a belső szerkezetének változásai miatt. Ahogy a fém lehűl, új szerkezete rögzül, következésképpen a fém megtartja újonnan kapott tulajdonságait. A szimulált hőkezelés során hőmérsékleti változót tartunk a fűtési folyamat szimulálására. Kezdetben magasra állítottuk, majd hagyjuk lassan lehűlni az algoritmus futása közben. Míg ez a hőmérsékleti változó magas, az algoritmus nagyobb gyakorisággal képes elfogadni a jelenlegi megoldásunknál rosszabb megoldásokat. Ez lehetővé teszi az algoritmus számára, hogy kiugorjon minden olyan helyi optimumból, amelyben a végrehajtás elején találja magát. Mivel a hőmérséklet csökken, így van esély a rosszabb megoldások elfogadására, ezért lehetővé teszi az algoritmus számára, hogy fokozatosan összpontosítson a keresési tér egy olyan területére, amelyben remélhetőleg az optimálishoz közeli megoldás található. Ez a fokozatos ‘hűtési’ folyamat teszi a szimulált lágyítási algoritmust rendkívül hatékonynak az optimális megoldáshoz közeli megoldás megtalálásában, amikor olyan nagy problémákkal foglalkozik, amelyek számos helyi optimumot tartalmaznak. A természet az utazó eladó probléma teszi, hogy egy tökéletes példa.
a szimulált lágyítás előnyei
lehet, hogy kíváncsi, hogy van-e valódi előnye a szimulált lágyítás megvalósításának valami olyan felett, mint egy egyszerű hegymászó. Bár a hegymászók meglepően hatékonyak lehetnek a jó megoldás megtalálásában, hajlamosak elakadni a helyi optimumokban is. Amint azt korábban megállapítottuk, a szimulált lágyítási algoritmus kiválóan képes elkerülni ezt a problémát, és átlagosan sokkal jobb a hozzávetőleges globális optimum megtalálásában.
annak érdekében, hogy jobban megértsük, vessünk egy pillantást arra, hogy egy alapvető hegymászó algoritmus miért hajlamos arra, hogy elkapjon a helyi optimumokban.
a hegymászó algoritmus egyszerűen elfogadja a szomszéd megoldásokat, amelyek jobbak, mint a jelenlegi megoldás. Amikor a hegymászó nem talál jobb szomszédokat, megáll.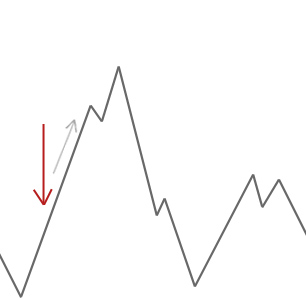
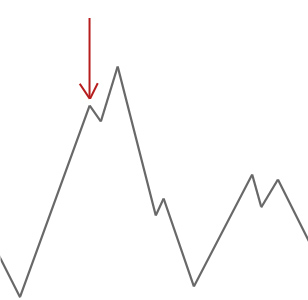
a fenti példában a hegymászót a piros nyílnál kezdjük, és felfelé halad a dombon, amíg el nem éri azt a pontot, ahol nem tud magasabbra mászni anélkül, hogy először leereszkedne. Ebben a példában világosan láthatjuk, hogy beragadt egy helyi optimumba. Ha ez egy valós probléma lenne, nem tudnánk, hogyan néz ki a keresési tér, így sajnos nem tudnánk megmondani, hogy ez a megoldás közel áll-e a globális optimumhoz.
a szimulált lágyítás ettől kissé eltérően működik, és alkalmanként rosszabb megoldásokat is Elfogad. A szimulált lágyítás ezen jellemzője segít abban, hogy kiugorjon minden olyan helyi optimumból, amelybe egyébként beragadt.
elfogadási funkció
vessünk egy pillantást arra, hogy az algoritmus hogyan dönti el, mely megoldásokat fogadja el, hogy jobban megértsük, hogyan képes elkerülni ezeket a helyi optimumokat.
először ellenőrizzük, hogy a szomszéd megoldás jobb-e, mint a jelenlegi megoldás. Ha igen, akkor feltétel nélkül elfogadjuk. Ha azonban a szomszéd megoldás nem jobb, akkor néhány tényezőt figyelembe kell vennünk. Először is, mennyivel rosszabb a szomszéd megoldás; másodszor pedig, hogy milyen magas a rendszerünk jelenlegi ‘hőmérséklete’. Magas hőmérsékleten a rendszer nagyobb valószínűséggel fogadja el a rosszabb megoldásokat.
a matematika erre nagyon egyszerű:
alapvetően minél kisebb az energiaváltozás (a megoldás minősége), és minél magasabb a hőmérséklet, annál valószínűbb, hogy az algoritmus elfogadja a megoldást.
algoritmus áttekintés
tehát hogyan néz ki az algoritmus? Nos, a legalapvetőbb megvalósításában elég egyszerű.
- először meg kell állítanunk a kezdeti hőmérsékletet, és létre kell hoznunk egy véletlenszerű kezdeti megoldást.
- ezután elkezdjük a hurkolást, amíg a stop feltételünk nem teljesül. Általában vagy a rendszer kellően lehűlt, vagy elég jó megoldást találtak.
- innen választunk ki egy szomszédot egy kis változtatással a jelenlegi megoldásunkon.
- ezután eldöntjük, hogy áttérünk-e a szomszédos megoldásra.
- végül csökkentjük a hőmérsékletet és folytatjuk a hurkolást
hőmérséklet inicializálás
a jobb optimalizálás érdekében a hőmérsékletváltozó inicializálásakor olyan hőmérsékletet kell választanunk, amely kezdetben gyakorlatilag bármilyen mozgást lehetővé tesz az aktuális megoldással szemben. Ez lehetővé teszi az algoritmus számára, hogy jobban felfedezze a teljes keresési helyet, mielőtt lehűlne és egy fókuszáltabb régióban telepedne le.
példa kód
most használjuk azt, amit tudunk, hogy létrehozzunk egy alapvető szimulált lágyítási algoritmust, majd alkalmazzuk az alábbi utazó eladó problémára. Ebben az oktatóanyagban a Java-t fogjuk használni, de a logikának remélhetőleg elég egyszerűnek kell lennie ahhoz, hogy bármely választott nyelvre másolhassa.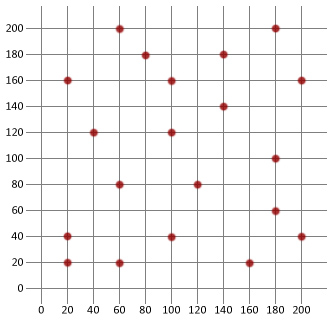
először létre kell hoznunk egy városi osztályt, amely felhasználható utazó értékesítőnk különböző célállomásainak modellezésére.
város.java
* város.java
* modellek a város
* /
csomag sa;
nyilvános osztály város {
int x;
Int y;
/ / véletlenszerűen elhelyezett várost épít
public City () {
ezt.x = (int) (matematika.véletlen ()*200);
ezt.y = (int) (matematika.véletlen()*200);
}
// épít egy várost a kiválasztott x, y helyen
nyilvános város (int x, Int y){
ezt.x = x;
ezt.y = y;
}
// Gets város x koordináta
public int getX () {
vissza ezt.x;
}
// Gets város y koordináta
public Int getY () {
vissza ezt.y;
}
// megkapja a távolságot az adott város
public double distanceTo (város város){
int xDistance = Math.abs (getX () – város.getX());
int yDistance = matematika.abs (getY () – város.getY ());
dupla távolság = matematika.sqrt ((xDistance*xDistance) + (yDistance*yDistance) );
visszatérési távolság;
}
@felülírás
nyilvános karakterlánc toString () {
return getX ()+”, ” + getY();
}
}
ezután hozzunk létre egy osztályt, amely nyomon tudja követni a városokat.
TourManager.java
* TourManager.java
*tartja a városok egy túra
* /
csomag sa;
import java.util.ArrayList;
nyilvános osztály TourManager {
/ / tartja városainkat
privát statikus ArrayList destinationCities = új ArrayList<város>();
// célváros hozzáadása
nyilvános statikus void addCity (város város) {
destinationCities.add (város);
}
// kap egy város
nyilvános statikus város getCity (int index){
return (város)destinationCities.get (index);
}
// Szerezd meg a célvárosok számát
nyilvános statikus int numberOfCities () {
return destinationCities.méret();
}
}
most, hogy hozzon létre az osztály, amely modellezni egy utazó eladó túra.
túra.java
* túra.java
*jelölt túrát tárol az összes városban
* /
sa csomag;
java importálása.util.ArrayList;
java importálása.util.Gyűjtemények;
nyilvános osztálytúra{
/ / tartja a városok túráját
privát ArrayList tour = új ArrayList<város>();
// gyorsítótár
privát int távolság = 0;
// üres túrát készít
nyilvános túra(){
for (int i = 0; i < TourManager.numberOfCities (); i++) {
túra.add (null);
}
}
// épít egy túra egy másik túra
public Tour (ArrayList tour){
ezt.túra = (ArrayList) túra.klón();
}
// Returns tour information
nyilvános ArrayList getTour () {
return tour;
}
// létrehoz egy véletlenszerű egyéni
nyilvános void generateIndividual () {
// hurok az összes célvárosok és add hozzá a túra
(int cityIndex = 0; cityIndex < TourManager.numberOfCities (); cityIndex++) {
setCity (cityIndex, TourManager.getcity (cityIndex));
}
// véletlenszerűen rendezze át a túrát
gyűjtemények.shuffle (túra);
}
/ / kap egy város a túra
public City getCity (int tourPosition) {
return (City)túra.get (tourPosition);
}
// Beállítja a város egy bizonyos helyzetben egy túra
public void setCity (int tourPosition, City city) {
túra.set (tourPosition, city);
/ / ha a túrákat megváltoztattuk, vissza kell állítanunk a fitnesz és a távolság
távolságot = 0;
}
// megkapja a túra teljes távolságát
nyilvános int getDistance () {
if (távolság == 0) {
int tourDistance = 0;
/ / hurok a túra városain keresztül
for (int cityIndex=0; cityIndex < tourSize(); cityIndex++) {
// Get city utazunk
City fromCity = getCity(cityIndex);
// város utazunk
City destinationCity;
// ellenőrizze nem vagyunk a túra utolsó város, ha meg vagyunk állítva a
// túra végső cél város a kiindulási város
if(cityindex+1 < toursize()){
destinationcity = getcity(cityindex+1);
}
else{
destinationCity = getCity(0);
}
// Szerezd meg a két város közötti távolságot
tourDistance += fromCity.distanceTo (destinationCity);
}
distance = tourDistance;
}
visszatérési távolság;
}
// Get városok száma a túra
public int tourSize () {
vissza túra.méret();
}
@felülírás
nyilvános karakterlánc toString () {
karakterlánc geneString =”/”;
for (int i = 0; i < tourSize (); i++) {
geneString += getCity (i)+”|”;
}
vissza geneString;
}
}
végül hozzuk létre szimulált lágyítási algoritmusunkat.
SimulatedAnnealing.java
nyilvános osztály SimulatedAnnealing {
/ / Számítsa ki az elfogadási valószínűséget
nyilvános statikus kettős elfogadásprobability (int energia, int newenergia, dupla hőmérséklet) {
/ / ha az új megoldás jobb, fogadja el
ha (newEnergy < energia) {
visszatérés 1.0;
}
// ha az új megoldás rosszabb, számítsa ki az elfogadási valószínűséget
visszatérési matematika.exp ((energia-newEnergy) / hőmérséklet);
}
nyilvános statikus void main(String args) {
// városaink létrehozása és hozzáadása
város város = új város(60, 200);
TourManager.addCity (város);
City city2 = új város(180, 200);
TourManager.addCity (city2);
City city3 = új város(80, 180);
TourManager.addCity (city3);
City city4 = új város(140, 180);
TourManager.addCity (city4);
City city5 = új város(20, 160);
TourManager.addCity (city5);
City city6 = új város(100, 160);
TourManager.addCity (city6);
City city7 = új város(200, 160);
TourManager.addCity (city7);
City city8 = új város(140, 140);
TourManager.addCity (city8);
City city9 = új város(40, 120);
TourManager.addCity (város9);
City city10 = új város(100, 120);
TourManager.addCity (city10);
City city11 = új város(180, 100);
TourManager.addCity (city11);
City city12 = új város(60, 80);
TourManager.addCity (city12);
City city13 = új város(120, 80);
TourManager.addCity (city13);
City city14 = új város(180, 60);
TourManager.addCity (city14);
City city15 = új város(20, 40);
TourManager.addCity (city15);
City city16 = új város(100, 40);
TourManager.addCity (city16);
City city17 = új város(200, 40);
TourManager.addCity (város17);
City city18 = új város (20, 20);
TourManager.addCity (city18);
City city19 = új város(60, 20);
TourManager.addCity (city19);
City city20 = új város(160, 20);
TourManager.addCity (city20);
// kezdeti hőmérséklet beállítása
dupla hőmérséklet = 10000;
// hűtési sebesség
dupla hűtési sebesség = 0,003;
// inicializálja az intial megoldást
Tour currentSolution = new Tour ();
currentSolution.generateIndividual ();
rendszer.kifelé.println (“kezdeti megoldás távolság:” + currentSolution.getDistance ());
// állítsa be a jelenlegi legjobb
Tour best = új túra (currentSolution.getTour ());
/ / hurok, amíg a rendszer lehűlt
while (temp > 1) {
// új szomszéd túra létrehozása
Tour newSolution = új túra (currentSolution.getTour ());
/ / kap egy véletlen pozíciók a túra
int tourPos1 = (int) (newSolution.tourSize () * matematika.véletlen ());
int tourPos2 = (int) (newSolution.tourSize () * matematika.random ());
/ / Szerezd meg a városokat a túra kiválasztott pozícióiban
City citySwap1 = newSolution.getCity (tourPos1);
City citySwap2 = newSolution.getCity (tourPos2);
// Swap őket
newSolution.setCity(tourPos2, citySwap1);
newSolution.setCity (tourPos1, citySwap2);
// a megoldások energiájának megszerzése
int currentEnergy = currentSolution.getDistance ();
int neighbourEnergy = newSolution.getDistance();
// döntse el, hogy elfogadjuk-e a szomszédot
if (acceptanceProbability(currentEnergy, neighbourEnergy, temp) > matematika.random ()) {
currentSolution = új túra (newSolution.getTour());
}
// Kövesse nyomon a legjobb megoldást
if (currentSolution.getDistance () < legjobb.getDistance ()) {
best = új túra (currentSolution.getTour());
}
// hűtőrendszer
temp * = 1-hűtési sebesség;
}
rendszer.kifelé.println (“végső megoldás távolsága:” + legjobb.getDistance ());
rendszer.kifelé.println (“túra:” + legjobb);
}
}
kimenet
végső megoldás távolság: 911
túra: |180, 200/200, 160/140, 140/180, 100/180, 60/200, 40/160, 20/120, 80/100, 40/60, 20/20, 20/20, 40/60, 80/100, 120/40, 120/20, 160/60, 200/80, 180/100, 160/140, 180|
következtetés
ebben a példában a kezdeti véletlenszerűen generált útvonalunk távolságának több mint felét tudtuk megtenni. Ez remélhetőleg megmutatja, mennyire hasznos ez a viszonylag egyszerű algoritmus, ha bizonyos típusú optimalizálási problémákra alkalmazzák.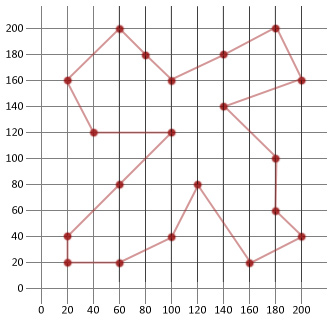
szerző
 Helló, Lee vagyok.
Helló, Lee vagyok.fejlesztő vagyok az Egyesült Királyságból, aki szereti a technológiát és az üzletet. Itt találsz cikkeket és oktatóanyagokat azokról a dolgokról, amelyek érdekelnek. Ha azt szeretnénk, hogy bérel engem, vagy többet rólam feje fölött a magamról oldal