特定の最適化問題の最適解を見つけることは、信じられないほど困難な作業であり、 これは、問題が十分に大きくなると、最適な解決策を見つけるために膨大な数の可能な解決策を検索する必要があるためです。 現代のコンピューティングパワーでさえ、考慮すべき解決策が多すぎることがよくあります。 この場合、合理的な時間内に最適なものを見つけることを現実的に期待することはできないため、十分に近いものを解決する必要があります。
最適化問題の例では、通常、多くの可能な解決策があります旅行セールスマン問題になります。 旅行セールスマンの問題などの問題に対する解決策を見つけるためには、合理的な時間内に十分な解決策を見つけることができるアルゴリズムを使 前のチュートリアルでは、我々は遺伝的アルゴリズムでこれを行うことができる方法を見て、遺伝的アルゴリズムは、我々は旅行セールスマンの問題に”十分に良い”解を見つけることができる一つの方法ですが、我々はまた、私たちに最適な解に近い見つけることができます他の簡単なアルゴリズムを実装することができますがあります。 このチュートリアルでは、使用するアルゴリズムは’simulated annealing’です。
あなたが旅行セールスマンの問題に精通していない場合は、続行する前に私の前のチュートリアルを見てみる価値があるかもしれません。
シミュレーテッドアニーリングとは何ですか?
まず、シミュレーテッドアニーリングがどのように機能するのか、そしてなぜそれが特に旅行セールスマン問題の解決策を見つけるのが得意なのかを見てみましょう。 シミュレーテッドアニーリングアルゴリズムは,もともと金属加工におけるアニーリングのプロセスから着想を得たものである。 アニーリングは、材料の内部構造の変化によりその物理的性質を変化させるために材料を加熱および冷却することを含む。 金属が冷却すると、その新しい構造が固定され、その結果、金属は新たに得られた特性を保持する。 シミュレーテッドアニーリングでは,この加熱プロセスをシミュレートするために温度変数を維持した。 私たちは最初にそれを高く設定し、アルゴリズムの実行中にゆっくりと”冷却”できるようにします。 この温度変数が高い間、アルゴリズムは私達の現在の解決より悪い解決を受け入れるために、より多くの頻度と、許可される。 これにより、アルゴリズムは、実行の早い段階で自分自身を見つけたローカルの最適化から飛び降りることができます。 温度が低下するにつれて、より悪い解を受け入れる可能性があるため、アルゴリズムは徐々に最適解に近い解を見つけることができる探索空間の領域に焦点を当てることができます。 この段階的な”冷却”プロセスは、シミュレーテッドアニーリングアルゴリズムを、多数の局所最適値を含む大きな問題に対処するときに最適解に近い解を見つけるのに非常に効果的にするものです。 旅行のセールスマン問題の性質はそれに完全な例をする。
シミュレーテッドアニーリングの利点
単純なヒルクライマーのようなものよりもシミュレーテッドアニーリングを実装することに本当の利点があるかどうか疑問に思うかもしれません。 丘の登山者がよい解決を見つけることで意外にも有効である場合もあるがまたローカル最適で動けなくなる傾向がある。 先に決定したように,シミュレーテッドアニーリングアルゴリズムはこの問題を回避するのに優れており,近似的な大域的最適値を見つけるのに平均してはるかに優れている。
よりよく理解するために、基本的な山登りアルゴリズムがなぜ局所的な最適化に巻き込まれやすいのかをすばやく見てみましょう。
ヒルクライマーアルゴリズムは、現在の解よりも優れた近隣解を単に受け入れる。 ヒルクライマーは、任意のより良い隣人を見つけることができないとき、それは停止します。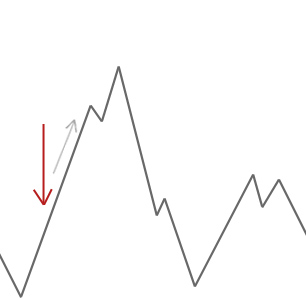
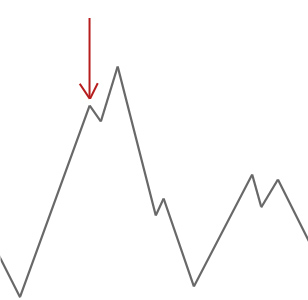
上の例では、私たちは赤い矢印で私たちのヒルクライマーをオフに開始し、それはそれが最初に降順せずに任意の高い登ることができないポイントに達 この例では、それが局所的な最適値で立ち往生していることがはっきりとわかります。 これが現実世界の問題であれば、検索空間がどのように見えるかわからないので、残念ながら、この解決策がグローバルな最適値に近いかどうかを判断
シミュレートされたアニーリングは、これとはわずかに異なり、時には悪い解を受け入れます。 シミュレートされたアニーリングのこの特性は、それ以外の場合に立ち往生している可能性のあるローカル最適値から飛び出すのに役立ちます。
Acceptance Function
アルゴリズムがどの解を受け入れるかを決定する方法を見て、これらのローカル最適化を回避する方法をよりよく理解できるようにしましょう。
まず、隣の解が現在の解よりも優れているかどうかを確認します。 それがあれば、私達はそれを無条件に受け入れます。 しかし、隣人の解決策が良くない場合は、いくつかの要因を考慮する必要があります。 第一に、隣人の解決策がどれくらい悪化しているか、そして第二に、私たちのシステムの現在の”温度”がどれくらい高いかです。 高温では、システムはより悪い解決策を受け入れる可能性が高くなります。
このための数学は非常に簡単です:
基本的に、エネルギーの変化(解の品質)が小さく、温度が高いほど、アルゴリズムが解を受け入れる可能性が高く
アルゴリズムの概要
アルゴリズムはどのように見えますか? まあ、その最も基本的な実装では、それは非常に簡単です。
- まず、初期温度を設定し、ランダムな初期解を作成する必要があります。
- その後、停止条件が満たされるまでループを開始します。 通常、システムが十分に冷却されているか、十分な解決策が見つかっています。
- ここから、現在の解決策を少し変更して隣人を選択します。
- 次に、その隣の解に移動するかどうかを決定します。
- 最後に、温度を下げてループを続けます
温度初期化
最適化のために、温度変数を初期化するときに、現在の解に対する実質的に任意の移動を最初に可能にする温度を選択する必要があり これにより、アルゴリズムは、より集中した領域に冷却して沈降する前に、探索空間全体をよりよく探索することができます。
サンプルコード
ここで、知っていることを使用して基本的なシミュレートアニーリングアルゴリズムを作成し、それを以下のtraveling salesman問題に適用しましょう。 私たちは、このチュートリアルでは、Javaを使用するつもりだが、ロジックはうまくいけば、お好みの任意の言語にコピーするのに十分な単純なはずです。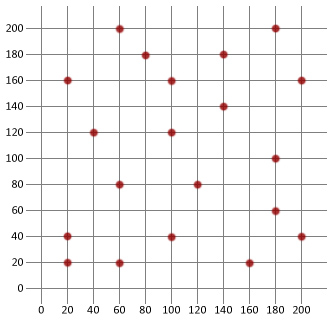
最初に、旅行セールスマンのさまざまな目的地をモデル化するために使用できるCityクラスを作成する必要があります。
java
*都市。java
*都市をモデル化
*/
パッケージsa;
public class City{
int x;
int y;
//ランダムに配置された都市を構築します
public City(){
this.x=(int)(Math.ランダム()*200);
これ。y=(int)(Math.ランダム()*200);
}
// 選択されたx,y位置に都市を構築します。
public City(int x,int y){
this.x=x;
これ。y=y;
}
// 都市のx座標を取得します
public int getX(){
これを返します。x;
}
// 都市のy座標を取得します
public int getY(){
これを返します。y;
}
// 指定された都市までの距離を取得します
public double distanceTo(City city){
int xDistance=Math.abs(getX()-都市。getX());
int yDistance=Math.abs(ゲティ()-都市。getY());
double distance=Math.sqrt((xDistance*xDistance)+(yDistance*yDistance));
return distance;
}
@Override
public String toString(){
return getX()+”,”+getY();
}
}
次に、都市を追跡できるクラスを作成しましょう。
java
*TourManager.java
*ツアーの都市を保持しています
*/
package sa;
javaをインポートします。ユーティルArrayList;
public class TourManager{
//都市を保持しています
private static ArrayList destinationCities=new ArrayList<City>();
// 宛先都市
public static void addCity(City city){
destinationCitiesを追加します。追加(都市);
}
// 都市を取得する
パブリック静的都市getCity(int index){
return(City)destinationCities。get(インデックス);
}
// 目的地の都市の数を取得
public static int numberOfCities(){
destinationCitiesを返します。サイズ();
}
}
今、旅行セールスマンのツアーをモデル化することができますクラスを作成します。
java
*ツアー。java
*すべての都市を通る候補ツアーを格納します
*/
package sa;
import java.ユーティルArrayList;
javaをインポートします。ユーティルCollections;
public class Tour{
//都市のツアーを開催
private ArrayList tour=new ArrayList<City>();
// Cache
private int distance=0;
//空白のツアーを構築します
public Tour(){
for(int i=0;i<TourManager.numberOfCities();i++){
ツアー。add(null);
}
}
//
ツアー=(ArrayList)ツアー。クローン();
}
// ツアー情報を返します
public ArrayList getTour(){
ツアーを返します;
}
// ランダムな個人を作成します
public void generateIndividual(){
//すべての目的地の都市をループし、それらをツアーに追加します
for(int cityIndex=0;cityIndex<TourManager。numberOfCities();cityIndex++){
setCity(cityIndex,TourManager.getCity(cityIndex));
}
// ツアー
shuffle(ツアー);
}
//ツアーから都市を取得します
public City getCity(int tourPosition){
return(City)ツアー。get(tourPosition);
}
// ツアー内の特定の位置に都市を設定します
public void setCity(int tourPosition,City city){
ツアー。set(tourPosition,city);
//ツアーが変更された場合、フィットネスと距離をリセットする必要があります
距離= 0;
}
// ツアーの合計距離を取得します。
public int getDistance(){
if(distance==0){
int tourDistance=0;
//ツアーの都市をループします。
for(int cityIndex=0; cityIndex<tourSize();cityIndex++){
//旅行している都市を取得
City fromCity=getCity(cityIndex);
//旅行している都市
City destinationCity;
//
//ツアーの最終目的地の都市を開始都市に設定している場合、ツアーの最後の都市ではないことを確認しますif(cityIndex+){
if(cityIndex+)){
//ツアーの最終目的地の都市を開始都市に設定している場合、
if(cityIndex+)){
//ツアーの最終目的地の都市を開始都市に設定している場合、
if(cityIndex+){
if(cityIndex+)1<toursize()){
destinationcity=getcity(cityindex+1);
}
else{
destinationCity=getCity(0);
}
// 二つの都市間の距離を取得
tourDistance+=fromCity.distanceTo(destinationCity);
}
distance=tourDistance;
}
戻り距離;
}
// ツアーの都市の数を取得する
public int tourSize(){
戻りツアー。サイズ();
}
@Override
public String toString(){
String geneString=”|”;
for(int i=0;i<tourSize();i++){
geneString+=getCity(i)+”|”;
}
geneStringを返す;
}
}
最後に、シミュレーテッドアニーリングアルゴリズムを作成しましょう。
java
public class SimulatedAnnealing{
//受け入れ確率を計算します
public static double acceptanceProbability(int energy,int newEnergy,double temperature){
//新しい解が優れている場合は、それを受け入れます
if(newEnergy<energy){
return1.0;
}
// 新しい解が悪い場合は、受け入れ確率
を計算してMathを返します。exp((energy-newEnergy)/temperature);
}
public static void main(String args){
//都市を作成して追加します
City city=new City(60,200);
TourManager。addCity(都市);
City city2=new City(180,200);
TourManager.addCity(city2);
City city3=new City(80,180);
TourManager.addCity(city3);
City4=new City(140,180);
TourManager.addCity(city4);
City city5=new City(20,160);
TourManager.addCity(city5);
City city6=new City(100,160);
TourManager.addCity(city6);
City7=new City(200,160);
TourManager.addCity(city7);
City city8=new City(140,140);
TourManager.addCity(city8);
City city9=new City(40,120);
TourManager.addCity(city9);
City city10=new City(100,120);
TourManager.addCity(city10);
City city11=new City(180,100);
TourManager.addCity(city11);
City city12=new City(60,80);
TourManager.addCity(city12);
City city13=new City(120,80);
TourManager.addCity(city13);
City14=new City(180,60);
TourManager.addCity(city14);
City15=new City(20,40);
TourManager.addCity(city15);
City city16=new City(100,40);
TourManager.addCity(city16);
City city17=new City(200,40);
TourManager.addCity(city17);
City city18=new City(20,20);
TourManager.addCity(city18);
City19=new City(60,20);
TourManager.addCity(city19);
City city20=new City(160,20);
TourManager.addCity(city20);
//初期温度を設定
double temp=10000;
//冷却速度
double coolingRate=0.003;
//初期解を初期化
Tour currentSolution=new Tour();
currentSolution。generateIndividual();
システム。出ろprintln(“初期解の距離:”+currentSolution.getDistance());
//現在のベストとして設定
ツアーベスト=新しいツアー(currentSolution.getTour());
//システムが冷却されるまでループします
while(temp> 1) {
// 新しい隣人ツアーを作成
ツアー newSolution=新しいツアー(currentSolution.getTour());
//ツアー内のランダムな位置を取得
int tourpos1=(int)(newSolution.tourSize()*数学.random());
int tourpos2=(int)(newSolution.tourSize()*数学.random());
//ツアー
City cityswap1=newSolutionで選択した位置にある都市を取得します。getCity(tourpos1);
City cityswap2=newSolution.getCity(tourpos2);
//
newSolutionをスワップします。setCity(tourpos2,cityswap1);
newSolution.setCity(tourpos1,cityswap2);
//ソリューションのエネルギーを取得
int currentEnergy=currentSolution.getDistance();
int=newSolution.getDistance();
//隣人を受け入れるかどうかを決定します
if(acceptanceProbability(currentEnergy,neighborenergy,temp)>数学。random()){
currentSolution=new Tour(newSolution.ゲットゥール());
}
// 見つかった最良の解決策を追跡する
if(currentSolution.getDistance()<ベスト。getDistance()){
best=新しいツアー(currentSolution.ゲットゥール());
}
// クールシステム
temp*=1-coolingRate;
}
システム。出ろprintln(“最終解の距離:”+best.getDistance());
システム。出ろprintln(“Tour:”+best);
}
}
出力
最終解距離:911
ツアー: |180, 200/200, 160/140, 140/180, 100/180, 60/200, 40/160, 20/120, 80/100, 40/60, 20/20, 20/20, 40/60, 80/100, 120/40, 120/20, 160/60, 200/80, 180/100, 160/140, 180|
結論
この例では、ランダムに生成された最初のルートの半分以上の距離を得ることができました。 これは、この比較的単純なアルゴリズムが特定のタイプの最適化問題に適用されたときにどれほど便利であるかを示すことを願っています。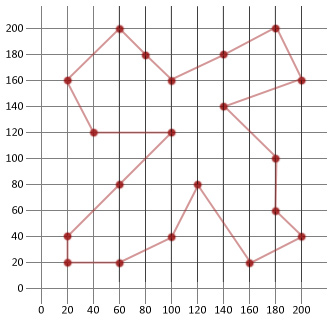
著者
 こんにちはい。
こんにちはい。私は技術とビジネスを愛する英国の開発者です。 ここでは、私に興味のあるものについての記事やチュートリアルを見つけることができます。 あなたは私を雇うか、私についての詳細を知りたい場合は、私の私についてのページ
に頭の上に私についての詳細を知りたいです