
単位桁を識別するという概念については、まず周期性の概念に慣れる必要があります。 任意の数の周期性は、最後の桁と、それらが特定の定義された方法でどのように表示されるかについてです。 このことをクリアする例を見てみましょう:
2の周期性チャートは次のとおりです:
21 =2
22 =4
23 =8
24=16
25=32
上記をよく見てください。 2が毎回それ自身の自己で乗算されると、最後の桁が変化することがわかります。 4番目の乗算では、25は21と同じ単位桁を持ちます。 これは、2の周期性が4であることを示しています。
周期性表:
数値の周期性表は以下のように与えられています:
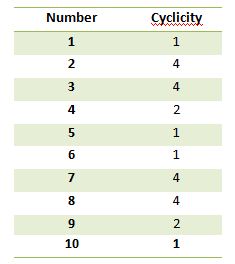
上記をどのように把握しましたか? 乗算し、自分自身のために参照してください。 それは良い習慣です。
ここで、周期性の概念を使って数値の単位桁を計算しましょう。
式4993の単位桁は何ですか?
今、私たちはこれを解決するための二つの方法を持っていますが、我々はそれを解決するための最良の方法を選択します。
私たちは4の周期性が2であ:
41 =4
42 =16
43 =64
44 =256
上から、4の周期性が2であることは明らかである。 今、周期数、すなわち2で与えられた力、すなわち993を2で割ると、残りは1になりますので、4が力の1に上がったときの答えは4です。したがって、この場合の単位桁は4です。
あなたがトピックを学んだかどうかを確認するために、このような任意の数を考え、その単位桁を計算し、電卓の助けを借りてそれを確認してくださ
注:どのような場合でも剰余がゼロになると、単位桁はサイクリシティ数
の最後の桁になります。aは与えられた数であり、サイクリシティ数は上の図に示されています。
別の例を解くことができます:
数7295X3158の単位の場所の数字は
A.7
B.2
C.6
Dです。 4
溶液
7の周期性表は次のとおりです:
71 =7
72 =49
73 = 343
74 = 2401
295を4で割り、残りは3です。
したがって、7295の最後の桁は73の最後の桁、つまり3に等しくなります。
3の周期性表は以下の通りである:
31 =3
32 =9
33 = 27
34 = 81
35 = 243
158を4で割り、残りは2です。 したがって、最後の桁は9になります。
したがって、(7925X3158)の単位の桁は、7925の単位の位置にある桁の積の単位の桁であり、3158=3*9=27です。 したがって、オプション1が答えです。
