私はCourseraでAndrew Ngの人気のある機械学習コースを始めました。 最初の週は、少なくとも数年前から微積分に触れていない人にとっては、多くのことをカバーしています
- コスト関数(平均差の二乗)
- 勾配降下
- 線形回帰
私はそれぞれについて詳細に話し、それらがどのように一緒に収まるかを実証するためのpythonコードと一緒に話します。
編集月4日: 直感、手作業で計算する方法、2つの異なるPython実装など、ここでコスト関数がどのように機能するかに焦点を当てたフォローアップを公開しました。 私は勾配降下を行い、すぐに線形回帰のためにそれらをまとめることができます。
モデル表現
まず、ほとんどの機械学習アルゴリズムの目標は、モデルを構築することです。 たとえば、家の大きさと販売価格を含む一連の住宅データに基づいてモデルを訓練するとします。 モデルを訓練することによって、私はそれに基づいてのためのあなたの家を販売できるかどの位の推定値をであるサイズ与えることができる。 これは回帰問題の例です—いくつかの入力が与えられた場合、連続した出力を予測したいと考えています。
この仮説は、通常、次のように提示されます

シータ値はパラメータです。
仮説をどのように視覚化するかのいくつかの簡単な例:
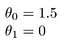
これにより、h(x)=1.5+0xが得られます。 0xは傾きがないことを意味し、yは常に定数1.5になります。 これは次のようになります:

どうですか
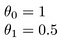

モデルを作成する目的は、h(x)がトレーニングデータxとyのyに近いように、パラメータまたはシータ値を選択することです。 だからこのデータのために
x =
y =

線形回帰を使用して最適な行を見つけようとします。 始めよう
コスト関数
データセットのパラメータを最小化する関数が必要です。 よく使用される一般的な関数の1つは、推定量(データセット)と推定値(予測)の差を測定する平均二乗誤差です。 これは次のようになります:

トラックの計算をもう少し簡単にするために、方程式を少し調整することができます。 私たちは最終的に:
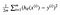
このconst関数を次のデータに適用しましょう:

今のところ、我々はいくつかのシータ値を計算し、手でコスト関数をプロットします。 この関数は(0,0)を通過するので、thetaの単一の値のみを見ています。 ここからは、コスト関数をJ(Θ)と呼びます。
J(1)の場合、0が得られます。 驚くことではありません—J(1)の値は、データに完全に適合する直線を生成します。 Jはどうですか?(0.5

MSE関数は0.58の値を与えます。 これまでの両方の値をプロットしてみましょう:
J(1) = 0
J(0.5)=0.58

私は先に進み、J(Θ)のいくつかの値を計算します。

点をうまく結合すれば…

theta=1の場合、コスト関数は最小であることがわかります。 これは理にかなっています—私たちの初期データは、傾きが1の直線です(上の図のオレンジ色の線)。
勾配降下法
私たちは、上記の試行錯誤によってJ(Θ)を最小化しました—ちょうど多くの値を試して、結果のグラフを視覚的に検査します。 より良い方法がなければなりませんか? キュー勾配降下。 勾配降下法は、関数、この場合は平均二乗誤差コスト関数を最小化するための一般的な関数です。
Gradient Descentは基本的に私たちが手作業でやっていたことを行います—シータ値、またはパラメータを少しずつ変更し、うまくいけば最小になるまで変更します。
まず、theta0とtheta1を任意の2つの値に初期化し、両方の値を0とし、そこから移動します。 形式的には、アルゴリズムは次のようになります:

ここで、α、αは学習率、または最小値に向かってどのくらい速く移動したいかです。 しかし、αが大きすぎると、オーバーシュートすることができます。

すべてをまとめる—線形回帰
すぐに要約する:
仮説があります:

これは私たちのトレーニングデータに適合する必要があります。 平均二乗誤差のようなコスト関数を使用することができます:

:

これは私たちの最初の機械学習アルゴリズム、線形回帰につながります。 作業線形回帰モデルを作成するために解決する必要があるパズルの最後の部分は、コスト関数の部分派生です:
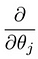
これは次のようになります:
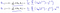
これは線形回帰を与えます!
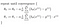
道の理論では、私は次の記事でpythonでこのロジックを実装するために行くでしょう。
編集5月4日:直感、手で計算する方法、2つの異なるPython実装など、コスト関数がここでどのように機能するかに焦点を当てたフォローアップを公開し 私は勾配降下を行い、すぐに線形回帰のためにそれらをまとめることができます。