熱伝導率

固体の熱伝導率は、それらが導体であるかどうかによって異なる性質のものである。 自由電荷を持たない誘電体では、熱エネルギーはフォノンによって伝達される。 結晶格子中の原子の集団振動は変位波の形をとり、その干渉は波パケット、すなわちフォノンを生成する。 変位波は、屈折率の変化として現れることができる密度の変動をもたらす。 屈折率が平均体積値と異なる領域を波が通過すると、熱運動のエネルギーを運ぶその後の変位波が散乱される。

散乱が強いほど、原子の格子内の平均位置からの最大偏差、すなわちTが高くなります。 これは、結晶誘電体の熱伝導率がかなり高い温度で減少するという実験的に確立された事実を説明しています：π1/T（図1）。

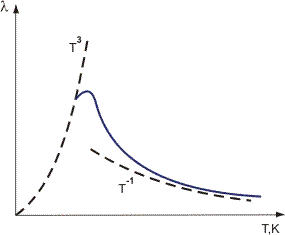
図1. 結晶誘電体の温度による熱伝導率の変化。

デバイは、量子力学的概念の枠組みの中で、低Tでのσ(T)変動のピークのような性質についての洞察を与えた。 彼は剛体双極子としての分子の概念に基づいて誘電体の双極子理論を詳述した。 このモデルでは、デバイは固体中の原子振動の最大周波数に比例する、いわゆるデバイ温度θ dの概念を導入した。 ほとんどの物質では、σ dは室温よりも低いか、または室温に近い（例外はσ d=1850Kのダイヤモンドおよびσ d=1160Kのベリリウムである）。

固体の量子論では、結晶格子は、最も単純な運動論の演繹が適用されるフォノンガスで満たされた体積とみなされます

ここで、cはフォノンガスの熱容量と一致する誘電体の熱容量、vは音速にほぼ等しいフォノンの平均速度、はフォノンの平均自由経路である。 ある有限値の存在は、フォノン上、結晶格子の欠陥、特に試料全体の粒界上のフォノン散乱の結果である。 温度依存性θ(T)は、およびcの温度依存性によって決定されます。

デバイ温度θ dを大幅に超える高温では、を制限する基本的なメカニズムは、結晶中の原子振動の非調和性によるフォノン-フォノン散乱である。 熱抵抗のフォノン-フォノン機構（（1/π）は熱抵抗係数として知られている）は、フォノン流れの遅延と準運動量のかなりの変化をもたらす遷移のためにのみ実現可能である。 Tが高いほど、が減少する遷移の確率が高くなります:(1/T）。 T>θ dの熱容量cは温度とともにわずかに増加するだけなので、θ1/T。

デバイ温度より低い温度T<<θ dでは、フォノン-フォノン散乱によって決定される平均自由経路の長さが大きくなり、exp θ d/Tとなり、原則として結晶Rの大きさに限定される。 したがって、T→0では、熱伝導率θはT3に比例して減少しなければならない。 熱伝導率がピークを有する温度は、≤Rから決定され、これは一般にT≤0.05≤dに相当する。

この理論は、長距離秩序を持たない非晶質物質、すなわち”結晶”のサイズが原子サイズのオーダーである非晶質物質の熱伝導率の挙動も説明しています。 これにより、これらの物質の”境界”での散乱は、すべてのTおよび≤constで優勢でなければならない。 アモルファス物質の熱伝導率≤T3低温では、中程度および高温では、熱容量に比例してわずかに成長しなければならないT>θ d。

このすべては、実際の結晶誘電体における依存性σ(T)の定性的な説明を提供するが、他の元素およびそれ自身の同位体の原子不純物による定格子からの偏差を考慮していない。 高温で熱輸送に不純物によって提供される抵抗は温度の独立者である。 これにより、温度による熱伝導率の変化から結晶純度の程度を推定することが可能になる。 同じ事実は、ガラスが結晶中の不純物とみなされる場合、天然鉱物中のガラス状物質と結晶物質との間の分布を決定することを可能にする。

金属の熱伝導率は、電流キャリア、すなわち伝導電子の運動と相互作用に依存する。 一般的に、熱伝導率λの金属の合算値で格子フォノン)λph、電子λe部品、λ=λe+λph、常温で、原則としてλe>>λph.

自由電子の流れにガスの単純な速度論を適用し、自由経路の長さが速度に依存しないと仮定すると、理論は次のことを意味します

ここで、eは電子電荷、K Boltzrnann定数、およびπは電気伝導率である。 厳密な量子力学理論は、同様の関係を提供します,

どちらの式においても，広い温度範囲での熱伝導率σの電子部分の電気伝導率σに対する比は，Ｗｉｅｄｅｍａｎｎ-Ｆｒａｎｚの法則σ／σ＝ＬＴ（ｌはＬｏｒｅｎｔｚ数）に従った温度に比例するように見える。 この法則は、測定された電気伝導度からθ eを計算するために使用されます。 しかし、電子-フォノン相互作用が優勢であるとき、それはσ d以下の温度で違反される（σはT−5としてtの減少とともに成長し、leはT−2としてよりわずかに変化する）。

実験結果は、原則として、高温での金属の熱伝導率は温度のわずかに減少する関数であることを示しています。 しかし、多くの例外があります。 したがって，鉄の熱伝導率は温度とともに強く減少し，タンタルとニオブは正の温度係数を示す。

興味深いのは、固体の融点Tmなどの単一の特性温度について、異なる物質の熱伝導率の係数を比較する試みです。 このように、Missenardによって行われた実験データの統計処理は、融点σ(T=Tm)=σ mにおける金属の熱伝導率はσに比例し、T=Tmにおける誘電結晶の熱伝導率はに比例し、mは分子量、Nは化学式中の原子数、σは密度、融点Tmはケルビン単位であることを示している。

半導体の熱輸送は、フォノンと電子成分が同じように不可欠であるため、誘電体や金属よりも複雑です。 複雑さのもう一つの理由は、不純物、バイポーラ拡散、および熱伝達に対する他のほとんど研究されていない要因のかなりの効果である。

固体の熱伝導率に及ぼす圧力の影響は、pで成長する多くの金属について、良好な精度で直線的であると仮定することができます。

固体の熱伝導率に及ぼす気孔率の影響については、多孔質媒体を参照してください。