電場Eは常にスカラーポテンシャル関数の勾配として表すことができます
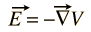
磁場Bには一般的なスカラーポテンシャルはありませんが、ベクトル関数のカールとして表すことができます
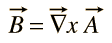
この関数Aには”ベクトルポテンシャル”という名前が与えられていますが、スカラーポテンシャルのように仕事に直接関連するものではありません。
ベクトルポテンシャルはアンペアの法則と一致するように定義されており、電流iまたは電流密度j(磁場の源)のいずれかで表すことができます。 様々なテキストでは、この定義は次の形式をとります
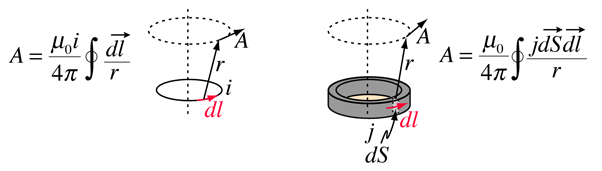
ベクトル電位の1つの理論的根拠は、与えられたソース電流幾何学から直接磁場を計算するよりもベクトル電位を計算する方が簡単である可能性があるということである。 その共通の適用は電磁波のアンテナ理論そして記述にあります。
磁場BはAのカールとして定義され、ベクトル恒等式によって勾配のカールは同じようにゼロであるため、スカラー関数の勾配として表現できる任意の関数は、それから得られたBの値を変更することなくAに追加することができる。 つまり、a’はa whereに自由に置き換えることができます
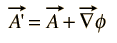
このような変換はゲージ変換と呼ばれ、電磁理論における特定のタイプの計算を有利にするために使用されてきた多くの”ゲージ”が存在している。