SSIMは、2004年のIEEE論文Image Quality Assessment:From Error Visibility to Structural Similarityで初めて導入されました。 要約は、提案されたシステムの背後にあるアイデアに良い直感を提供します,
知覚的画質を評価するための客観的な方法は、伝統的に、人間の視覚系の様々な既知の特性を用いて、歪んだ画像と参照画像との間の誤差(差)の可視性を定量化することを試みた。 人間の視覚はシーンから構造情報を抽出するために高度に適応されているという仮定の下で,構造情報の劣化に基づく品質評価のための代替補完的なフレームワークを導入した。
要約:著者は2つの本質的なポイントを作る,
- ほとんどの画質評価技術は、参照画像とサンプル画像との間の誤差を定量化することに依存しています。 一般的なメトリックは、(例えば、平均二乗誤差を使用して)サンプルと参照画像との間の対応する画素のそれぞれの値の差を定量化することである。
- 人間の視覚システムは、シーンから構造情報を識別することができるため、参照から抽出された情報とサンプルシーンの違いを識別することができます。 したがって、この動作を複製するメトリックは、サンプルと参照画像の区別を伴うタスクでより効果的に実行されます。
構造類似度指数(SSIM)メトリックは、画像から3つの主要な特徴を抽出します:
- 輝度
- コントラスト
- 構造
二つの画像の比較は、これら3つの特徴に基づいて行われます。
以下の図1は、構造類似度測定システムの配置と流れを示しています。 信号Xと信号Yは、参照画像とサンプル画像を参照します。

しかし、この指標は何を計算しますか?
このシステムは、-1と+1の間の値である2つの与えられた画像間の構造類似度指数を計算します。 +1の値は、2つの指定された画像が非常に似ているか同じであることを示し、-1の値は2つの指定された画像が非常に異なっていることを示します。 多くの場合、これらの値は、極端な値が同じ意味を保持する範囲に調整されます。
ここで、これらの特徴が数学的にどのように表現され、最終的なSSIMスコアにどのように貢献するかを簡単に見てみましょう。
- 輝度:すべてのピクセル値を平均化して輝度を測定します。 そのσ(Mu)で表され、式は以下に与えられます,
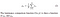
- コントラスト: これは、すべてのピクセル値の標準偏差(分散の平方根)を取ることによって測定されます。 これはσ(sigma)で表され、以下の式で表されます,
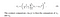
- 構造: 構造比較は連結式(詳細は後述)を使用して行われますが、本質的には、入力信号を標準偏差で分割して、結果が単位標準偏差を持つようにして、より堅牢な比較を可能にします。
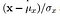
であるため、3つのパラメータの背後にある数学的直感を確立しました。 しかし、上のホールド! 私たちはまだもう少し、数学で行われていません。 私たちが今欠けているのは、これらのパラメータ上の2つの与えられた画像を比較できる比較関数、そして最後にそれらをすべて組み合わせた組み合 ここでは、比較関数を定義し、最後に、類似度指数値
- 輝度比較関数を生成する組み合わせ関数を定義します:以下に示す関数l(x,y)によって定義されます。 σ(mu)は、与えられた画像の平均を表します。 xとyは、比較される2つの画像です。
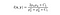
ここで、c1は分母が0になったときの安定性を確保するための定数です。 C1は次式で与えられます,
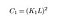
更新:この記事を通して、この方程式のK定数とL定数は何かを調べていませんでした。 ありがたいことに、読者はコメントでそれを指摘したので、この記事をもう少し参考にするために、ここでそれらを定義します。
Lはピクセル値のダイナミックレンジです(標準の8ビット画像を扱っているため、255に設定します)。 ここでは、さまざまな画像タイプとその意味についての詳細を読むことができます。
K1、K2は単なる通常の定数であり、そこには何もありません!
- コントラスト比較関数:以下に示す関数c(x,y)によって定義されます。 σは、与えられた画像の標準偏差を示します。 xとyは、比較される2つの画像です。
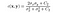
ここで、C2は次式で与えられます,
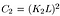
- 構造比較関数:これは、以下に示す関数s(x、y)によって定義されます。 σは、与えられた画像の標準偏差を示します。 xとyは、比較される2つの画像です。
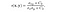
ここで、θ(xy)は次のように定義されます,
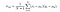
そして最後に、SSIMスコアは次のように与えられます,

ここで、α<5 2 6 2>0、β<5 2 6 2>0、γ<5 2 6 2>0は、各メトリックの相対的重要性を示す。 式を単純化するために、α=β=γ=1およびC3=C2/2と仮定すると、次のようになります,
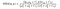
しかし、プロットのねじれがあります!上記の式を使用してSSIMを実装することはできますが、著者が説明しているように、すぐに使用できる実装ほどうまくいかない可能性があります。
,
画質評価では、SSIMインデックスをグローバルではなくローカルに適用すると便利です。 第一に、画像統計的特徴は、通常、非常に空間的に非定常である。 第二に、局所的な画像統計に依存してもしなくてもよい画像の歪みは、空間変形であってもよい。 第三に、典型的な視距離では、画像内の局所領域のみが、一度に人間の観察者によって高解像度で知覚されることができる(HVSのfoveation特徴のために)。 そして最後に、局所的な品質測定は、画像の空間的に変化する品質マップを提供することができ、画像の品質劣化に関するより多くの情報を提供し、
: 上記の指標をグローバルに(つまり、画像全体に一度に)適用するのではなく、地域的に(つまり、画像の小さなセクションで、全体の平均を取る)指標を適用す
この方法は、多くの場合、平均構造類似度指数と呼ばれています。
このアプローチの変更により、式も同じことを反映するように変更する必要があります(このアプローチはより一般的であり、コードの説明に使用されます)。
(注:以下のコンテンツが少し圧倒的に見える場合は、心配しないでください! あなたがそれの要点を得れば、コードを通過することはあなたにはるかに明確な考えを与えるでしょう。)
著者は、画像全体にわたってピクセルごとに移動する11×11円対称ガウス計量関数(基本的には、ガウス分布から値が導出される11×11行列)を使用します。 各ステップで、ローカル統計とSSIMインデックスがローカルウィンドウ内で計算されます。 現在、メトリックをローカルで計算しているため、数式は次のように改訂されています,
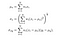
ここで、wiはガウス重み付け関数です。
これを少し直感的ではないと見つけた場合、心配はありません! いくつかの数学的なトリックの助けを借りて必要な値を計算するために使用される乗数としてwiを想像すれば十分です。
画像全体で計算が実行されると、すべてのローカルSSIM値の平均を取得し、グローバルSSIM値に到達します。
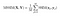
最終的に理論で行われました! 今すぐコードに!