
この記事では、指向勾配のヒストグラム(HOG)特徴記述子の詳細を学びます。 内部に何があるのか、この記述子がOpenCV、MATLAB、およびその他のパッケージによって内部的にどのように計算されるのかを学びます。
この記事は、私が画像認識と物体検出について書いているシリーズの一部です。
このシリーズのチュートリアルの完全なリストを以下に示します:
- 従来のコンピュータビジョン技術を用いた画像認識 : パート1
- 配向勾配のヒストグラム:パート2
- 画像認識のためのコード例:パート3
- より良い眼検出器のトレーニング:パート4a
- 伝統的なコンピ深層学習を用いた認識 : パート6
- ニューラルネットワークの紹介
- フィードフォワードニューラルネットワークの理解
- 畳み込みニューラルネットワークを用いた画像認識
- 深層学習を用いた物体検出:その一部7
多くの多くのものは困難で神秘的に見えます。 しかし、あなたがそれらを解体するのに時間がかかると、謎は習得に置き換えられ、それが私たちが後にしているものです。 あなたは初心者であり、ハードと神秘的なコンピュータビジョンを見つけている場合は、ちょうど次の
Qを覚えています:どのように象を食べますか?
: 一度に一口!
機能記述子とは何ですか?
特徴記述子は、有用な情報を抽出し、無関係な情報を捨てることによって画像を単純化する画像または画像パッチの表現です。
通常、特徴記述子は、幅x高さx3(チャネル)のサイズの画像を長さnの特徴ベクトル/配列に変換します。HOG特徴記述子の場合、入力画像のサイズは64x128x3で、出力特徴ベクトルの長さは3780です。
HOG記述子は他のサイズでも計算できることに注意してくださいが、この記事では元の論文に記載されている数字にこだわっているので、具体的な例
これはすべて良い音ですが、”有用”とは何か、”無関係”とは何ですか? 「有用」を定義するには、それが何のために「有用」であるかを知る必要がありますか? 明らかに、特徴ベクトルは画像を表示する目的には有用ではありません。 しかし、画像認識や物体検出などの作業には非常に便利です。 これらのアルゴリズムによって生成された特徴ベクトルは、サポートベクターマシン(SVM)のような画像分類アルゴリズムに供給されたときに良好な結果
しかし、分類タスクにはどのような”機能”が役立つのでしょうか? 例を使用してこの点について説明しましょう。 シャツやコートのボタンを検出するオブジェクト検出器を構築したいとします。
ボタンは円形(画像では楕円形に見えることがあります)で、通常は縫製のためのいくつかの穴があります。 ボタンの画像に対してエッジ検出器を実行し、エッジ画像だけを見るだけでボタンであるかどうかを簡単に知ることができます。 この場合、エッジ情報は「有用」であり、色情報はそうではありません。 加えて、特徴はまた、識別力を有する必要がある。 たとえば、画像から抽出された優れた機能は、ボタンとコインや車のタイヤのような他の円形のオブジェクトとの違いを見分けることができるはず
HOG特徴記述子では、勾配の方向(配向勾配)の分布(ヒストグラム)が特徴として使用されます。 グラデーションの大きさはエッジとコーナー(急激な強度変化の領域)の周りに大きく、エッジとコーナーは平坦な領域よりもオブジェクトの形状に関する多くの情報を詰め込むことがわかっているため、画像の勾配(xおよびyの導関数)が便利です。
配向勾配のヒストグラムを計算するには?
このセクションでは、HOG機能記述子の計算の詳細について説明します。 各ステップを説明するために、画像のパッチを使用します。
ステップ1 : 前処理
先に述べたように、歩行者検出に使用されるHOG特徴記述子は、画像の64×128パッチで計算されます。 もちろん、画像は任意のサイズであってもよいです。 通常、複数のスケールのパッチは、多くの画像位置で分析されます。 唯一の制約は、分析されるパッチのアスペクト比が固定されていることです。 私たちの場合、パッチの縦横比は1:2である必要があります。 例えば、それらは、1 0 0×2 0 0、1 2 8×2 5 6、または1 0 0 0×2 0 0 0であってもよいが、1 0 1×2 0 5ではない。
この点を説明するために、サイズ720×475の大きな画像を示しました。 HOG機能記述子を計算するために、サイズ100×200のパッチを選択しました。 このパッチは画像から切り取られ、64×128にサイズ変更されます。 これで、この画像パッチのHOG記述子を計算する準備が整いました。

DalalとTriggsの論文では、前処理ステップとしてガンマ補正についても言及していますが、パフォーマンスの向上は軽微なので、ステップをスキップしています。
ステップ2:勾配画像を計算する
HOG記述子を計算するには、まず水平勾配と垂直勾配を計算する必要があります; 結局のところ、我々は勾配のヒストグラムを計算したい。 これは、以下のカーネルで画像をフィルタリングすることによって簡単に達成されます。
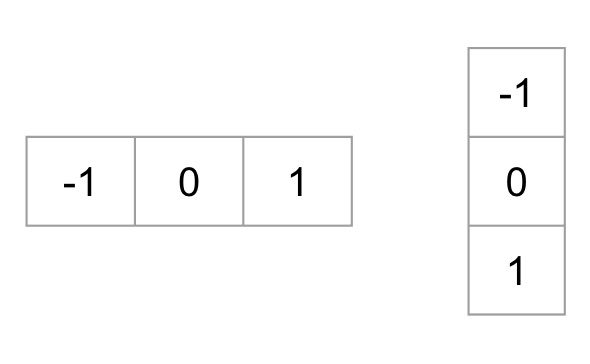
カーネルサイズ1のOpenCVでSobel演算子を使用することで、同じ結果を達成することもできます。
// C++ gradient calculation.// Read imageMat img = imread("bolt.png");img.convertTo(img, CV_32F, 1/255.0);// Calculate gradients gx, gyMat gx, gy;Sobel(img, gx, CV_32F, 1, 0, 1);Sobel(img, gy, CV_32F, 0, 1, 1);
# Python gradient calculation # Read imageim = cv2.imread('bolt.png')im = np.float32(im) / 255.0# Calculate gradientgx = cv2.Sobel(img, cv2.CV_32F, 1, 0, ksize=1)gy = cv2.Sobel(img, cv2.CV_32F, 0, 1, ksize=1)
次に、次の式を使用して勾配の大きさと方向を見つけることができます

OpenCVを使用している場合は、以下に示すように関数cartToPolarを使用して計算を行うことができます。
// C++ Calculate gradient magnitude and direction (in degrees)Mat mag, angle;cartToPolar(gx, gy, mag, angle, 1);
pythonの同じコードは次のようになります。
# Python Calculate gradient magnitude and direction ( in degrees )mag, angle = cv2.cartToPolar(gx, gy, angleInDegrees=True)
下の図はグラデーションを示しています。
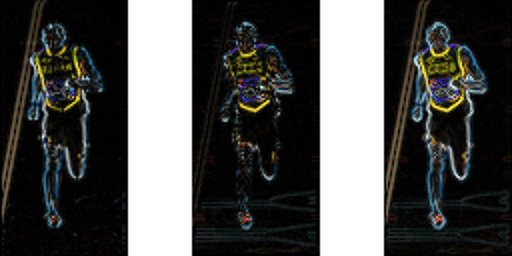
x勾配は垂直線で、y勾配は水平線で発生することに注意してください。 勾配の大きさは、これまでの強度の急激な変化がある場所で発生します。 地域が滑らかであるとき、それらのどれも発射しません。 画像として表示される方向はあまり伝わりませんので、グラデーションの方向を示す画像は意図的に省略しています。
グラデーション画像では、必須ではない多くの情報(一定の色の背景など)が削除されましたが、輪郭が強調表示されました。 言い換えれば、あなたはグラデーション画像を見て、まだ簡単に絵の中に人がいると言うことができます。
すべてのピクセルで、勾配は大きさと方向を持ちます。 カラー画像の場合、3つのチャンネルの勾配が評価されます(上の図に示すように)。 ピクセルにおける勾配の大きさは、3つのチャネルの勾配の大きさの最大値であり、角度は、最大勾配に対応する角度である。
ステップ3:8×8セルの勾配のヒストグラムを計算する

このステップでは、画像を8×8セルに分割し、8×8セルごとに勾配のヒストグラムを計算します。
すぐにヒストグラムについて学びますが、そこに行く前に、なぜ画像を8×8のセルに分割したのかを最初に理解しましょう。 特徴記述子を使用して画像のパッチを記述する重要な理由の1つは、コンパクトな表現を提供することです。 8×8の画像パッチには、8x8x3=192ピクセル値が含まれています。 このパッチの勾配には、ピクセルあたり2つの値(大きさと方向)が含まれており、最大8x8x2=128個の数字が加算されます。
このセクションの最後までに、これらの128個の数字が9個の数字の配列として格納できる9ビンのヒストグラムを使用してどのように表されるかを見ていきます。 表現がよりコンパクトであるだけでなく、パッチ上のヒストグラムを計算することで、この表現がノイズに対してより堅牢になります。 個々のグライデントにはノイズがあるかもしれませんが、8×8パッチを超えるヒストグラムでは、表現はノイズに敏感ではありません。
しかし、なぜ8×8パッチ? なぜ32×32ではないのですか? それは私達が捜している特徴のスケールによって知らされる設計選択である。 HOGは歩行者の検出のために最初に使用されました。 64×128にスケーリングされた歩行者の写真の8×8セルは、興味深い特徴(顔、頭の上など)をキャプチャするのに十分な大きさです。 ).
ヒストグラムは基本的に、角度に対応する9つのビン(数値)のベクトル(または配列)です0, 20, 40, 60 … 160.
画像内の8×8パッチを見て、グラデーションがどのように見えるかを見てみましょう。
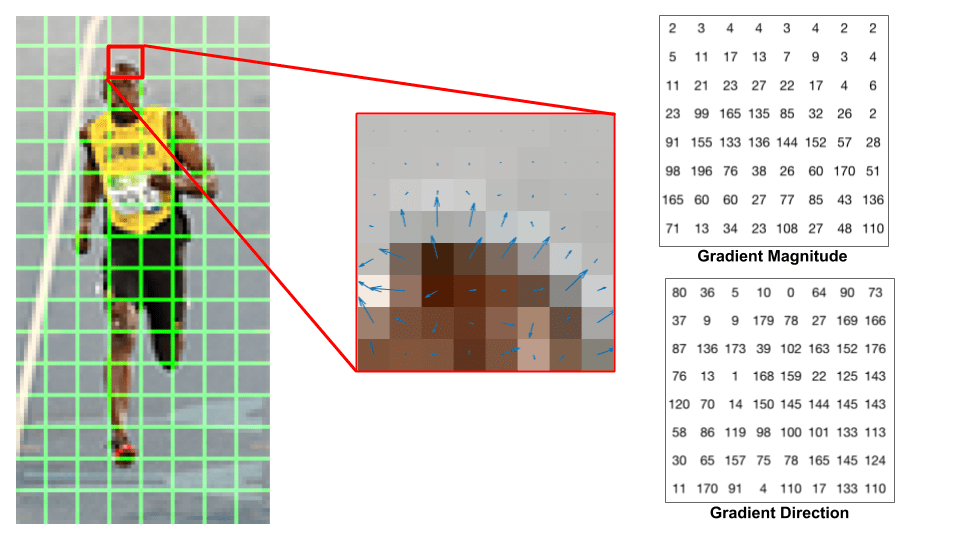
あなたがコンピュータビジョンの初心者であれば、中央の画像は非常に有益です。 これは、グラデーションを示す矢印で覆われた画像のパッチを示しています—矢印はグラデーションの方向を示し、その長さは大きさを示しています。 矢印の方向が強度の変化の方向を指しており、大きさがその差の大きさを示していることに注意してください。
右側には、8×8セルの勾配を表す生の数字があり、角度は0から360度ではなく0から180度の間にあります。 勾配と負の勾配は同じ数値で表されるため、これらは「符号なし」勾配と呼ばれます。 言い換えれば、勾配矢印とそれと反対の180度の矢印は同じとみなされます。 しかし、なぜ0–360度を使用しないのですか?
経験的には、歩行者の検出のために符号なし勾配が符号付き勾配よりも優れていることが示されています。 HOGのいくつかの実装では、署名付き勾配を使用するかどうかを指定できます。
次のステップは、これらの8×8セルに勾配のヒストグラムを作成することです。 ヒストグラムには、角度0、20、40…160に対応する9つのビンが含まれています。 次の図は、プロセスを示しています。 前の図と同じ8×8パッチの勾配の大きさと方向を見ています。
方向に基づいてビンが選択され、大きさに基づいて投票(ビンに入る値)が選択されます。 まず、青で囲まれたピクセルに焦点を当てましょう。 それは80度の角度(方向)と2の大きさを持っています。 したがって、2を5番目のビンに追加します。 赤を使用して囲まれたピクセルの勾配は、10度の角度と4の大きさを持っています。 10度は0と20の間の半分の方法であるため、ピクセルによる投票は2つのビンに均等に分割されます。
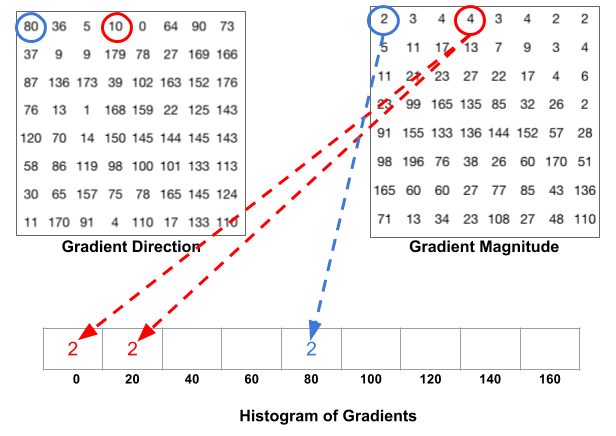
注意すべきもう一つの詳細があります。 角度が160度より大きい場合、それは160と180の間にあり、角度が0と180を同等にすることを知っています。 したがって、以下の例では、角度が165度のピクセルは、0度ビンと160度ビンに比例して寄与します。
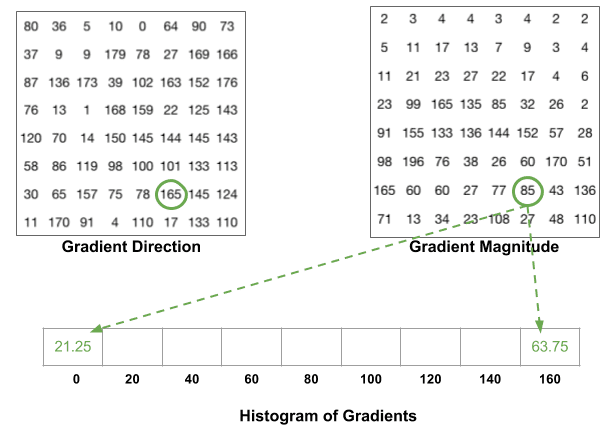
8×8セル内のすべてのピクセルの寄与は、9ビンのヒストグラムを作成するために加算されます。 上記のパッチでは、次のようになります
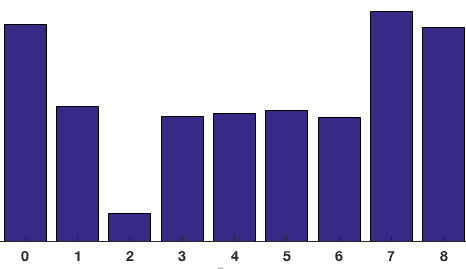
私たちの表現では、y軸は0度です。 ヒストグラムには0度と180度の近くに多くの重みがありますが、これはパッチではグラデーションが上または下を指していると言う別の方法です。
ステップ4 : 16×16ブロック正規化
前のステップでは、画像の勾配に基づいてヒストグラムを作成しました。 画像のグラデーションは、全体的な照明に敏感です。 すべてのピクセル値を2で割ってイメージを暗くすると、グラデーションの大きさが半分に変化するため、ヒストグラムの値は半分に変化します。
理想的には、記述子を照明の変動とは無関係にしたいと考えています。 言い換えれば、ヒストグラムを”正規化”して、照明の変動の影響を受けないようにしたいと考えています。
ヒストグラムがどのように正規化されるかを説明する前に、長さ3のベクトルがどのように正規化されるかを見てみましょう。
RGBカラーベクトルがあるとしましょう。 このベクトルの長さはsqrt sqrt sqrtです{128^2 + 64^2 + 32^2} = 146.64$. これはベクトルのL2ノルムとも呼ばれます。 このベクトルの各要素を146.64で除算すると、正規化されたベクトルが得られます。
ここで、要素が最初のベクトル2x=の2倍の値である別のベクトルを考えてみましょう。 正規化が元のRGBベクトルの正規化されたバージョンと同じになることを確認するために、自分で作業することができます。 ベクトルを正規化するとスケールが削除されることがわかります。
ベクトルを正規化する方法がわかったので、HOGを計算するときに、上の3×1ベクトルを正規化したのと同じ方法で9×1ヒストグラムを正規化することができると思うように誘惑されるかもしれません。 それは悪い考えではありませんが、より良い考えは16×16のより大きなサイズのブロックで正規化することです。
16×16ブロックには4つのヒストグラムがあり、連結して36×1要素ベクトルを形成することができ、3×1ベクトルを正規化するだけの方法で正規化することができる。 次に、ウィンドウを8ピクセル移動し(アニメーションを参照)、このウィンドウ上で正規化された36×1ベクトルが計算され、プロセスが繰り返されます。
ステップ5:HOG特徴ベクトルの計算
画像パッチ全体の最終特徴ベクトルを計算するには、36×1ベクトルを1つの巨大ベクトルに連結します。 このベクトルのサイズは何ですか?
- 16×16ブロックの位置を何個計算してみましょうか? 7つの水平位置と15の垂直位置があり、合計7×15=105の位置になります。
- 各16×16ブロックは36×1ベクトルで表されます。 したがって、それらをすべて1つのgaintベクトルに連結すると、36×105=3780次元ベクトルが得られます。
配向勾配のヒストグラムの可視化

画像パッチのHOG記述子は、通常、9×1の正規化されたヒストグラムを8×8細胞にプロットすることによって視覚化される。 側面の画像を参照してください。 あなたは、ヒストグラムの支配的な方向は、特に胴体と脚の周りに、人の形状をキャプチャすることがわかります。残念ながら、OpenCVでHOG記述子を視覚化する簡単な方法はありません。