나는 코 세라에서 앤드류 응의 인기있는 기계 학습 과정을 시작했습니다. 첫 주에는 적어도 몇 년 동안 많은 미적분을 다루지 않은 사람에게는 많은 것을 다룹니다.
- 비용 함수(평균 차이의 제곱)
- 그라디언트 디센트
- 선형 회귀
이 세 가지 주제는 많이 다루었습니다. 나는 자세히 각각에 대해 얘기하자,그들은 모두 함께 맞는 방법,일부 파이썬 코드를 보여.
5 월 4 일 편집: 나는 직관,손으로 계산하는 방법 및 두 개의 다른 파이썬 구현을 포함하여 비용 함수가 여기에서 어떻게 작동하는지에 초점을 맞춘 후속 조치를 발표했습니다. 그라디언트 디센트를 수행 한 다음 곧 선형 회귀를 위해 함께 가져올 수 있습니다.
모델 표현
첫째,대부분의 기계 학습 알고리즘의 목표는 모델을 구성하는 것입니다. 예를 들어,집 크기와 판매 가격을 포함하는 많은 주택 데이터를 기반으로 모델을 훈련한다고 가정 해 보겠습니다. 모형을 훈련해서,너가 그것에 기초를 두는을 위해 너의 집을 이는 크기 매출할 수 있는 까 얼마에 나는 너에게 견적을 줄 수 있는다. 이 회귀 문제의 예입니다-일부 입력 주어진,우리는 연속 출력을 예측하려고합니다.
가설은 일반적으로 다음과 같이 제시됩니다

세타 값은 매개 변수입니다.
가설을 시각화하는 방법에 대한 몇 가지 빠른 예:
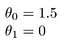
이 값은 다음과 같습니다. 0 엑스 는 기울기가 없음을 의미하며 항상 상수 1.5 가됩니다. 이 같은:

어때요
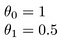

x =
y =

선형 회귀를 사용하여 가장 적합한 선을 찾으려고 노력할 것입니다. 시작합시다.
비용 함수
데이터 집합에 대한 매개 변수를 최소화하는 함수가 필요합니다. 자주 사용되는 일반적인 함수 중 하나는 추정기(데이터 세트)와 추정 값(예측)간의 차이를 측정하는 평균 제곱 오차입니다. 그것은 다음과 같이 보인다:

우리는 방정식을 조금 조정하여 트랙 아래로 계산을 좀 더 간단하게 만들 수 있습니다. 우리는 결국:
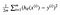
이 함수를 다음 데이터에 적용해 보겠습니다:

지금 우리는 몇 가지 세타 값을 계산하고 손으로 비용 함수를 그릴 것입니다. 이 함수는(0,0)을 통과하기 때문에 우리는 세타의 단일 값만 찾고 있습니다. 여기에서 비용 함수를 다음과 같이 참조 할 것입니다.0 을 얻습니다. 놀람-제이(1)의 값은 데이터에 완벽하게 맞는 직선을 생성합니다. 어떻게 제이(0.5)에 대해?

이 함수는 0.58 의 값을 제공합니다. 지금까지 두 값을 모두 플롯합시다.
제이(1) = 0
제(0.5)=0.58

나는 앞으로 몇 가지 더 많은 값을 계산할 것이다.

그리고 우리가 점들을 잘 결합한다면…

우리는 비용 함수가 세타=1 일 때 최소라는 것을 알 수 있습니다. 이것은 의미가 있습니다-우리의 초기 데이터는 기울기가 1 인 직선(위 그림의 주황색 선)입니다.
그라디언트 디센트
위의 시행 착오를 통해 많은 값을 시도하고 결과 그래프를 시각적으로 검사했습니다. 더 나은 방법이 있어야합니까? 큐 그라디언트 디센트. 그라디언트 디센트는 함수를 최소화하기위한 일반적인 함수이며,이 경우 평균 제곱 오차 비용 함수입니다.
그라디언트 디센트는 기본적으로 우리가 손으로 수행 한 작업을 수행합니다—세타 값 또는 매개 변수를 조금씩 변경하여 최소한 도달 할 때까지 변경하십시오.
우리는 0 과 1 을 두 개의 값으로 초기화하여 시작합니다. 공식적으로 알고리즘은 다음과 같습니다:

여기서,알파는 학습 속도 또는 최소값을 향해 얼마나 빨리 이동하기를 원합니다. 그러나 제 2 의 크기가 너무 크면 오버 슈트 할 수 있습니다.

모두 함께 가져 오기—선형 회귀
빨리 요약:
우리는 가설을 가지고있다:

우리는 훈련 데이터에 적합해야합니다. 우리는 비용 함수와 같은 평균 제곱 오류를 사용할 수 있습니다:

그라디언트 디센트를 사용하여 최소화 할 수 있습니다.:

우리의 첫 번째 기계 학습 알고리즘 인 선형 회귀로 이어집니다. 우리가 작업 선형 회귀 모델을 가지고 해결해야 할 퍼즐의 마지막 조각은 비용 함수의 부분 유도체이다:
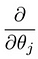
:
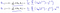
선형 회귀를 제공합니다!
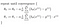
길에서 이론,나는 다음 게시물에서 파이썬에서이 논리를 구현하기 위해 갈 것이다.
5 월 4 일 편집:직관,손으로 계산하는 방법 및 두 가지 파이썬 구현을 포함하여 비용 함수가 어떻게 작동하는지에 초점을 맞춘 후속 조치를 발표했습니다. 그라디언트 디센트를 수행 한 다음 곧 선형 회귀를 위해 함께 가져올 수 있습니다.