특정 최적화 문제에 대한 최적의 솔루션을 찾는 것은 매우 어려운 작업이 될 수 있습니다,종종 거의 불가능. 이는 문제가 충분히 커지면 최적의 솔루션을 찾기 위해 엄청난 수의 가능한 솔루션을 검색해야하기 때문입니다. 심지어 현대 컴퓨팅 파워와 함께 고려해야 할 너무 많은 가능한 솔루션은 여전히 종종 있습니다. 이 경우 우리는 현실적으로 시간의 합리적인 길이 내에서 최적의 하나를 찾을 것으로 예상 할 수 없기 때문에,우리는 충분히 가까이 뭔가 정착해야.
일반적으로 가능한 솔루션이 많은 최적화 문제의 예는 여행 세일즈맨 문제입니다. 여행 판매원 문제와 같은 문제에 대한 해결책을 찾기 위해서는 합리적인 시간 내에 충분한 해결책을 찾을 수있는 알고리즘을 사용해야합니다. 이전 튜토리얼에서 우리는 우리가 유전자 알고리즘으로이 작업을 수행 할 수있는 방법을 살펴 보았다,유전자 알고리즘은 우리가 여행 세일즈맨 문제에 대한’충분히 좋은’솔루션을 찾을 수있는 한 가지 방법이지만,우리가 구현할 수있는 다른 간단한 알고리즘이있다 또한 우리에게 최적의 솔루션에 가까운을 찾을 수 있습니다. 이 튜토리얼에서 우리가 사용하는 알고리즘은’시뮬레이션 어닐링’입니다.
여행 세일즈맨 문제에 익숙하지 않은 경우 계속하기 전에 이전 자습서를 살펴 볼 가치가 있습니다.
시뮬레이션 어닐링이란?
먼저,시뮬레이션 어닐링이 어떻게 작동하는지,특히 여행 세일즈맨 문제에 대한 해결책을 찾는 것이 왜 좋은지 살펴 보겠습니다. 시뮬레이션 된 어닐링 알고리즘은 원래 금속 작업에서의 어닐링 과정에서 영감을 얻었습니다. 어닐링은 가열 및 내부 구조의 변화로 인해 물리적 특성을 변경하기 위해 재료를 냉각 포함한다. 금속이 냉각됨에 따라 새로운 구조가 고정되어 결과적으로 금속이 새로 얻은 특성을 유지합니다. 시뮬레이션 된 어닐링에서 우리는이 가열 과정을 시뮬레이션하기 위해 온도 변수를 유지합니다. 우리는 처음에 그것을 높게 설정 한 다음 알고리즘이 실행될 때 천천히’냉각’할 수 있습니다. 이 온도 변수가 높지만 알고리즘은 더 많은 빈도로 현재 솔루션보다 더 나쁜 솔루션을 수용 할 수 있습니다. 이렇게 하면 알고리즘이 실행 초기에 발견된 모든 로컬 최적값에서 벗어날 수 있습니다. 온도가 감소되는 때 이렇게 더 나쁜 해결책을 받아들이기의 기회는 이다,그런 까닭에 산법을 희망하는,최적 해결책에 가깝것이 발견될 수 있는 수색 공간의 지역에 점차적으로 안으로 초점을 맞추는 허용한. 이 점진적인’냉각’프로세스는 시뮬레이션 된 어닐링 알고리즘을 수많은 로컬 최적화를 포함하는 큰 문제를 처리 할 때 최적의 솔루션에 가까운 것을 찾는 데 현저하게 효과적으로 만듭니다. 여행 세일즈맨 문제의 본질은 그것을 완벽한 예로 만듭니다.
시뮬레이션 어닐링의 장점
간단한 언덕 산악인 같은 것을 통해 시뮬레이션 어닐링을 구현하는 실제 이점이 있는지 궁금 할 것이다. 언덕 등반 좋은 솔루션을 찾는 놀라울 정도로 효과적일 수 있습니다,하지만 그들은 또한 로컬 최적화에 갇혀 얻을 경향이 있다. 우리가 이전에 결정했듯이,시뮬레이션 된 어닐링 알고리즘은이 문제를 피하는 데 탁월하며 평균적으로 대략적인 글로벌 최적 조건을 찾는 데 훨씬 좋습니다.
더 나은 이해를 돕기 위해 기본 언덕 등반 알고리즘이 지역 최적화에 걸리기 쉬운 이유를 빠르게 살펴 보겠습니다.
언덕 산악인 알고리즘은 단순히 현재의 솔루션보다 더 나은 이웃 솔루션을 받아 들일 것입니다. 언덕 산악인이 더 좋은 이웃을 찾을 수 없을 때,그것은 멈 춥니 다.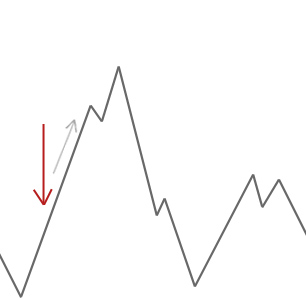
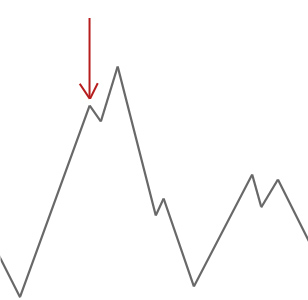
위의 예에서 우리는 빨간색 화살표에서 우리의 언덕 산악인을 시작하고 첫 번째 하강하지 않고 더 높은 올라갈 수없는 지점에 도달 할 때까지 언덕을 그것의 방법을 작동합니다. 이 예에서 우리는 그것이 지역 최적에 갇혀 있다는 것을 분명히 볼 수 있습니다. 이것이 현실 세계의 문제라면 우리는 검색 공간이 어떻게 보이는지 알지 못할 것입니다 불행히도 우리는이 솔루션이 글로벌 최적에 가까운 곳인지 여부를 말할 수 없을 것입니다.
시뮬레이션 어닐링은 이것과 약간 다르게 작동하며 때때로 더 나쁜 해결책을 받아들입니다. 시뮬레이션 된 어닐링의 이러한 특성은 그렇지 않으면 갇혀있을 수있는 모든 지역 최적화에서 뛰어 내리는 데 도움이됩니다.
수용 함수
알고리즘이 어떤 솔루션을 수용할지 결정하여 이러한 로컬 최적화를 피할 수있는 방법을 더 잘 이해할 수 있는지 살펴 보겠습니다.
먼저 이웃 솔루션이 현재 솔루션보다 더 나은지 확인합니다. 그것이 인 경우에,우리는 그것을 무조건적으로 받아들입니다. 그러나 이웃 솔루션이 더 좋지 않은 경우 몇 가지 요인을 고려해야합니다. 첫째,이웃 솔루션이 얼마나 더 나쁜지,둘째,우리 시스템의 현재’온도’가 얼마나 높은지. 높은 온도에서 시스템은 더 가능성이 더 나쁜 솔루션을 받아들입니다. 기본적으로 에너지 변화(솔루션의 품질)가 작을수록 온도가 높을수록 알고리즘이 솔루션을 수용 할 가능성이 높아집니다.
알고리즘 개요
알고리즘은 어떻게 보입니까? 음,가장 기본적인 구현에서는 매우 간단합니다.
- 먼저 초기 온도를 설정하고 임의의 초기 솔루션을 만들어야합니다.
- 그런 다음 정지 조건이 충족 될 때까지 루핑을 시작합니다. 일반적으로 시스템이 충분히 냉각되었거나 충분한 솔루션이 발견되었습니다.
- 여기에서 우리는 우리의 현재 솔루션에 작은 변화를 만들어 이웃을 선택합니다.
- 그런 다음 해당 이웃 솔루션으로 이동할지 여부를 결정합니다.
- 마지막으로 온도를 낮추고 루프를 계속합니다.
온도 초기화
더 나은 최적화를 위해 온도 변수를 초기화 할 때 현재 솔루션에 대한 거의 모든 이동을 허용하는 온도를 선택해야합니다. 이 알고리즘에게 더 나은 냉각하고 더 집중 지역에 정착하기 전에 전체 검색 공간을 탐색 할 수있는 기능을 제공합니다.
예제 코드
이제 우리가 알고있는 것을 사용하여 기본 시뮬레이션 어닐링 알고리즘을 만든 다음 아래의 여행 세일즈맨 문제에 적용하겠습니다. 우리는이 튜토리얼에서 자바를 사용하는거야,하지만 논리는 희망 당신의 선택의 어떤 언어로 복사 할 수있을만큼 간단해야한다.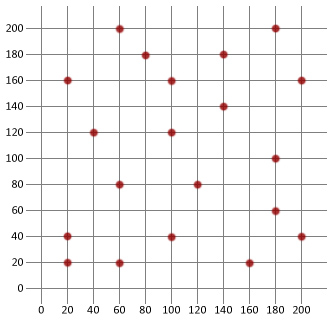
먼저 우리는 우리의 여행 세일즈맨의 다른 목적지를 모델링하는 데 사용할 수있는 도시 클래스를 만들어야합니다.
도시.자바
*도시.이 예제에서는 다음과 같은 방법을 사용합니다.:::::::::::::;
//무작위로 배치 된 도시
공공 도시(){
이.수학.무작위()*200);
이.수학.인기 동영상()*200);
}
// 이 예제에서는 다음과 같은 방법을 사용합니다.8701>이.예=예;
}
// 이 작업을 수행하는 방법은 다음과 같습니다.엑스;
}
// 이 작업을 수행하는 방법은 다음과 같습니다.와이;
}
// 주어진 도시까지의 거리를 가져옵니다.
공공 이중 거리(도시 도시){-도시.());
지능 거리=수학.-도시.(8701>이중 거리=수학.이 문제를 해결하는 데 도움이되는 몇 가지 방법이 있습니다.이 문제를 해결하는 데 도움이되는 몇 가지 방법이 있습니다.();
}
}
다음은 도시를 추적 할 수있는 클래스를 만들 수 있습니다.
투어매니저.자바
*투어 관리자.자바
*투어의 도시를 보유
*/
패키지 사;
가져 오기 자바.유틸리티어레일리스트는;이 응용 프로그램을 사용하면 다음과 같은 작업을 수행 할 수 있습니다.>();
// 대상 도시
공공 정적 무효 추가 도시(도시 도시){
목적지 도시를 추가합니다.추가(도시);
}
// 이 예제에서는 다음과 같은 방법을 사용합니다.가져 오기(색인);
}
// 대상 도시의 수를 가져옵니다
공공 정적 인 숫자(){
반환 목적지 도시.크기();
}
}
이제 여행 세일즈맨 투어를 모델링 할 수있는 클래스를 만들 수 있습니다.
투어.자바
*둘러보기.자바
*모든 도시를 통해 후보 투어를 저장
*/
패키지 사;
가져 오기 자바.유틸리티이 문제를 해결하려면 다음을 수행하십시오.유틸리티2015 년 11 월 15 일(토)~2015 년 11 월 15 일(일)>();
// 이 예제에서는 다음과 같은 방법을 사용합니다.:::::::::::::이 문제를 해결하는 방법은 다음과 같습니다.추가(널);
}
}
// 다른 투어에서 투어를 구성
공공 투어(배열 목록 투어){
이.투어=(배열 목록)투어.복제();
}
// 반환 투어 정보
공개 배열 목록 겟투어(){
반환 투어;
}
// 모든 목적지 도시를 반복하여 투어
에 추가합니다.이 예제에서는 다음과 같이 설명합니다.쩐쨀챌쩌쩌쩔채.));
}
// 투어
컬렉션을 무작위로 재정렬합니다.셔플(투어);이 예제에서는 다음과 같은 방법을 사용합니다.:::::::::::(투어 위치);
}
// 투어 내의 특정 위치에 도시를 설정합니다.설정(투어 위치,도시);
//투어가 변경된 경우 피트니스 및 거리
거리를 재설정해야합니다.= 0;
}
// 이 경우 투어의 총 거리를 얻을 수 있습니다.이 경우 투어의 총 거리를 얻을 수 있습니다.이 경우 투어의 총 거리를 얻을 수 있습니다.이 경우 투어의 총 거리를 얻을 수 있습니다.이 경우 투어의 총 거리를 얻을 수 있습니다.이 경우 투어의 총 거리를 얻을 수 있습니다.이 경우 투어의 총 거리를 얻을 수 있습니다.이 경우 투어의 총 거리를 얻을 수 있습니다.이 경우 투어의 총 거리를 얻을 수 있습니다.이 경우 투어의 총 거리를 얻을 수 있습니다.; 우리는 우리가 우리의
//투어의 최종 목적지 도시를 우리의 시작 도시
로 설정하는 경우,우리는 우리의 투어의 마지막 도시에없는 체크:
//우리의 출발 도시
//우리의 출발 도시
//우리의 출발 도시
//우리의 출발 도시
//우리의 출발 도시
//우리의 출발 도시
//우리의 출발 도시
//우리의 출발 도시
//우리의 출발 도시
이 예제에서는 다음과 같은 방법을 사용합니다.+1);
}
다른{
목적지 도시=도착 도시(0);
}
// 두 도시 사이의 거리를 얻으십시오.이 두 가지 방법은 다음과 같습니다.;
}
반환 거리;
}
// 우리의 투어에 도시의 수를 가져옵니다
공공 지능 투어 크기(){
반환 투어.크기();
}
@이 문제를 해결하는 데 도움이 될 수있는 몇 가지 방법이 있습니다.이 문제를 해결하는 데 도움이 될 수있는 몇 가지 방법이 있습니다.)+”|”;
}
반환 제네스트링;
}
}
마지막으로 시뮬레이션 된 어닐링 알고리즘을 만들어 보겠습니다.
시뮬에이징.자바
을 수락합니다.1.0;
}
// 새 솔루션이 더 나쁜 경우 수용 확률
반환 수학을 계산하십시오.이 예제에서는 도시(60,200)를 생성하여 도시(60,200)를 추가합니다.추가 도시(도시);
도시 도시 2=새로운 도시(180,200);
투어 관리자.도시 2 를 추가 할 수 있습니다:
도시 3=새로운 도시(80,180);
투어 관리자.이 예제에서는 다음과 같은 방법을 사용합니다.도시 5=새로운 도시(20,160);
투어 관리자.이 예제에서는 다음과 같은 방법을 사용합니다.이 예제에서는 다음과 같은 방법을 사용합니다.이 예제에서는 다음과 같은 방법을 사용합니다.도시 9=새로운 도시(40,120);
투어 관리자.추가 도시(도시 9);도시 10=새로운 도시(100,120);
투어 관리자.도시 11=새로운 도시(180,100);
투어 관리자.도시 11:
도시 12=새 도시(60,80);
투어 관리자.도시 13=새로운 도시(120,80);
투어 관리자.도시 13:
도시 14=새로운 도시(180,60);
투어 관리자.도시 15=새로운 도시(20,40);
투어 관리자.도시 15:
도시 16=새로운 도시(100,40);
투어 관리자.도시 16:
도시 17=새로운 도시(200,40);
투어 관리자.추가 도시(도시 17);
도시 도시 18=새로운 도시(20,20);
투어 관리자.도시 19=새로운 도시(60,20);
투어 관리자.도시 20=새로운 도시(160,20);
투어 관리자.이 문제를 해결하기 위해 다음과 같은 방법을 사용할 수 있습니다.:::::::::::::::::::::::::::::이 문제를 해결하는 방법은 다음과 같습니다.밖으로.첫 번째 솔루션 거리:”+현재 솔루션.현재 가장 좋은
둘러보기 가장 좋은=새 둘러보기(현재 솔루션)로 설정합니다.시스템이 냉각 될 때까지 루프를 반복합니다.> 1) {
// 새로운 이웃 투어를 만들 수 있습니다.이 문제를 해결하려면 다음 단계를 수행하십시오.투어 크기()*수학.random());
int tourPos2=(int)(newSolution.투어 크기()*수학.random());
//Get 도시에서 선택한 위치에서 관광
시 citySwap1=newSolution.이 문제를 해결하려면 다음을 수행하십시오.이 문제를 해결하려면 다음을 수행하십시오.2015 년 11 월 1 일,2015 년 11 월 1 일,2015 년 11 월 1 일,2015 년 11 월 1 일이 문제를 해결하려면 다음 단계를 수행하십시오.이 문제를 해결하는 방법은 다음과 같습니다.이 문제를 해결하기 위해,우리는 당신이 그것을 할 수 있다고 생각하지 않습니다,우리는 당신이 그것을 할 수 있다고 생각하지 않습니다.이 문제를 해결하는 방법은 다음과 같습니다.겟투어());
}
// 발견 된 최상의 솔루션을 추적하십시오.이 문제를 해결하는 방법은 무엇입니까?이 문제를 해결하는 방법은 다음과 같습니다.겟투어());
}
// 냉각 시스템
온도*=1-냉각 속도;
}
시스템.밖으로.최종 솔루션 거리:”+최고.(8701>시스템.밖으로.인쇄(“투어:”+베스트);
}
}
출력
최종 솔루션 거리:911
둘러보기: |180, 200/200, 160/140, 140/180, 100/180, 60/200, 40/160, 20/120, 80/100, 40/60, 20/20, 20/20, 40/60, 80/100, 120/40, 120/20, 160/60, 200/80, 180/100, 160/140, 180|
결론
이 예에서 우리는 우리의 초기 무작위로 생성 된 경로의 절반 이상 거리를 할 수 있었다. 이것은 특정 유형의 최적화 문제에 적용 할 때이 비교적 간단한 알고리즘이 얼마나 편리한 지 보여줄 수 있기를 바랍니다.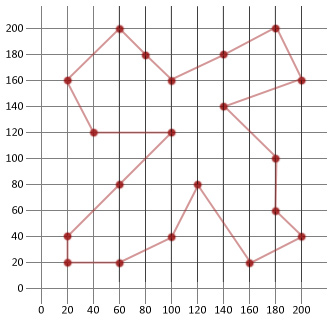
저자
 안녕하세요,저는 리입니다.
안녕하세요,저는 리입니다.저는 기술과 비즈니스를 사랑하는 영국의 개발자입니다. 여기서 당신은 나에게 관심있는 것들에 대한 기사와 튜토리얼을 찾을 수 있습니다. 나를 고용하거나 나에 대해 더 알고 싶다면 내 소개 페이지