SSIM ble først introdusert i 2004 Ieee-papiret, Image Quality Assessment: Fra Feilsynlighet til Strukturell Likhet. Abstrakt gir en god intuisjon i ideen bak systemet foreslått,
Objektive metoder for å vurdere perseptuell bildekvalitet tradisjonelt forsøkt å kvantifisere synligheten av feil (forskjeller) mellom et forvrengt bilde og et referansebilde ved hjelp av en rekke kjente egenskaper av det menneskelige visuelle systemet. Under forutsetning av at menneskelig visuell oppfatning er svært tilpasset for å trekke ut strukturell informasjon fra en scene, introduserer vi et alternativt komplementært rammeverk for kvalitetsvurdering basert på nedbrytning av strukturell informasjon.
Sammendrag: forfatterne gjør 2 viktige poeng,
- De Fleste Bildekvalitetsvurderingsteknikker er avhengige av å kvantifisere feil mellom en referanse og et eksempelbilde. En vanlig beregning er å kvantifisere forskjellen i verdiene for hver av de tilsvarende pikslene mellom prøven og referansebildene (Ved å bruke For eksempel Gjennomsnittlig Kvadrert Feil).
- Det menneskelige visuelle oppfatningssystemet er svært i stand til å identifisere strukturell informasjon fra en scene og dermed identifisere forskjellene mellom informasjonen hentet fra en referanse og en prøvescene. Derfor vil en beregning som replikerer denne virkemåten, fungere bedre på oppgaver som innebærer å skille mellom et utvalg og et referansebilde.
Den Strukturelle Likhetsindeksen (Ssim) trekker ut 3 viktige funksjoner fra et bilde:
- Luminans
- Kontrast
- Struktur
sammenligningen mellom de to bildene utføres på grunnlag av disse 3 funksjonene.
Fig 1 nedenfor viser arrangement og flyt Av Det Strukturelle Likhetsmålingssystemet. Signal X og Signal Y refererer Til Referanse-Og Eksempelbilder.

Men hva beregner denne metriske?
dette systemet beregner Den Strukturelle Likhetsindeksen mellom 2 gitte bilder som er en verdi mellom -1 og + 1. En verdi på + 1 indikerer at de 2 gitte bildene er svært like eller de samme, mens en verdi på -1 indikerer at de 2 gitte bildene er svært forskjellige. Ofte justeres disse verdiene for å være i området, hvor ekstremer har samme betydning.
la oss nå utforske kort hvordan disse funksjonene er representert matematisk, og hvordan de bidrar til den endelige ssim-poengsummen.
- Luminans: Luminans måles ved gjennomsnitt over alle pikselverdiene. Den er merket med μ (Mu) og formelen er gitt nedenfor,
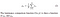
- Kontrast: Det måles ved å ta standardavviket (kvadratroten av varians) av alle pikselverdiene. Det er betegnet av σ (sigma) og representert ved formelen nedenfor,
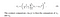
- Struktur: Den strukturelle sammenligningen gjøres ved å bruke en konsolidert formel (mer om det senere), men i hovedsak deler vi inngangssignalet med standardavviket slik at resultatet har enhetsstandardavvik som gir en mer robust sammenligning.
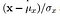
så nå har vi etablert den matematiske intuisjonen bak de tre parametrene. Men hold fast! Vi er ennå ikke ferdig med matte, litt mer. Det vi mangler nå, er sammenligningsfunksjoner som kan sammenligne de to gitte bildene på disse parametrene, og til slutt en kombinasjonsfunksjon som kombinerer dem alle. Her definerer vi sammenligningsfunksjonene og til slutt kombinasjonsfunksjonen som gir likhetsindeksverdien
- luminans sammenligningsfunksjon: den er definert av en funksjon, l (x, y)som er vist nedenfor. μ (mu) representerer gjennomsnittet av et gitt bilde. x og y er de to bildene som blir sammenlignet.
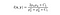
Hvor C1 er en konstant for å sikre stabilitet når nevneren blir 0. C1 er gitt ved,
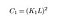
Update: Gjennom hele artikkelen hadde vi ikke utforsket Hva K-og L-konstantene i denne ligningen er. Heldigvis pekte en leser det ut i kommentarene, og så for å gjøre denne artikkelen litt mer nyttig, vil jeg bare definere dem her.
L er det dynamiske området for pikselverdier (vi setter det som 255 siden vi har å gjøre med standard 8-biters bilder). Du kan lese mer om hva som er de forskjellige bildetypene og hva de betyr, her.
K1, K2 er bare normale konstanter, ikke mye der!
- Kontrast sammenligningsfunksjon: den er definert av en funksjon c(x, y) som er vist nedenfor. σ betegner standardavviket for et gitt bilde. x og y er de to bildene som blir sammenlignet.
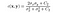
Hvor C2 er gitt ved,
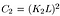
- Struktur sammenligning funksjon: det er definert av funksjonen s (x, y) som er vist nedenfor. σ betegner standardavviket for et gitt bilde. x og y er de to bildene som blir sammenlignet.
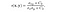
hvor σ (xy) er definert som,
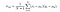
OG TIL slutt er SSIM-poengsummen gitt av,

der α > 0, β > 0, γ > 0 betegner den relative betydningen av hver av beregningene. For å forenkle uttrykket, hvis vi antar, α = β = 1 og C3 = C2/2, kan vi få,
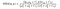
Men det er en vri!
mens DU vil kunne implementere SSIM ved hjelp av de ovennevnte formlene, er det sjansen for at det ikke vil være så godt som de klare implementeringene som er tilgjengelige, som forfatterne forklarer det,
for bildekvalitetsvurdering er det nyttig å bruke ssim-indeksen lokalt i stedet for globalt. Først, bilde statistiske funksjoner er vanligvis svært romlig nonstationary. For det andre kan bildeforvrengninger, som kan eller ikke kan avhenge av den lokale bildestatistikken, også være romvariant. For det tredje, ved typiske visningsavstander, kan bare et lokalt område i bildet oppfattes med høy oppløsning av den menneskelige observatøren på en gang (på grunn AV foveation-funksjonen TIL HVS ). Og til slutt kan lokalisert kvalitetsmåling gi et romlig varierende kvalitetskart over bildet, som gir mer informasjon om kvalitetsforringelsen av bildet og kan være nyttig i enkelte applikasjoner.
Sammendrag: I stedet for å bruke de ovennevnte beregningene globalt (dvs. over hele bildet samtidig), er det bedre å bruke beregningene regionalt(dvs. i små deler av bildet og ta gjennomsnittet generelt).
denne metoden blir ofte referert Til Som Den Gjennomsnittlige Strukturelle Likhetsindeksen.
på grunn av denne endringen i tilnærmingen fortjener våre formler også endringer for å gjenspeile det samme (det bør bemerkes at denne tilnærmingen er mer vanlig og vil bli brukt til å forklare koden).
(Merk: hvis innholdet nedenfor virker litt overveldende, ingen bekymringer! Hvis du får tak i det, vil det å gå gjennom koden gi deg en mye klarere ide.)
forfatterne bruker en 11×11 sirkulær-symmetrisk Gaussisk Veiefunksjon (i utgangspunktet en 11×11 matrise hvis verdier er avledet fra en gaussisk fordeling) som beveger piksel for piksel over hele bildet. Ved hvert trinn beregnes den lokale statistikken og ssim-indeksen i det lokale vinduet. Siden vi nå beregner beregningene lokalt, blir våre formler revidert som,
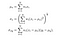
hvor wi er den gaussiske vektingsfunksjonen.
hvis du fant dette litt unintuitive, ingen bekymringer! Det er nok å forestille seg wi som en multiplikasjonog som brukes til å beregne de nødvendige verdiene ved hjelp av noen matematiske triks.
Når beregninger er utført over hele bildet, tar vi bare gjennomsnittet av alle de lokale ssim-verdiene og kommer til den globale ssim-verdien.
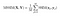
endelig ferdig med teorien! Nå over til koden!