Lær OpenCV

I dette innlegget vil vi lære detaljene I Histogrammet Av Orienterte Gradienter (HOG) feature descriptor. Vi vil lære hva som er under hetten og hvordan denne beskrivelsen beregnes internt Av OpenCV, MATLAB og andre pakker.

dette innlegget er en del av en serie jeg skriver Om Bildegjenkjenning og Objektdeteksjon.

den komplette listen over tutorials i denne serien er gitt nedenfor:

1. Bildegjenkjenning ved hjelp av tradisjonelle Datasynteknikker : Del 1
2. Histogram Av Orienterte Gradienter : Del 2
3. Eksempelkode for bildegjenkjenning : Del 3
4. Trening av en bedre øyedetektor: Del 4a
5. objektdeteksjon ved hjelp av tradisjonelle Datasynteknikker : Del 4b
6. hvordan trene og teste Din Egen OpenCV-objektdetektor : Del 5
7. bildegjenkjenning ved hjelp av dyp læring : Del 6
   • Introduksjon Til Nevrale Nettverk
   • Forstå Feedforward Nevrale Nettverk
   • Bildegjenkjenning ved Hjelp Av Convolutional Nevrale Nettverk
8. Objektdeteksjon ved Hjelp Av Dyp Læring: Del 7

Mange ting ser vanskelig og mystisk ut. Men når du tar deg tid til å dekonstruere dem, er mysteriet erstattet av mestring, og det er det vi er ute etter. Hvis Du er nybegynner og finner Datasyn hardt og mystisk, husk bare følgende

Spørsmål : Hvordan spiser du en elefant ?
A : En bit om gangen!

Hva er En Funksjonsbeskrivelse?

en funksjonsbeskrivelse er en representasjon av et bilde eller en bildepatch som forenkler bildet ved å trekke ut nyttig informasjon og kaste bort overflødig informasjon.

vanligvis konverterer en funksjonsbeskrivelse et bilde av størrelse bredde x høyde x 3 (kanaler ) til en funksjonsvektor / matrise av lengde n. I TILFELLE AV HOG-funksjonsbeskrivelsen er inngangsbildet av størrelse 64 x 128 x 3 og utgangsfunksjonsvektoren er av lengde 3780.

Husk AT HOG descriptor kan beregnes for andre størrelser, men i dette innlegget stikker jeg til tall som presenteres i originalpapiret, slik at du lett kan forstå konseptet med et konkret eksempel.

alt dette høres bra ut, men hva er «nyttig» og hva er «overflødig» ? For å definere «nyttig», må vi vite hva er det «nyttig» for ? Det er klart at funksjonsvektoren ikke er nyttig for å vise bildet. Men det er veldig nyttig for oppgaver som bildegjenkjenning og objektdeteksjon. Funksjonen vektor produsert av disse algoritmene når matet inn i et bilde klassifisering algoritmer som Support Vector Machine (SVM) gir gode resultater.

men hvilke typer «funksjoner» er nyttige for klassifiseringsoppgaver ? La oss diskutere dette punktet ved hjelp av et eksempel. Anta at vi vil bygge en objektdetektor som oppdager knapper på skjorter og strøk.

en knapp er sirkulær ( kan se elliptisk ut i et bilde ) og har vanligvis noen hull for sying. Du kan kjøre en kantdetektor på bildet av en knapp, og enkelt fortelle om det er en knapp ved å bare se på kantbildet alene. I dette tilfellet er kantinformasjon «nyttig» og fargeinformasjon er ikke. I tillegg må funksjonene også ha diskriminerende kraft. For eksempel bør gode funksjoner hentet fra et bilde kunne fortelle forskjellen mellom knapper og andre sirkulære objekter som mynter og bildekk.

i HOG feature descriptor brukes fordelingen ( histogrammer ) av retninger av gradienter ( orienterte gradienter ) som funksjoner. Gradienter (x-og y-derivater) av et bilde er nyttige fordi størrelsen på gradienter er stor rundt kanter og hjørner ( områder med brå intensitetsendringer), og vi vet at kanter og hjørner pakker inn mye mer informasjon om objektform enn flate områder.

hvordan beregne Histogram Av Orienterte Gradienter ?

i denne delen vil vi gå inn i detaljene for beregning AV HOG feature descriptor. For å illustrere hvert trinn, vil vi bruke en oppdatering av et bilde.

Trinn 1 : Forbehandling

SOM nevnt tidligere ER HOG feature descriptor brukt til fotgjengerregistrering beregnet på en 64×128 oppdatering av et bilde. Selvfølgelig kan et bilde være av hvilken som helst størrelse. Vanligvis patcher på flere skalaer er analysert på mange bilde steder. Den eneste begrensningen er at patchene som analyseres, har et fast aspektforhold. I vårt tilfelle må patchene ha et aspektforhold på 1: 2. For eksempel kan det være 100×200, 128 hryvnias 256 eller 1000 hryvnias 2000 men ikke 101 hryvnias 205.

for å illustrere dette punktet har jeg vist et stort bilde av størrelse 720×475. Vi har valgt en oppdatering av størrelse 100×200 for å beregne VÅR HOG feature descriptor. Denne oppdateringen er beskåret ut av et bilde og endret til 64×128. Nå er vi klare til å beregne HOG descriptor for dette bildet patch.

papiret Fra Dalal og Triggs nevner også gammakorreksjon som et preprocessing-trinn, men ytelsesgevinstene er små, og så hopper vi over trinnet.

Trinn 2: Beregn Gradientbildene

for å beregne EN HOG descriptor må vi først beregne horisontale og vertikale gradienter; tross alt vil vi beregne histogrammet av gradienter. Dette oppnås lett ved å filtrere bildet med følgende kjerner.

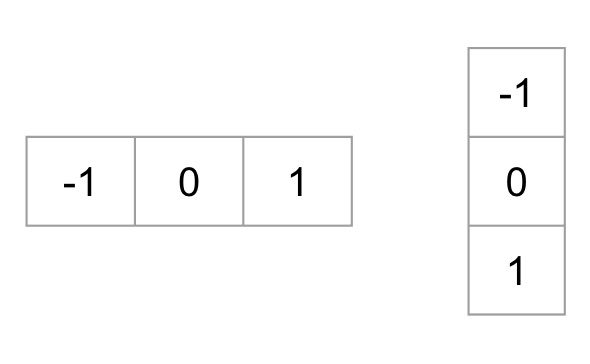
Vi kan også oppnå de samme resultatene, ved å bruke Sobel operatør I OpenCV med kjernestørrelse 1.

// C++ gradient calculation.// Read imageMat img = imread("bolt.png");img.convertTo(img, CV_32F, 1/255.0);// Calculate gradients gx, gyMat gx, gy;Sobel(img, gx, CV_32F, 1, 0, 1);Sobel(img, gy, CV_32F, 0, 1, 1);

# Python gradient calculation # Read imageim = cv2.imread('bolt.png')im = np.float32(im) / 255.0# Calculate gradientgx = cv2.Sobel(img, cv2.CV_32F, 1, 0, ksize=1)gy = cv2.Sobel(img, cv2.CV_32F, 0, 1, ksize=1)

Deretter kan vi finne størrelsen og retningen av gradienten ved hjelp av følgende formel

hvis Du bruker OpenCV, kan beregningen gjøres ved hjelp av funksjonen cartToPolar som vist nedenfor.

// C++ Calculate gradient magnitude and direction (in degrees)Mat mag, angle;cartToPolar(gx, gy, mag, angle, 1);

Den samme koden i python ser slik ut.

# Python Calculate gradient magnitude and direction ( in degrees )mag, angle = cv2.cartToPolar(gx, gy, angleInDegrees=True)

figuren nedenfor viser gradientene.

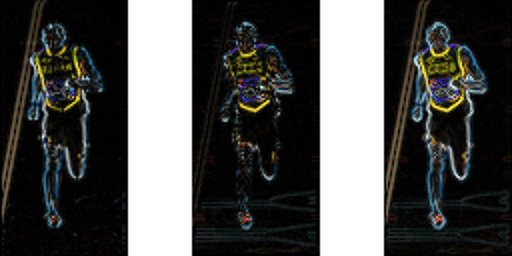
Legg Merke til at x-gradienten fyrer av på vertikale linjer og y-gradienten fyrer av på horisontale linjer. Omfanget av gradient branner der noen gang det er en skarp endring i intensitet. Ingen av dem brann når regionen er glatt. Jeg har bevisst utelatt bildet som viser retningen av gradient fordi retning vist som et bilde ikke formidler mye.

gradientbildet fjernet mye ikke-essensiell informasjon (f. eks. konstant farget bakgrunn ), men uthevede konturer. Med andre ord kan du se på gradientbildet og fortsatt enkelt si at det er en person i bildet.

ved hver piksel har gradienten en størrelsesklasse og en retning. For fargebilder evalueres gradientene til de tre kanalene (som vist i figuren ovenfor ). Gradientstørrelsen på en piksel er maksimum av gradientstørrelsen på de tre kanalene, og vinkelen er vinkelen som svarer til maksimal gradient.

Trinn 3: Beregn Histogram Av Graderinger i 8×8 celler

i dette trinnet er bildet delt inn i 8×8 celler og et histogram av gradienter beregnes for hver 8×8 celler.

vi vil lære om histogrammer om et øyeblikk, men før vi går dit, la oss først forstå hvorfor vi har delt bildet i 8×8 celler. En av de viktigste grunnene til å bruke en funksjonsbeskrivelse for å beskrive en oppdatering av et bilde er at den gir en kompakt representasjon. En 8×8 bildeplaster inneholder 8x8x3 = 192 pikselverdier. Gradienten av denne oppdateringen inneholder 2 verdier (størrelse og retning ) per piksel som legger opp til 8x8x2 = 128 tall.

ved slutten av denne delen vil vi se hvordan disse 128 tallene er representert ved hjelp av en 9-bin histogram som kan lagres som en matrise av 9 tall. Ikke bare er representasjonen mer kompakt, beregning av et histogram over en patch gjør denne representasjonen mer robust for støy. Individuelle gradenter kan ha støy, men et histogram over 8×8 patch gjør representasjonen mye mindre følsom for støy.

men hvorfor 8×8 patch ? Hvorfor ikke 32×32 ? Det er et designvalg informert av omfanget av funksjoner vi leter etter. HOG ble brukt til fotgjenger deteksjon i utgangspunktet. 8×8 celler i et bilde av en fotgjenger skalert til 64×128 er store nok til å fange interessante funksjoner(f. eks ansiktet, toppen av hodet etc. ).

histogrammet er i hovedsak en vektor (eller en matrise ) av 9 hyller (tall ) som svarer til vinkler 0, 20, 40, 60 … 160.

La oss se på en 8×8 patch i bildet og se hvordan gradientene ser ut.

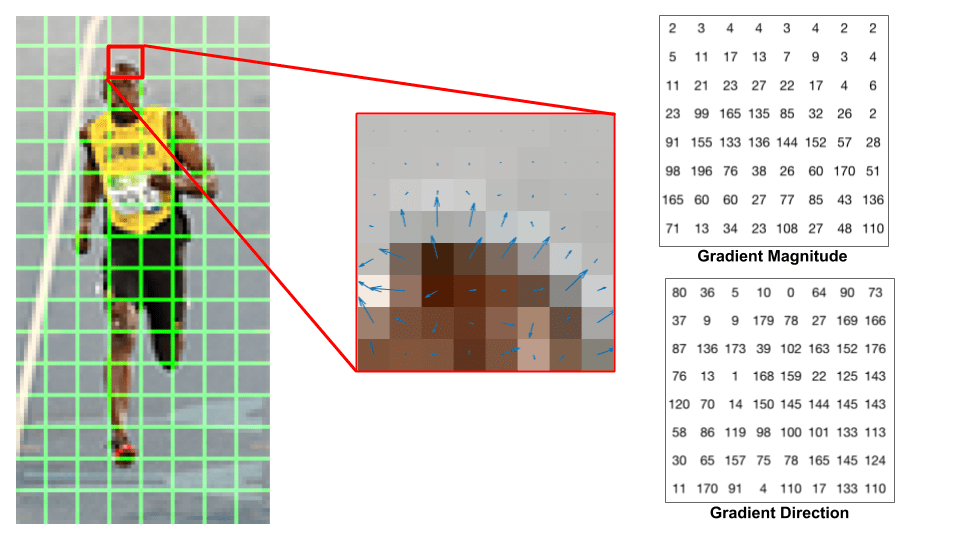
Hvis du er nybegynner i datasyn, er bildet i midten veldig informativt. Det viser oppdateringen av bildet overlaid med piler som viser gradienten-pilen viser retningen av gradienten og lengden viser størrelsen. Legg merke til hvordan pilens retning peker på retningen for endring i intensitet og størrelsen viser hvor stor forskjellen er.

til høyre ser vi rattallene som representerer gradientene i de 8×8 cellene med en mindre forskjell-vinklene er mellom 0 og 180 grader i stedet for 0 til 360 grader. Disse kalles» usignerte » gradienter fordi en gradient og den negative er representert av de samme tallene. Med andre ord, en gradientpil og den ene 180 grader motsatt den regnes som den samme. Men hvorfor ikke bruke 0 – 360 grader ?

Empirisk har det vist seg at usignerte gradienter fungerer bedre enn signerte gradienter for fotgjenger deteksjon. Noen implementeringer AV HOG vil tillate deg å angi om du vil bruke signerte gradienter.

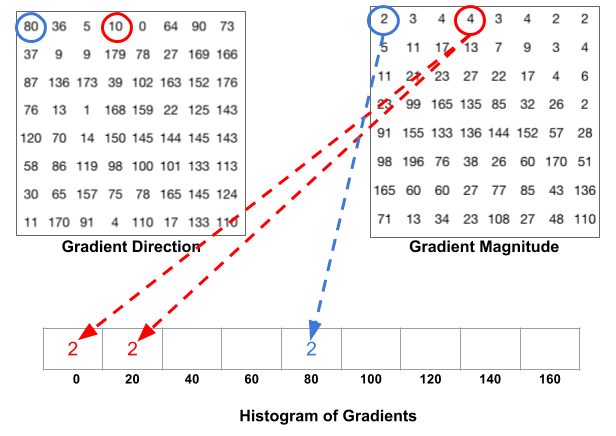
neste trinn er å lage et histogram av gradienter i disse 8×8 cellene. Histogrammet inneholder 9 hyller som tilsvarer vinkler 0, 20, 40 … 160. Følgende figur illustrerer prosessen. Vi ser på størrelsen og retningen av gradienten til den samme 8×8 patch som i forrige figur.

en hylle velges basert på retningen, og avstemningen (verdien som går inn i hyllen ) velges basert på størrelsen. La oss først fokusere på pikselen omkranset i blått. Den har en vinkel (retning ) på 80 grader og størrelsen på 2. Så det legger 2 til 5th bin. Gradienten ved piksel omkranset ved hjelp av rødt har en vinkel på 10 grader og størrelsen på 4. Siden 10 grader er halvveis mellom 0 og 20, deles avstemningen av pikselen jevnt i de to hyllene.

Det er en detalj å være klar over. Hvis vinkelen er større enn 160 grader, er den mellom 160 og 180, og vi vet at vinkelen brytes rundt å gjøre 0 og 180 ekvivalent. Så i eksemplet nedenfor bidrar pikselet med vinkel 165 grader proporsjonalt til 0 graders hylle og 160 graders hylle.

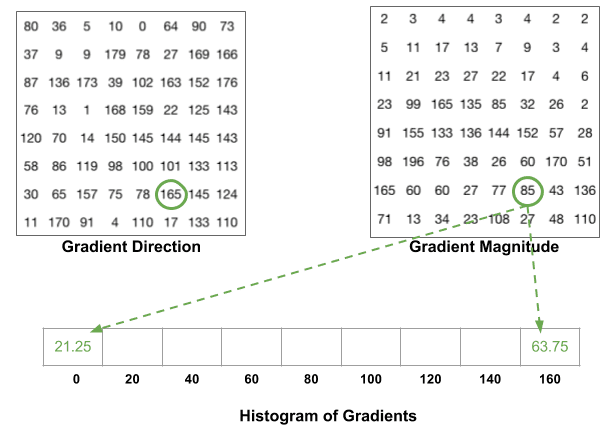
bidragene fra alle pikslene i de 8×8 cellene legges sammen for å lage 9-bin histogrammet. For lappen ovenfor ser det slik ut

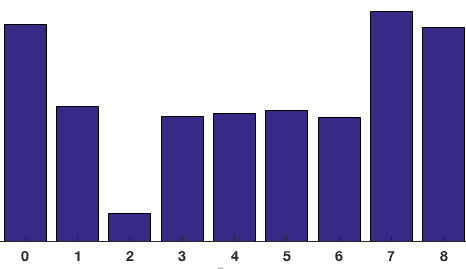
i vår representasjon er y-aksen 0 grader. Du kan se at histogrammet har mye vekt nær 0 og 180 grader, noe som bare er en annen måte å si at i patchgradientene peker enten opp eller ned.

Trinn 4 : 16×16 Blokk Normalisering

i det forrige trinnet opprettet vi et histogram basert på gradienten av bildet. Gradienter av et bilde er følsomme for generell belysning. Hvis du gjør bildet mørkere ved å dele alle pikselverdier med 2, endres gradientstørrelsen med halvparten, og derfor endres histogramverdiene med halvparten.

Ideelt sett ønsker vi at vår deskriptor skal være uavhengig av belysningsvariasjoner. Med andre ord ønsker vi å «normalisere» histogrammet slik at de ikke påvirkes av lysvariasjoner.

Før jeg forklarer hvordan histogrammet er normalisert, la oss se hvordan en vektor med lengde 3 er normalisert.

La oss si at VI har EN rgb-fargevektor . Lengden på denne vektoren er $\sqrt{128^2 + 64^2 + 32^2} = 146.64$. Dette kalles også l2-normen til vektoren. Å dele hvert element av denne vektoren med 146,64 gir oss en normalisert vektor .

vurder nå en annen vektor der elementene er to ganger verdien av den første vektoren 2 x = . Du kan finne ut av det selv for å se at normalisering vil resultere i, som er den samme som den normaliserte versjonen av den opprinnelige rgb-vektoren. Du kan se at normalisering av en vektor fjerner skalaen.

Nå som vi vet hvordan vi skal normalisere en vektor, kan du bli fristet til å tro at mens du beregner HOG, kan du bare normalisere 9×1 histogrammet på samme måte som vi normaliserte 3×1 vektoren ovenfor. Det er ikke en dårlig ide, men en bedre ide er å normalisere over en større blokk med 16×16.

En 16×16 blokk har 4 histogrammer som kan sammenkobles for å danne en 36 x 1 elementvektor, og den kan normaliseres akkurat slik en 3×1 vektor normaliseres. Vinduet flyttes deretter med 8 piksler (se animasjon) og en normalisert 36×1 vektor beregnes over dette vinduet og prosessen gjentas.

Trinn 5: Beregn HOG feature vector

for å beregne den endelige feature vector for hele bildet patch, de 36×1 vektorer er satt sammen til en gigantisk vektor. Hva er størrelsen på denne vektoren ? La oss beregne

1. Hvor mange posisjoner av de 16×16 blokkene har vi ? Det er 7 horisontale og 15 vertikale stillinger som gir totalt 7 x 15 = 105 stillinger.
2. hver 16×16 blokk er representert ved en 36×1 vektor. Så når vi sammenkobler dem alle til en gaint-vektor, får vi en 36×105 = 3780 dimensjonsvektor.

Visualisere Histogram Av Orienterte Gradienter

HOGBESKRIVELSEN til en bildepatch er vanligvis visualisert ved å plotte de 9×1 normaliserte histogrammene i de 8×8 cellene. Se bildet på siden. Du vil legge merke til at dominerende retning av histogrammet fanger formen på personen, spesielt rundt torso og ben.

Dessverre er Det Ingen enkel måte å visualisere HOG descriptor I OpenCV.

Abonner & Last Ned Kode