det elektriske feltet E kan alltid uttrykkes som gradienten til en skalarpotensialfunksjon
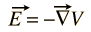
det er ikke noe generelt skalarpotensial for magnetfelt B, men det kan uttrykkes som krøllen til en vektorfunksjon
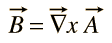
denne funksjonen a er gitt navnet «vektorpotensial», men det er ikke direkte knyttet til arbeid slik det skalarpotensialet er.
vektorpotensialet er definert til Å være i samsvar Med Amperes Lov og kan uttrykkes i form av enten nåværende i eller nåværende tetthet j (kildene til magnetfelt). I ulike tekster tar denne definisjonen skjemaene
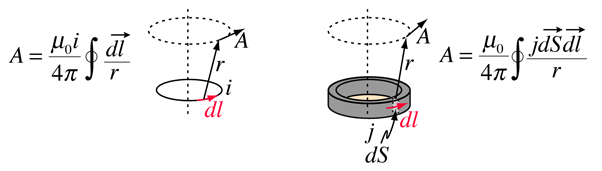
en begrunnelse for vektorpotensialet er at det kan være lettere å beregne vektorpotensialet enn å beregne magnetfeltet direkte fra en gitt kildestrømgeometri. Den vanligste applikasjonen er antenneteori og beskrivelse av elektromagnetiske bølger.
siden magnetfeltet B er definert som krøllen Til A, og ved vektoridentiteten er krøllen til en gradient identisk null, kan enhver vilkårlig funksjon som kan uttrykkes som gradienten til en skalarfunksjon legges til A uten å endre verdien Av B oppnådd fra Den. Det vil Si, A ‘kan fritt erstattes av en hvor
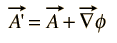
Slike transformasjoner kalles måle transformasjoner, og det har vært en rekke «målere» som har blitt brukt til fordel er bestemte typer beregninger i elektromagnetisk teori.