Å Finne en optimal løsning for visse optimaliseringsproblemer kan være en utrolig vanskelig oppgave, ofte praktisk talt umulig. Dette skyldes at når et problem blir tilstrekkelig stort, må vi søke gjennom et enormt antall mulige løsninger for å finne den optimale. Selv med moderne datakraft er det fortsatt ofte for mange mulige løsninger å vurdere. I dette tilfellet fordi vi ikke realistisk kan forvente å finne den optimale innen en fornuftig tid, må vi betale for noe som er nært nok.
et eksempel optimalisering problem som vanligvis har et stort antall mulige løsninger ville være den reiser selger problem. For å finne en løsning på et problem som reiser selger problemet må vi bruke en algoritme som er i stand til å finne en god nok løsning i en rimelig tid. I en tidligere veiledning så vi på hvordan vi kunne gjøre dette med genetiske algoritmer, og selv om genetiske algoritmer er en måte vi kan finne en ‘god nok’ løsning på reiseselgerproblemet, er det andre enklere algoritmer vi kan implementere som også vil finne oss en nær optimal løsning. I denne opplæringen algoritmen vi skal bruke er, ‘simulert annealing’.
hvis du ikke er kjent med traveling salesman-problemet, kan det være verdt å ta en titt på min tidligere opplæring før du fortsetter.
Hva Er Simulert Annealing?
Først, la Oss se på hvordan simulert annealing fungerer, og hvorfor det er bra å finne løsninger på reiseselgerproblemet spesielt. Den simulerte glødealgoritmen ble opprinnelig inspirert fra prosessen med glødning i metallarbeid. Annealing innebærer oppvarming og kjøling av et materiale for å endre dets fysiske egenskaper på grunn av endringene i sin indre struktur. Som metallet kjøler sin nye struktur blir fast, følgelig forårsaker metallet til å beholde sine nylig oppnådd egenskaper. I simulert annealing holder vi en temperaturvariabel for å simulere denne oppvarmingsprosessen. Vi først satt det høyt og deretter la det sakte ‘kult’ som algoritmen kjører. Selv om denne temperaturvariabelen er høy, vil algoritmen bli tillatt, med mer frekvens, å akseptere løsninger som er verre enn vår nåværende løsning. Dette gir algoritmen muligheten til å hoppe ut av noen lokale optimums det befinner seg tidlig i utførelsen. Når temperaturen er redusert, er sjansen for å akseptere verre løsninger, slik at algoritmen gradvis kan fokusere på et område av søkeplassen der forhåpentligvis en nær optimal løsning kan bli funnet. Denne gradvise ‘kjøling’ prosessen er det som gjør simulert annealing algoritmen bemerkelsesverdig effektiv på å finne en nær optimal løsning når du arbeider med store problemer som inneholder mange lokale optimums. Naturen av reiser selger problemet gjør det til et perfekt eksempel.
Fordeler Med Simulert Annealing
du lurer kanskje på om Det er noen reell fordel å implementere simulert annealing over noe som en enkel bakkeklatrer. Selv om hill klatrere kan være overraskende effektiv på å finne en god løsning, de har også en tendens til å sette seg fast i lokale optimums. Som vi tidligere har bestemt, er den simulerte glødealgoritmen utmerket for å unngå dette problemet og er mye bedre i gjennomsnitt på å finne et omtrentlig globalt optimum.
for å få bedre forståelse, la oss raskt se på hvorfor en grunnleggende bakkeklatringsalgoritme er så tilbøyelig til å bli fanget i lokale optimum.
en bakkeklatreralgoritme vil ganske enkelt akseptere naboløsninger som er bedre enn dagens løsning. Når klatreren ikke finner noen bedre naboer, stopper den.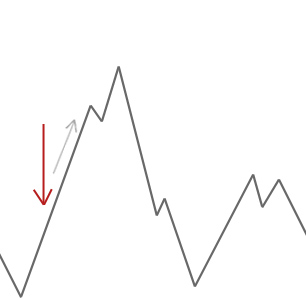
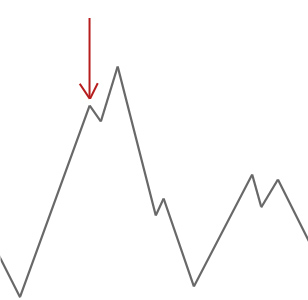
i eksemplet ovenfor starter vi vår bakkeklatrer ved den røde pilen, og den jobber seg oppover bakken til den når et punkt der den ikke kan klatre noe høyere uten først å synke. I dette eksemplet kan vi tydelig se at det sitter fast i et lokalt optimum. Hvis dette var et ekte verdensproblem, ville vi ikke vite hvordan søkeplassen ser ut, så dessverre ville vi ikke kunne fortelle om denne løsningen er hvor som helst nær et globalt optimum.
Simulert glødning virker litt annerledes enn dette og vil av og til akseptere verre løsninger. Denne egenskapen ved simulert glødning hjelper det å hoppe ut av eventuelle lokale optimums det ellers kunne ha sittende fast i.
Akseptfunksjon
La oss ta en titt på hvordan algoritmen bestemmer hvilke løsninger som skal aksepteres, slik at vi bedre kan forstå hvordan det er i stand til å unngå disse lokale optimumene.
først sjekker vi om naboløsningen er bedre enn vår nåværende løsning. Hvis det er, aksepterer vi det betingelsesløst. Hvis imidlertid nabo-løsningen ikke er bedre, må vi vurdere et par faktorer. For det første, hvor mye verre nabo løsningen er; og for det andre, hvor høy dagens ‘temperatur’ av vårt system er. Ved høye temperaturer systemet er mer sannsynlig akseptere løsninger som er verre.
matematikken for dette er ganske enkel:
I Utgangspunktet er jo mindre endringen i energi (løsningens kvalitet), og jo høyere temperaturen er, desto mer sannsynlig er det for algoritmen å akseptere løsningen.
Algoritmeoversikt
Så hvordan ser algoritmen ut? Vel, i sin mest grunnleggende implementering er det ganske enkelt.
- først må vi sette starttemperaturen og lage en tilfeldig innledende løsning.
- så begynner vi looping til vår stopptilstand er oppfylt. Vanligvis har systemet enten tilstrekkelig avkjølt, eller det er funnet en god nok løsning.
- Herfra velger vi en nabo ved å gjøre en liten endring i vår nåværende løsning.
- vi bestemmer da om vi skal flytte til naboløsningen.
- til Slutt senker vi temperaturen og fortsetter looping
Temperaturinitialisering
For bedre optimalisering, bør vi ved initialisering av temperaturvariabelen velge en temperatur som i utgangspunktet tillater praktisk talt enhver bevegelse mot den nåværende løsningen. Dette gir algoritmen muligheten til å bedre utforske hele søkeområdet før kjøling og bosetting i en mer fokusert region.
Eksempelkode
la Oss nå bruke det vi vet for å lage en grunnleggende simulert annealingalgoritme, og bruk den deretter på traveling salesman-problemet nedenfor. Vi skal bruke Java i denne opplæringen, men logikken skal forhåpentligvis være enkel nok til å kopiere til et hvilket som helst språk du ønsker.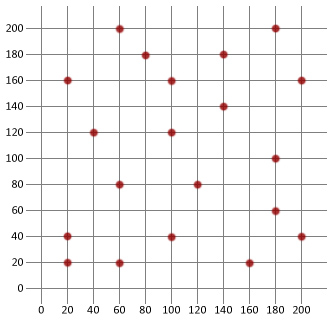
Først må vi opprette En by klasse som kan brukes til å modellere de ulike destinasjonene av våre reiser selger.
Byen.java
* By.java
* Modeller en by
* /
pakke sa;
offentlig klasse by {
int x;
int y;
/ / Konstruerer en tilfeldig plassert by
offentlig By () {
dette.x = (int) (Matematikk.tilfeldig ()*200);
dette.y = (int) (Matematikk.tilfeldig()*200);
}
// Konstruerer en by på valgt x, y sted
offentlig By (int x, int y) {
dette.x = x;
dette.y = y;
}
// Får byens x-koordinat
offentlig int getX () {
returner dette.x;
}
// Får byens y-koordinat
offentlig int getY () {
returner dette.y;
}
// Får avstanden til gitt by
offentlig dobbel distanceTo (By by) {
int xDistance = Matte.abs (getX () – by.getX());
int yDistance = Matematikk.abs (getY () – byen.getY ());
dobbel avstand = Matte.sqrt ((xDistance*xDistance) + (yDistance*yDistance) );
returavstand;
}
@Overstyr
offentlig Streng toString () {
retur getX ()+», » + getY();
}
}
Neste la oss lage en klasse som kan holde styr på byene.
TourManager.java
* TourManager.java
* Holder byene i en tur
* /
pakke sa;
importer java.util.ArrayList;
public class TourManager {
/ / Holder våre byer
privat statisk ArrayList destinationCities = ny ArrayList< By>();
// Legger til en destinasjonsby
offentlig statisk ugyldig addCity (Byby) {
destinationCities.legg til (by);
}
// Få en by
offentlig statisk by getCity (int index) {
retur (By)destinationCities.get (indeks);
}
// Få antall reisemål byer
offentlig statisk int numberOfCities () {
retur destinationCities.størrelse();
}
}
nå for å lage klassen som kan modellere en omreisende selger tur.
Tur.java
* Tur.java
* Lagrer en kandidat tur gjennom alle byer
* /
pakke sa;
import java.util.Arraylist;
importer java.util.Samlinger;
public class Tour {
/ / Holder vår tur til byer
privat ArrayList tour = ny ArrayList < By>();
// Cache
privat int avstand = 0;
/ / Konstruerer en tom tur
offentlig Tur () {
for (int i = 0; i < TourManager.numberOfCities (); i++) {
tur.legg til (null);
}
}
// Konstruerer en tur fra en annen tur
offentlig Tur (ArrayList tour) {
dette.tur = (ArrayList) tur.klone();
}
// Returnerer turinformasjon
offentlig ArrayList getTour () {
retur tur;
}
// Oppretter en tilfeldig person
offentlig ugyldig generateIndividual () {
/ / Loop gjennom alle våre reisemål byer og legge dem til vår tur
for (int cityIndex = 0; cityIndex < TourManager.numberOfCities (); cityIndex++) {
setCity(cityIndex, TourManager.getCity (cityIndex)));
}
// Tilfeldig omorganisere tour
Samlinger.shuffle (omvisning);
}
/ / Får en by fra turen
offentlig by getCity (int tourPosition) {
retur (By)tur.get (turposisjon);
}
// Angir en by i en bestemt posisjon i en tur
offentlig ugyldig setCity (int tourPosition, City city) {
tour.set (turposisjon, by);
/ / Hvis turene er endret, må vi tilbakestille treningen og avstanden
avstand = 0;
}
// Får total distanse på turen
public int getDistance () {
if (distance == 0) {
int tourDistance = 0;
/ / Loop gjennom turens byer
for (int cityIndex=0; cityIndex < tourSize(); cityIndex++) {
// Get city vi reiser fra
City fromCity = getCity(cityIndex);
// City vi reiser til
city destinationCity;
// Sjekk vi er ikke på vår tur siste by, hvis vi er satt vår
// turens endelige destinasjon by til vår startby
hvis(cityIndex+1 < turstørrelse()){
destinationcity = getcity(cityindex+1);
}
else{
destinationCity = getCity(0);
}
// Få avstanden mellom de to byene
turavstand + = fromCity.distanceTo (destinationCity);
}
avstand = turavstand;
}
returavstand;
}
// Få antall byer på vår tur
public int tourSize () {
tur / retur.størrelse();
}
@Overstyr
offentlig Streng toString () {
streng geneString=»|»;
for (int i = 0; i < tourSize (); i++) {
geneString += getCity (i)+»|»;
}
retur geneString;
}
}
Til Slutt, la oss lage vår simulerte glødealgoritme.
SimulatedAnnealing.java
offentlig klasse Simulertannealing {
// Beregn akseptsannsynligheten
offentlig statisk dobbel akseptsannsynlighet (int energi, int newenergi, dobbel temperatur) {
/ / hvis den nye løsningen er bedre, aksepter den
if (newenergi < energi) {
retur 1.0;
}
// hvis den nye løsningen er verre, beregner du en akseptsannsynlighet
return Math.exp ((energi – newEnergy) / temperatur);
}
offentlig statisk tomrom hoved (Streng args) {
// Opprett og legg til våre byer
By by = ny By(60, 200);
TourManager.addCity (by);
By city2 = ny By (180, 200);
TourManager.addCity (city2);
By city3 = ny By (80, 180);
TourManager.addCity (city3);
By city4 = ny By (140, 180);
TourManager.addCity (city4);
By city5 = ny By (20, 160);
TourManager.addCity (city5);
By city6 = ny By (100, 160);
TourManager.addCity (city6);
By city7 = ny By (200, 160);
TourManager.addCity (city7);
By city8 = ny By (140, 140);
TourManager.addCity (city8);
By city9 = ny By (40, 120);
TourManager.addCity (by9);
By city10 = ny By (100, 120);
TourManager.addCity (city10);
By city11 = ny By (180, 100);
TourManager.addCity (city11);
By city12 = ny By (60, 80);
TourManager.addCity (city12);
By city13 = ny By(120, 80);
TourManager.addCity (city13);
By city14 = ny By(180, 60);
TourManager.addCity (city14);
By city15 = ny By (20, 40);
TourManager.addCity (city15);
By city16 = ny By(100, 40);
TourManager.addCity (by16);
By17 = ny By(200, 40);
TourManager.addCity (by17);
By city18 = ny By (20, 20);
TourManager.addCity (city18);
By city19 = ny By(60, 20);
TourManager.addCity (by19);
By20 = ny By(160, 20);
TourManager.addCity (city20);
// Sett innledende temp
dobbel temp = 10000;
// Kjølehastighet
dobbel kjølehastighet = 0,003;
/ / Initialiser innledende løsning
tour currentSolution = ny Tur ();
currentSolution.generateIndividual ();
System.ut.println («Initial løsning avstand:» + currentSolution . getDistance ());
/ / Sett som dagens beste
Tour best = ny Tur (currentSolution.Gettour());
// Loop til systemet har avkjølt
mens (temp > 1) {
// Opprett ny neighbour tour
Tour newSolution = ny Tur (currentSolution.getTour ());
// Få tilfeldige stillinger i turen
int tourPos1 = (int) (newSolution.tourSize () * Matte.tilfeldig ());
int tourPos2 = (int) (newSolution.tourSize () * Matte.tilfeldig ());
// Få byene på utvalgte stillinger i turen
By citySwap1 = newSolution.getCity (tourPos1);
By citySwap2 = newSolution.getCity (tourPos2);
// Bytt dem
newSolution.setCity (tourPos2, citySwap1);
newSolution.setCity (tourPos1, citySwap2);
// Få energi av løsninger
int currentEnergy = currentSolution.getDistance ();
int neighbourEnergy = newSolution.getDistance ();
// Bestem om vi skal godta naboen
hvis (akseptanseprobability (currentEnergy, neighbourEnergy, temp)> Matte .tilfeldig ()) {
currentSolution = ny Tur (newSolution.getTour());
}
// Hold styr på den beste løsningen funnet
if (currentSolution.getDistance () < beste.getDistance ()) {
best = ny Tur (currentSolution.getTour());
}
// Kjølesystem
temp * = 1-kjølehastighet;
}
System.ut.println («Endelig løsning avstand:» + best.getDistance ());
System.ut.println («Tour:» + best);
}
}
Utgang
Endelig løsningsavstand: 911
Tur: |180, 200/200, 160/140, 140/180, 100/180, 60/200, 40/160, 20/120, 80/100, 40/60, 20/20, 20/20, 40/60, 80/100, 120/40, 120/20, 160/60, 200/80, 180/100, 160/140, 180|
Konklusjon
I dette eksemplet var vi i stand til mer enn halvparten av avstanden til vår første tilfeldig genererte rute. Dette viser forhåpentligvis hvor praktisk denne relativt enkle algoritmen er når den brukes på visse typer optimaliseringsproblemer.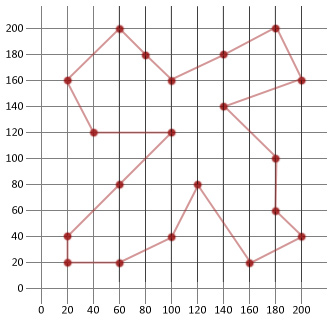
Forfatter
 Hei, Jeg Er Lee.
Hei, Jeg Er Lee.jeg er en utvikler FRA STORBRITANNIA som elsker teknologi og forretning. Her finner du artikler og veiledninger om ting som interesserer meg. Hvis du vil ansette meg eller vite mer om meg, gå over til min om meg-side