TERMISK LEDNINGSEVNE

Termisk ledningsevne av faste stoffer er av forskjellig art avhengig av om de er ledere eller ikke. I dielektrikum uten gratis elektriske ladninger overføres termisk energi av fononer. De kollektive vibrasjonene av atomer i krystallgitter har form av forskyvningsbølger, hvor forstyrrelsen genererer bølgepakker, dvs. fononer. Forskyvningsbølgene gir svingninger i tetthet som kan manifesteres som en variasjon av brytningsindeksen. Hvis bølgene passerer gjennom en region der brytningsindeksen er forskjellig fra den gjennomsnittlige volumetriske verdien, vil de etterfølgende forskyvningsbølgene som bærer energien til termisk bevegelse, bli spredt.

spredningen er jo sterkere, jo mer maksimal avvik av atomer fra deres gjennomsnittlige posisjoner i gitteret, dvs. jo høyere T. Dette står for det eksperimentelt etablerte faktum at termisk ledningsevne av krystalldielektrikum reduseres ved ganske høye temperaturer: λ 1 / T (Figur 1).

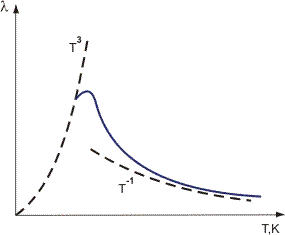
Figur 1. Variasjon av termisk ledningsevne av krystalldielektrikum med temperatur.

Debye ga et innblikk i en topplignende karakter av λ (T) variasjon ved lav T innenfor rammen av kvantemekaniske konsepter. Han utarbeidet en dipolteori for dielektrikum basert på konseptet av et molekyl som en stiv dipol. I Denne modellen Introduserte Debye konseptet Med Den såkalte Debye temperatur θ proporsjonal med maksimal frekvens av atomvibrasjoner i et fast stoff. For de fleste stoffer er θ enten lavere enn eller nær romtemperaturen(et unntak er diamant for hvilken θ = 1850 K og berrylium for hvilken θ = 1160K).

i kvanteteorien om faste stoffer betraktes krystallgitteret som et volum fylt med fonongass som fradraget av den enkleste kinetiske teorien blir brukt på

hvor c er varmekapasiteten til et dielektrisk som sammenfaller med fonongassens, v er gjennomsnittshastigheten til fononer omtrent lik lydhastigheten, den gjennomsnittlige frie banen til fononer. Eksistensen av en viss endelig verdi påer resultatet av fononspredning på fononer, på defekter av krystallgitter og spesielt på korngrenser over hele prøven. Temperaturavhengigheten λ (T) bestemmes avog c på temperatur.

ved høye temperaturer som vesentlig overstiger Debye-temperaturen, er den grunnleggende mekanismen som begrenser en fonon-fononspredning på grunn av anharmonisitet av atomvibrasjoner i en krystall. Phonon-phonon-mekanismen for termisk motstand ((1/λ) er kjent som koeffisienten for termisk motstand) er bare mulig på grunn av en overgang som resulterer i retardasjon av fononstrømmen og merkbar endring av kvasi-momentum. Jo høyere T, jo høyere er sannsynligheten for overgangen med avtagende:(1/T). Siden på T > θ varmekapasitet c øker bare litt med temperatur, derfor λ 1 / T.

ved temperaturer lavere Enn Debye-temperaturen, t<<θ, øker lengden på den gjennomsnittlige frie banenbestemt av phonon-phonon-spredning drastisk, expθ / T og er som regel begrenset til størrelsen på en krystall R. i Henhold Til Debye-loven varierer varmekapasiteten c i dette temperaturområdet som c (T/θ)3. Følgelig må koeffisienten for termisk konduktivitetskoeffisient for t3 reduseres i forhold Til t3. Temperaturen som varmeledningsevnen har en topp for, bestemmes fra ≈ R, som vanligvis tilsvarer t ≤ 0.05 θ

denne teorien står også for oppførselen av koeffisienten av termisk ledningsevne for amorfe stoffer som ikke har noen langtrekkende rekkefølge, dvs. størrelsen på deres «krystaller» er av rekkefølgen av atomstørrelser. I kraft av dette må spredning ved «grenser» av disse stoffene seire i det Hele Tatt T og≈ const. Koeffisienten av termisk ledningsevne av amorfe stoffer λT3 ved lave temperaturer og må vokse litt, i forhold til varmekapasitet, ved moderate og høye temperaturer, T > θ.

Alt dette gir en kvalitativ forklaring på avhengigheten λ (T) i ekte krystalldielektrikum, men tar ingen hensyn til avvik fra det konstante gitteret på grunn av atomiske urenheter av andre elementer og deres egne isotoper. Ved høy temperatur er motstanden som tilbys av urenheter til varmetransport uavhengig av temperatur. Dette gjør det mulig å estimere graden av krystallrenhet fra variasjon av termisk ledningsevne med temperatur. Det samme faktum gjør det mulig for oss å bestemme fordelingen mellom glassaktig og krystallstoff i det naturlige mineral hvis glasset betraktes som en urenhet i en krystall.

Termisk ledningsevne i metaller avhenger av bevegelse og samspill av nåværende bærere, dvs. ledningselektroner. Generelt koeffisient av termisk konduktivitet λ av et metall er lik summen av gitteret (fonon) λph, og elektron λe-komponenter, λ = λe + λph; ved vanlige temperaturer, som en regel, λe >>λph.

hvis vi bruker en enkel kinetisk teori om gasser til strømmen av frie elektroner og antar at lengden på deres frie bane ikke er avhengig av hastighet, innebærer teorien at

hvor e er elektronladningen, K Boltzrnanns konstant, og σ elektrisk ledningsevne. En streng kvantemekanisk teori gir et lignende forhold,

i begge formlene ser forholdet mellom elektrondelen av koeffisienten av termisk ledningsevne hryvnias til elektrisk ledningsevne hryvnias, i et bredt temperaturområde, ut til å være i forhold til temperaturen i Henhold Til wiedemann-Franz-loven, λ/σ = LT, der L er Lorentz-nummeret. Denne loven brukes til å beregne λ fra den målte elektriske ledningsevnen. Det brytes imidlertid ved temperaturer under θ når en elektron-fononinteraksjon hersker (σ vokser med avtagende T som T-5 mens le varierer litt som T−2).

de eksperimentelle funnene viser at termisk ledningsevne av metaller ved høye temperaturer som regel er en litt avtagende funksjon av temperaturen. Men det er mange unntak. Dermed reduseres termisk ledningsevne av jern sterkt med temperatur mens tantal og niob viser en positiv temperaturkoeffisient.

av interesse er forsøkene på å sammenligne koeffisientene for termisk ledningsevne for forskjellige stoffer for en enkelt karakteristisk temperatur, for eksempel for smeltepunktet Tm av faste stoffer. Dermed har den statistiske behandlingen av eksperimentelle data utført Av Missenard vist at termisk ledningsevne av metaller ved smeltepunktet λ(T = Tm) = λ er i forhold til λog termisk ledningsevne av dielektriske krystaller ved T = Tm er i forhold til, der m er molekylmassen, N antall atomer i kjemisk formel, ρ tettheten og smeltepunktet Tm er I Kelvins.

varmetransport i halvledere er mer kompleks enn i dielektrikum og metaller fordi fononet og elektronkomponentene er like viktige for dem. En annen grunn til kompleksiteten er den betydelige effekten av urenheter, bipolar diffusjon og andre lite studerte faktorer på varmeoverføring.

effekten av trykk på termisk ledningsevne av faste stoffer kan antas, med god nøyaktighet, å være lineær, λ for mange metaller som vokser med p.

For effekten av porøsitet på termisk ledningsevne av faste stoffer, se Porøst Medium.