dowiedz się OpenCV

w tym poście poznamy szczegóły histogramu deskryptora funkcji zorientowanych gradientów (HOG). Dowiemy się, co jest pod maską i jak ten deskryptor jest obliczany wewnętrznie przez OpenCV, MATLAB i inne pakiety.

ten post jest częścią serii, którą piszę na temat rozpoznawania obrazów i wykrywania obiektów.

pełna lista tutoriali z tej serii znajduje się poniżej:

1. rozpoznawanie obrazów przy użyciu tradycyjnych technik widzenia komputerowego : Część 1
2. Histogram zorientowanych gradientów : część 2
3. przykładowy kod rozpoznawania obrazu : Część 3
4. Szkolenie lepszego detektora oka: część 4a
5. wykrywanie obiektów przy użyciu tradycyjnych technik wizyjnych : część 4b
6. jak trenować i testować własny detektor obiektów OpenCV : Część 5
7. rozpoznawanie obrazów za pomocą głębokiego uczenia : Część 6
   • Wprowadzenie do sieci neuronowych
   • zrozumienie sieci neuronowych Feedforward
   • rozpoznawanie obrazów za pomocą Konwolucyjnych sieci neuronowych
8. wykrywanie obiektów za pomocą głębokiego uczenia: Część 7

wiele rzeczy wygląda na trudne i tajemnicze. Ale kiedy poświęcisz trochę czasu na ich dekonstrukcję, tajemnica zostaje zastąpiona przez mistrzostwo i to jest to, czego szukamy. Jeśli jesteś początkujący i uważasz, że komputerowe widzenie jest trudne i tajemnicze, pamiętaj o następującym

P : Jak zjeść słonia ?
A : Jeden kęs na raz!

co to jest deskryptor funkcji?

deskryptor funkcji to reprezentacja obrazu lub poprawki obrazu, która upraszcza obraz poprzez wyodrębnianie użytecznych informacji i wyrzucanie obcych informacji.

zazwyczaj deskryptor funkcji konwertuje obraz o rozmiarze szerokość x wysokość x 3 (kanały) na wektor funkcji / tablicę długości N. W przypadku deskryptora funkcji Wieprza obraz wejściowy ma rozmiar 64 x 128 x 3, a wektor funkcji wyjściowej ma długość 3780.

pamiętaj, że deskryptor Wieprza można obliczyć dla innych rozmiarów, ale w tym poście trzymam się liczb przedstawionych w oryginalnym artykule, abyś mógł łatwo zrozumieć koncepcję za pomocą jednego konkretnego przykładu.

to wszystko brzmi dobrze, ale co jest „przydatne”, a co” obce”? Aby zdefiniować „przydatne”, musimy wiedzieć, do czego jest” przydatne”? Oczywiście wektor funkcji nie jest przydatny do oglądania obrazu. Ale jest to bardzo przydatne do zadań, takich jak rozpoznawanie obrazów i wykrywanie obiektów. Wektor funkcji wytwarzany przez te algorytmy po wprowadzeniu do algorytmów klasyfikacji obrazów, takich jak maszyna wektorów pomocniczych (SVM), daje dobre wyniki.

ale jakie „funkcje” są przydatne do zadań klasyfikacyjnych ? Omówmy ten punkt na przykładzie. Załóżmy, że chcemy zbudować detektor obiektów, który wykrywa guziki koszul i płaszczy.

przycisk jest okrągły ( może wyglądać eliptycznie na zdjęciu ) i zwykle ma kilka otworów do szycia. Można uruchomić detektor krawędzi na obrazie przycisku i łatwo stwierdzić, czy jest to Przycisk, po prostu patrząc na obraz krawędzi. W tym przypadku informacje o krawędziach są „przydatne”, a informacje o kolorze nie. Ponadto cechy muszą mieć również siłę rozróżniającą. Na przykład dobre funkcje wyodrębnione z obrazu powinny odróżniać przyciski od innych okrągłych obiektów, takich jak monety i opony samochodowe.

w deskryptorze funkcji Wieprza jako cechy stosuje się rozkład ( histogramy ) kierunków gradientów ( zorientowanych gradientów). Gradienty (pochodne x i y ) obrazu są użyteczne, ponieważ wielkość gradientów wokół krawędzi i narożników jest duża (obszary nagłych zmian intensywności) i wiemy, że krawędzie i narożniki zawierają o wiele więcej informacji na temat kształtu obiektu niż obszary płaskie.

jak obliczyć Histogram gradientów zorientowanych ?

w tej sekcji przejdziemy do szczegółów obliczania deskryptora funkcji Wieprza. Aby zilustrować każdy krok, użyjemy łatki obrazu.

Krok 1 : Preprocessing

jak wspomniano wcześniej, deskryptor funkcji HOG używany do wykrywania pieszych jest obliczany na łacie 64×128 obrazu. Oczywiście obraz może mieć dowolny rozmiar. Zazwyczaj łaty w wielu skalach są analizowane w wielu lokalizacjach obrazu. Jedynym ograniczeniem jest to, że analizowane łaty mają stały współczynnik kształtu. W naszym przypadku łaty muszą mieć proporcje 1: 2. Na przykład mogą to być 100×200, 128×256 lub 1000×2000, ale nie 101×205.

aby zilustrować ten punkt pokazałem duży obraz o rozmiarze 720×475. Wybraliśmy łatkę o rozmiarze 100×200 do obliczenia naszego deskryptora funkcji Wieprza. Ta poprawka jest przycinana z obrazu i zmieniana na 64×128. Teraz jesteśmy gotowi obliczyć deskryptor Wieprza dla tej poprawki obrazu.

artykuł Dalala i Triggsa również wspomina o korekcji gamma jako kroku wstępnego przetwarzania, ale wzrost wydajności jest niewielki, więc pomijamy ten krok.

Krok 2: Oblicz obrazy gradientu

aby obliczyć deskryptor Wieprza, musimy najpierw obliczyć gradienty poziome i pionowe; w końcu chcemy obliczyć histogram gradientów. Można to łatwo osiągnąć, filtrując obraz za pomocą następujących jąder.

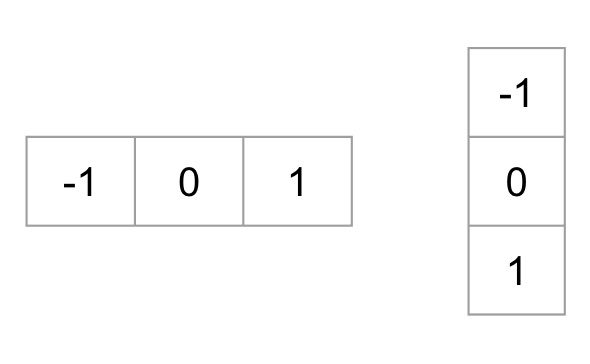
możemy również osiągnąć te same wyniki, używając operatora Sobel w OpenCV o rozmiarze jądra 1.

// C++ gradient calculation.// Read imageMat img = imread("bolt.png");img.convertTo(img, CV_32F, 1/255.0);// Calculate gradients gx, gyMat gx, gy;Sobel(img, gx, CV_32F, 1, 0, 1);Sobel(img, gy, CV_32F, 0, 1, 1);

# Python gradient calculation # Read imageim = cv2.imread('bolt.png')im = np.float32(im) / 255.0# Calculate gradientgx = cv2.Sobel(img, cv2.CV_32F, 1, 0, ksize=1)gy = cv2.Sobel(img, cv2.CV_32F, 0, 1, ksize=1)

następnie możemy znaleźć wielkość i kierunek gradientu za pomocą następującego wzoru

jeśli używasz OpenCV, obliczenia można wykonać za pomocą funkcji cartToPolar, jak pokazano poniżej.

// C++ Calculate gradient magnitude and direction (in degrees)Mat mag, angle;cartToPolar(gx, gy, mag, angle, 1);

ten sam kod w Pythonie wygląda tak.

# Python Calculate gradient magnitude and direction ( in degrees )mag, angle = cv2.cartToPolar(gx, gy, angleInDegrees=True)

poniższy rysunek pokazuje gradienty.

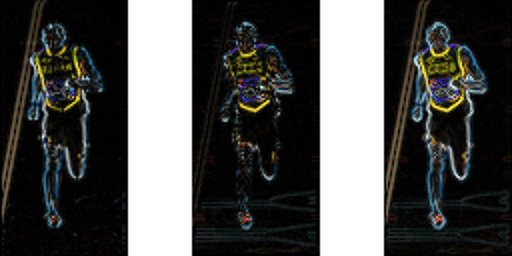
zauważ, że gradient x jest uruchamiany na liniach pionowych, a gradient y na liniach poziomych. Wielkość gradientu rozpala się tam, gdzie kiedykolwiek nastąpiła gwałtowna zmiana intensywności. Żaden z nich nie strzela, gdy region jest gładki. Celowo pominąłem obraz pokazujący kierunek gradientu, ponieważ kierunek pokazany jako obraz nie przekazuje wiele.

gradientowy obraz usunął wiele nieistotnych informacji ( np. stałe kolorowe tło ), ale podświetlone kontury. Innymi słowy, możesz spojrzeć na obraz gradientu i nadal łatwo powiedzieć, że na zdjęciu jest osoba.

przy każdym pikselu gradient ma wielkość i kierunek. W przypadku obrazów kolorowych ocenia się gradienty trzech kanałów (jak pokazano na rysunku powyżej ). Wielkość gradientu w pikselu jest maksymalną wielkością gradientów trzech kanałów, a kąt jest kątem odpowiadającym maksymalnemu gradientowi.

Krok 3: Oblicz Histogram gradientów w komórkach 8×8

w tym kroku obraz jest podzielony na komórki 8×8 i histogram gradientów jest obliczany dla każdej komórki 8×8.

o histogramach dowiemy się za chwilę, ale zanim tam pójdziemy, najpierw zrozumiemy, dlaczego podzieliliśmy obraz na komórki 8×8. Jednym z ważnych powodów użycia deskryptora funkcji do opisania poprawki obrazu jest to, że zapewnia on zwartą reprezentację. Poprawka obrazu 8×8 zawiera wartości 8x8x3 = 192 pikseli. Gradient tej poprawki zawiera 2 wartości (wielkość i kierunek) na piksel, co daje 8x8x2 = 128 liczb.

pod koniec tej sekcji zobaczymy, jak te 128 liczb są reprezentowane za pomocą 9-binowego histogramu, który może być przechowywany jako tablica 9 liczb. Reprezentacja jest nie tylko bardziej zwarta, ale także obliczanie histogramu nad łatą sprawia, że ta represenacja jest bardziej odporna na hałas. Poszczególne graidenty mogą mieć szum, ale histogram ponad 8×8 plastrów sprawia, że reprezentacja jest znacznie mniej wrażliwa na szum.

ale dlaczego 8×8 patch ? Dlaczego nie 32×32 ? Jest to wybór projektu podyktowany skalą funkcji, których szukamy. Wieprz był początkowo używany do wykrywania pieszych. Komórki 8×8 na zdjęciu pieszego o wymiarach 64×128 są wystarczająco duże, aby uchwycić ciekawe cechy (np. twarz, czubek głowy itp. ).

histogram jest w zasadzie wektorem (lub tablicą) 9-ciu liczb (liczb ) odpowiadających kątom 0, 20, 40, 60 … 160.

spójrzmy na jedną łatkę 8×8 na obrazie i zobaczmy, jak wyglądają gradienty.

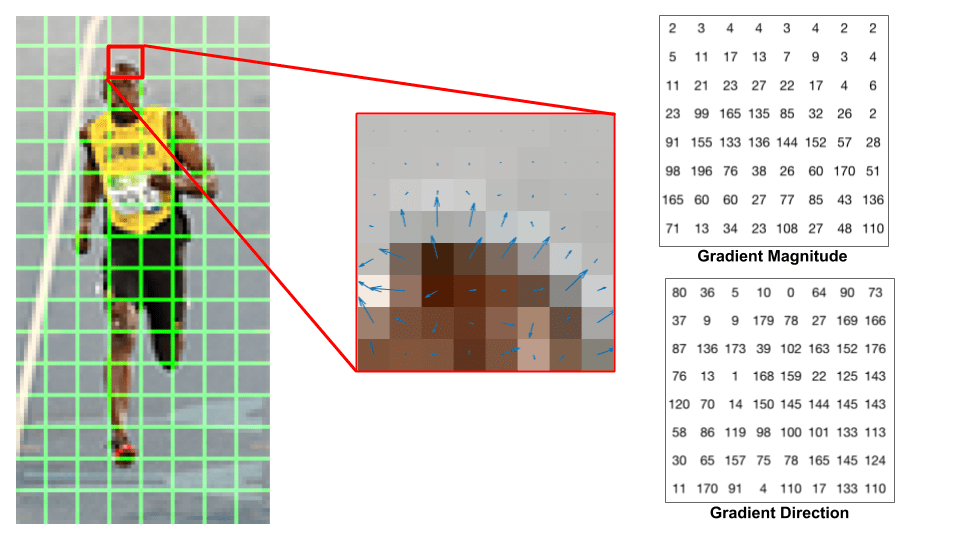
jeśli jesteś początkującym w wizji komputerowej, obraz w centrum jest bardzo pouczający. Pokazuje on skrawek obrazu pokryty strzałkami pokazującymi gradient-strzałka pokazuje kierunek gradientu, a jej długość pokazuje wielkość. Zauważ, jak kierunek strzałek wskazuje na kierunek zmiany intensywności, a wielkość pokazuje, jak duża jest różnica.

po prawej stronie widzimy surowe liczby reprezentujące gradienty w komórkach 8×8 z jedną niewielką różnicą — kąty wynoszą od 0 do 180 stopni zamiast od 0 do 360 stopni. Są to gradienty „niepodpisane”, ponieważ gradient i jego wartość ujemna są reprezentowane przez te same liczby. Innymi słowy, strzałka gradientu i jeden 180 stopni naprzeciwko niej są uważane za takie same. Ale dlaczego nie użyć 0-360 stopni ?

empirycznie wykazano, że niepodpisane gradienty działają lepiej niż podpisane gradienty w przypadku wykrywania pieszych. Niektóre implementacje HOG pozwolą Ci określić, czy chcesz używać podpisanych gradientów.

następnym krokiem jest utworzenie histogramu gradientów w tych komórkach 8×8. Histogram zawiera 9 pojemników odpowiadających kątom 0, 20, 40 … 160. Poniższy rysunek ilustruje proces. Patrzymy na wielkość i kierunek gradientu tego samego plastra 8×8, Jak na poprzednim rysunku.

kosz jest wybierany na podstawie kierunku, a głos ( wartość, która trafia do kosza ) jest wybierany na podstawie wielkości. Najpierw skupmy się na pikselu otoczonym kolorem niebieskim. Ma kąt (kierunek) 80 stopni i wielkość 2. Dodajemy 2 do piątego pojemnika. Gradient w pikselu otoczonym kolorem czerwonym ma kąt 10 stopni i wielkość 4. Ponieważ 10 stopni jest w połowie drogi między 0 a 20, głos piksela dzieli się równomiernie na dwa pojemniki.

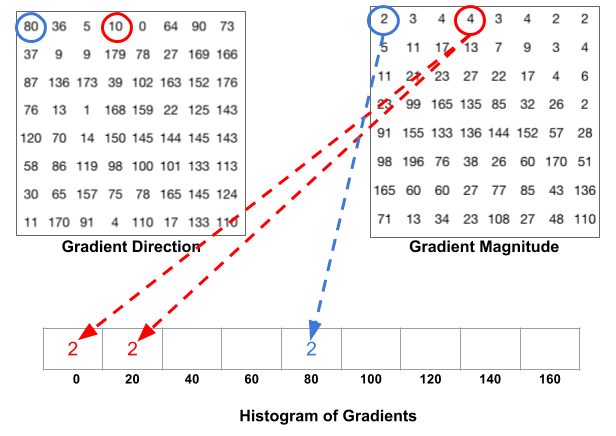
jest jeszcze jeden szczegół, o którym należy pamiętać. Jeśli kąt jest większy niż 160 stopni, to jest między 160 A 180 i wiemy, że kąt zawija się wokół, co równa się 0 i 180. Tak więc w poniższym przykładzie piksel o kącie 165 stopni przyczynia się proporcjonalnie do kosza 0 stopni i kosza 160 stopni.

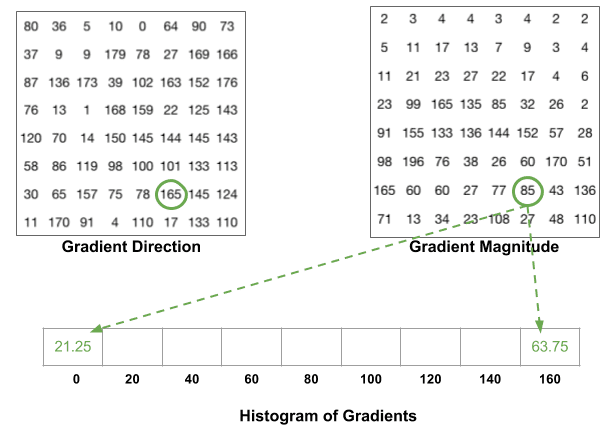
wkład wszystkich pikseli w komórkach 8×8 jest dodawany w celu utworzenia histogramu 9-bin. Na powyższym patchu wygląda to tak

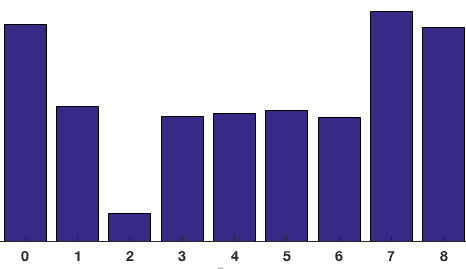
w naszej reprezentacji, oś y wynosi 0 stopni. Widać, że histogram ma dużą wagę w pobliżu 0 i 180 stopni, co jest po prostu innym sposobem na powiedzenie, że w łatce gradienty są skierowane w górę lub w dół.

Krok 4 : Normalizacja 16×16 bloków

w poprzednim kroku stworzyliśmy histogram na podstawie gradientu obrazu. Gradienty obrazu są wrażliwe na ogólne oświetlenie. Jeśli obraz będzie ciemniejszy przez podzielenie wszystkich wartości pikseli przez 2, wielkość gradientu zmieni się o połowę, a zatem wartości histogramu zmienią się o połowę.

najlepiej, aby nasz deskryptor był niezależny od wariantów oświetlenia. Innymi słowy, chcielibyśmy „znormalizować” histogram, aby nie miały na niego wpływu zmiany oświetlenia.

zanim wyjaśnię, jak histogram jest znormalizowany, zobaczmy, jak wektor o długości 3 jest znormalizowany.

powiedzmy, że mamy wektor kolorów RGB . Długość tego wektora to $\sqrt{128^2 + 64^2 + 32^2} = 146.64$. Jest to również nazywane normą L2 wektora. Podzielenie każdego elementu tego wektora przez 146,64 daje nam wektor znormalizowany .

rozważmy teraz inny wektor, w którym elementy są dwukrotnie większe od wartości pierwszego wektora 2 x = . Możesz sam to wypracować, aby zobaczyć, że spowoduje to normalizację, która jest taka sama jak znormalizowana wersja oryginalnego wektora RGB. Widać, że normalizacja wektora usuwa skalę.

teraz, gdy wiemy, jak normalizować wektor, możesz pokusić się o myślenie, że podczas obliczania Wieprza można po prostu normalizować histogram 9×1 w ten sam sposób, w jaki znormalizowaliśmy wektor 3×1 powyżej. Nie jest to zły pomysł, ale lepszym pomysłem jest normalizacja na większym bloku o wymiarach 16×16.

blok 16×16 ma 4 histogramy, które można połączyć, tworząc wektor 36 x 1 elementu i można go znormalizować tak, jak wektor 3×1 jest znormalizowany. Okno jest następnie przesuwane o 8 pikseli (patrz animacja) i znormalizowany wektor 36×1 jest obliczany nad tym oknem i proces jest powtarzany.

Krok 5: Oblicz wektor funkcji Wieprza

aby obliczyć końcowy wektor funkcji dla całej poprawki obrazu, wektory 36×1 są połączone w jeden olbrzymi wektor. Jaka jest wielkość tego wektora ? Obliczmy

1. ile mamy pozycji bloków 16×16 ? Istnieje 7 pozycji poziomych i 15 pionowych, co daje w sumie 7 x 15 = 105 pozycji.
2. każdy blok 16×16 jest reprezentowany przez wektor 36×1. Więc kiedy połączymy je wszystkie w jeden wektor gainta otrzymamy wektor wymiarowy 36×105 = 3780.

Wizualizacja histogramu zorientowanych gradientów

deskryptor Wieprza obrazu jest zwykle wizualizowany przez wykreślenie znormalizowanych histogramów 9×1 w komórkach 8×8. Zobacz zdjęcie z boku. Zauważysz, że dominujący kierunek histogramu rejestruje kształt osoby, zwłaszcza wokół tułowia i nóg.

niestety, nie ma łatwego sposobu na wizualizację deskryptora Wieprza w OpenCV.

Subskrybuj & Pobierz Kod