
dla koncepcji identyfikacji cyfry jednostkowej musimy najpierw zapoznać się z pojęciem cykliczności. Cykliczność dowolnej liczby jest o ostatniej cyfrze i jak pojawiają się w określony sposób. Weźmy przykład, aby to wyczyścić:
Wykres cykliczności z 2 wynosi:
21 =2
22 =4
23 =8
24=16
25=32
przyjrzyj się temu bliżej. Widać, że gdy 2 jest mnożona za każdym razem przez własne ja, ostatnia cyfra się zmienia. W czwartym mnożeniu 25 mA tę samą cyfrę jednostkową co 21. To pokazuje nam, że cykliczność 2 równa się 4, czyli po co czwartym mnożyciu, cyfra jednostkowa będzie równa 2.
tabela cykliczności:
tabela cykliczności dla liczb jest podana jak poniżej:
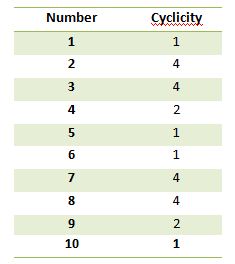
jak obliczyliśmy powyższe? Pomnóż i przekonaj się sam. To dobra praktyka.
teraz użyjmy pojęcia cykliczności do obliczenia cyfry jednostkowej liczby.
jaka jest cyfra jednostkowa wyrażenia 4993?
teraz mamy dwie metody, aby to rozwiązać, ale wybieramy najlepszy sposób, aby to rozwiązać, tj. poprzez cykliczność
wiemy, że cykliczność 4 to 2
Spójrz:
41 =4
42 =16
43 =64
44 =256
z góry widać, że cykliczność 4 wynosi 2. Teraz z liczbą cykliczności tj. z 2 podzielić daną moc tj. 993 przez 2 Jaka będzie reszta reszta będzie 1 więc odpowiedź gdy 4 podniesione do potęgi jedynki wynosi 4.Cyfrą jednostkową w tym przypadku jest 4.
aby sprawdzić, czy nauczyłeś się tematu, pomyśl o dowolnej liczbie w ten sposób, Oblicz jej cyfrę jednostkową, a następnie sprawdź ją za pomocą kalkulatora.
Uwaga: jeśli reszta w każdym przypadku stanie się zerowa, to cyfra jednostkowa będzie ostatnią cyfrą liczby acykliczności
gdzie A jest liczbą podaną, a liczba cykliczności jest pokazana na powyższym rysunku.
rozwiążmy inny przykład:
cyfra w miejscu jednostki liczby 7295 X 3158 to
A. 7
B. 2
C. 6
D. 4
rozwiązanie
tabela cykliczności dla 7 wygląda następująco:
71 =7
72 =49
73 = 343
74 = 2401
Podzielmy 295 przez 4, a reszta to 3.
tak więc ostatnia cyfra 7295 jest równa ostatniej cyfrze 73, czyli 3.
tabela cykliczności dla 3 wygląda następująco:
31 =3
32 =9
33 = 27
34 = 81
35 = 243
Podzielmy 158 przez 4, reszta to 2. Stąd ostatnią cyfrą będzie 9.
zatem cyfra jednostkowa (7925 X 3158) jest cyfrą jednostkową iloczynu cyfry w miejscu jednostki 7925 i 3158 = 3 * 9 = 27. Stąd opcja 1 jest odpowiedzią.
