zacząłem robić popularny kurs uczenia maszynowego Andrew Ng na Coursera. Pierwszy tydzień obejmuje wiele, przynajmniej dla kogoś, kto nie dotknął wiele rachunku różniczkowego od kilku lat
- funkcje kosztowe (średnia różnica do kwadratu)
- spadek gradientu
- regresja liniowa
te trzy tematy były bardzo ważne. Opowiem szczegółowo o każdym z nich i o tym, jak do siebie pasują, z odrobiną kodu Pythona do zademonstrowania.
Edytuj 4 maja: Opublikowałem kontynuację skupiającą się na tym, jak działa funkcja kosztów, w tym intuicję, jak obliczyć ją ręcznie i dwie różne implementacje Pythona. Mogę zrobić Spadanie gradientowe, a następnie połączyć je w regresję liniową.
Reprezentacja modelu
po pierwsze, celem większości algorytmów uczenia maszynowego jest skonstruowanie modelu: hipotezy, która może być wykorzystana do oszacowania Y na podstawie X. hipoteza lub model mapuje wejścia na wyjścia. Na przykład, powiedzmy, że trenuję model oparty na danych dotyczących mieszkania, które zawierają Rozmiar domu i cenę sprzedaży. Szkoląc model, mogę dać Ci oszacowanie, za ile możesz sprzedać swój dom w oparciu o jego rozmiar. Jest to przykład problemu regresji-biorąc pod uwagę pewne dane wejściowe, chcemy przewidzieć ciągłe dane wyjściowe.
hipoteza jest zwykle przedstawiana jako

wartości theta są parametrami.
kilka szybkich przykładów jak wizualizujemy hipotezę:
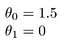
daje to h (x) = 1,5 + 0x. 0x oznacza brak nachylenia, a y zawsze będzie stałą 1.5. To wygląda jak:

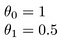

celem stworzenia modelu jest wybranie parametrów lub wartości theta, tak aby h(x) był bliski y dla danych treningowych, x i y. Więc dla tych danych
x =
y =

postaram się znaleźć linię najlepiej dopasowaną za pomocą regresji liniowej. Zaczynajmy.
funkcja kosztowa
potrzebujemy funkcji, która zminimalizuje parametry nad naszym zestawem danych. Jedną z często używanych funkcji jest średni błąd kwadratowy, który mierzy różnicę między estymatorem (zestawem danych) a wartością szacunkową (prognozą). Wygląda to tak:

okazuje się, że możemy trochę dostosować równanie, aby obliczenie w dół ścieżki było nieco prostsze. Kończymy z:
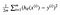
zastosujmy tę funkcję const do następujących danych:

na razie obliczymy niektóre wartości theta i ręcznie wykreślimy funkcję kosztową. Ponieważ ta funkcja przechodzi przez (0, 0), patrzymy tylko na jedną wartość theta. Od tej chwili będę odnosił się do funkcji kosztowej jako j (Θ).
dla J(1) otrzymujemy 0. Nic dziwnego — wartość J(1) daje prostą, która idealnie pasuje do danych. A może J(0.5)?

funkcja MSE daje nam wartość 0.58. Narysujmy obie nasze wartości do tej pory:
J(1) = 0
J (0.5) = 0.58

przeliczę jeszcze kilka wartości j (Θ).

i jeśli ładnie połączymy kropki…

możemy zobaczyć, że funkcja kosztowa jest na minimum, gdy theta = 1. To ma sens – nasze początkowe dane to linia prosta o nachyleniu 1 (pomarańczowa linia na rysunku powyżej).
spadek gradientu
minimalizowaliśmy j(Θ) metodą prób i błędów powyżej — po prostu próbowaliśmy wielu wartości i wizualnie sprawdzaliśmy uzyskany Wykres. Musi być lepszy sposób? Kolejka spadek gradientu. Gradient Descent jest ogólną funkcją minimalizującą funkcję, w tym przypadku średnią kwadratową funkcją kosztu błędu.
Gradient Descent po prostu robi to, co robiliśmy ręcznie — zmienia wartości theta lub parametry, krok po kroku, aż mamy nadzieję, że osiągniemy minimum.
zaczynamy od inicjalizacji theta0 i theta1 do dowolnych dwóch wartości, powiedzmy 0 dla obu i od tego przechodzimy. Formalnie algorytm wygląda następująco:

gdzie α, Alfa, to szybkość uczenia się, czyli jak szybko chcemy osiągnąć minimum. Jeśli jednak α jest zbyt duży, możemy go przekroczyć.

łącząc to wszystko — regresja liniowa
szybko podsumowując:
mamy hipotezę:

która musi pasować do naszych danych treningowych. Możemy użyć funkcji kosztowej, takiej jak średni błąd Kwadratowy:

, który możemy zminimalizować za pomocą spadku gradientu:

, który prowadzi nas do naszego pierwszego algorytmu uczenia maszynowego, regresji liniowej. Ostatnim elementem układanki, który musimy rozwiązać, aby mieć działający model regresji liniowej, jest częściowa pochodna funkcji kosztu:
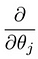
co okazuje się być:
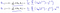
co daje nam regresję liniową!
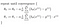
z teorią na uboczu, przejdę do implementacji tej logiki w Pythonie w następnym poście.
Edycja 4 maja: opublikowałem kontynuację skupiającą się na tym, jak działa tutaj funkcja kosztów, w tym intuicja, jak obliczyć ją ręcznie i dwie różne implementacje Pythona. Mogę zrobić Spadanie gradientowe, a następnie połączyć je w regresję liniową.