pole elektryczne E zawsze można wyrazić jako gradient funkcji potencjału skalarnego
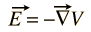
nie ma ogólnego potencjału skalarnego dla pola magnetycznego B, ale można go wyrazić jako zwinięcie funkcji wektorowej
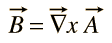
ta funkcja A ma nazwę „potencjał wektorowy”, ale nie jest bezpośrednio związana z działaniem takim, jakim jest potencjał skalarny.
potencjał wektorowy jest zdefiniowany jako zgodny z Prawem Ampere ’ a i może być wyrażony albo w postaci prądu i, albo gęstości prądu j (źródła pola magnetycznego). W różnych tekstach definicja ta przyjmuje formy
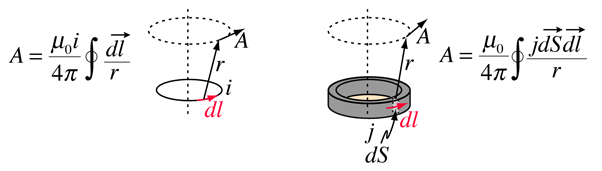
jednym z przesłanek dla potencjału wektorowego jest to, że łatwiej jest obliczyć potencjał wektorowy niż obliczyć pole magnetyczne bezpośrednio z danej geometrii prądowej źródła. Jego najczęstszym zastosowaniem jest teoria anten i opis fal elektromagnetycznych.
ponieważ pole magnetyczne B jest zdefiniowane jako zwijanie a, a przez tożsamość wektorową zwijanie gradientu jest identyczne zerem, to dowolna Dowolna funkcja, która może być wyrażona jako gradient funkcji skalarnej, może być dodana do a bez zmiany wartości b uzyskanej z niego. Oznacza to, że A’ można dowolnie zastąpić a gdzie
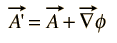
takie transformacje nazywane są transformacjami mierników, i było wiele „mierników”, które zostały wykorzystane do korzyści jest konkretne rodzaje obliczeń w teorii elektromagnetycznej.