Przewodność cieplna

przewodność cieplna ciał stałych ma inny charakter w zależności od tego, czy są przewodnikami, czy nie. W dielektrykach bez wolnych ładunków elektrycznych energia cieplna przekazywana jest przez fonony. Kolektywne drgania atomów w sieci krystalicznej przybierają formę fal przemieszczeń, których interferencja generuje Pakiety falowe, czyli fonony. Fale przemieszczeń powodują wahania gęstości, które mogą objawiać się zmiennością współczynnika załamania światła. Jeśli fale przechodzą przez obszar, w którym współczynnik załamania różni się od średniej wartości objętościowej, kolejne fale przemieszczenia przenoszące energię ruchu termicznego zostaną rozproszone.

rozpraszanie jest silniejsze, im większe jest maksymalne odchylenie atomów od ich średnich pozycji w sieci, tj. Wynika to z doświadczalnie ustalonego faktu, że przewodność cieplna dielektryków krystalicznych zmniejsza się w dość wysokich temperaturach: λ1/T (Rysunek 1).

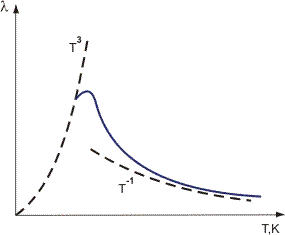
Rysunek 1. Zmiana przewodności cieplnej dielektryków kryształowych w zależności od temperatury.

Debye dał wgląd w szczytowy charakter zmiany λ(T) przy niskim T w ramach koncepcji mechaniki kwantowej. Opracował dipolową teorię dielektryków opartą na koncepcji cząsteczki jako sztywnego dipola. W tym modelu Debye wprowadził koncepcję tzw. temperatury Debye ’ a θD proporcjonalnej do maksymalnej częstotliwości drgań atomowych w ciele stałym. Dla większości substancji θD jest niższa lub bliska temperaturze pokojowej (wyjątkiem jest diament, dla którego θD = 1850 K i berrylium, dla którego θD = 1160k).

w kwantowej teorii ciał stałych sieć krystaliczna jest uważana za objętość wypełnioną gazem fononowym, do której stosuje się najprostszą teorię kinetyczną

gdzie c jest pojemnością cieplną dielektryka, która pokrywa się z pojemnością gazu fononowego, v średnią prędkością fononów w przybliżeniu równą prędkości dźwięku,średnią swobodną ścieżką fononów. Istnienie pewnej skończonej wartościjest wynikiem rozpraszania fononu na fononach, na defektach sieci krystalicznej, a w szczególności na granicach ziaren na całej okazie. Zależność temperaturową λ(T) określa się przez zależnośći c od temperatury.

w wysokich temperaturach znacznie przekraczających temperaturę Debye ’ a θD, podstawowym mechanizmem ograniczającym jest rozpraszanie fononu z powodu anharmoniczności drgań atomów w krysztale. Fonon-fononowy mechanizm oporu termicznego ((1 / λ) znany jest jako współczynnik oporu termicznego) jest możliwy do zrealizowania tylko dzięki przemianie powodującej opóźnienie przepływu fononu i znaczną zmianę quasi-pędu. Im wyższy t, tym większe prawdopodobieństwo przejścia z maleje:(1/T). Ponieważ przy T > θD pojemność cieplna c tylko nieznacznie wzrasta wraz z temperaturą, stąd λ1/T.

w temperaturach niższych niż temperatura Debye 'a, T<<θD, długość średniej ścieżki swobodnejwyznaczonej przez rozpraszanie fononu-fononu drastycznie rośnie,expθD/t i, co do zasady, jest ograniczona do wielkości kryształu R. zgodnie z prawem Debye’ a pojemność cieplna c w tym zakresie temperatur zmienia się jako C(t/θD)3. W związku z tym przy T → 0 współczynnik przewodności cieplnej λ musi zmniejszać się proporcjonalnie do T3. Temperatura, dla której przewodność cieplna ma wartość szczytową, jest określana od≈ r, co zwykle odpowiada T ≤ 0,05 θD.

teoria ta uwzględnia również zachowanie współczynnika przewodności cieplnej dla substancji amorficznych nie mających rzędu dalekiego zasięgu, tzn. wielkość ich „kryształów” jest rzędu rozmiarów atomowych. Dzięki temu rozpraszanie na „granicach” tych substancji musi przeważać w ogóle t i≈ const. Współczynnik przewodności cieplnej substancji amorficznych λ T3 w niskich temperaturach i musi nieznacznie rosnąć, proporcjonalnie do pojemności cieplnej, w umiarkowanych i wysokich temperaturach, t > θD.

wszystko to zapewnia jakościowe Wyjaśnienie zależności λ (T) w rzeczywistych dielektrykach krystalicznych, ale nie bierze pod uwagę odchyleń od stałej siatki z powodu zanieczyszczeń atomowych innych pierwiastków i ich własnych izotopów. W wysokiej temperaturze odporność, jaką oferują zanieczyszczenia na transport ciepła, jest niezależna od temperatury. Pozwala to na oszacowanie stopnia czystości kryształu na podstawie zmiany jego przewodności cieplnej z temperaturą. Ten sam fakt pozwala nam określić rozkład pomiędzy substancją szklistą i krystaliczną w naturalnym minerale, jeśli szkło jest uważane za zanieczyszczenie w krysztale.

przewodność cieplna w metalach zależy od ruchu i interakcji nośników prądu, czyli elektronów przewodnictwa. Ogólnie rzecz biorąc, współczynnik przewodności cieplnej λ metalu jest równy sumie kraty (fononu) λph i składników elektronów λe, λ = λe + λph; w zwykłych temperaturach z reguły λe > > λph.

jeśli zastosujemy prostą kinetyczną teorię gazów do przepływu wolnych elektronów i założymy, że długość ich swobodnej drogi nie zależy od prędkości, to teoria zakłada, że

gdzie e jest ładunkiem elektronu, stałą Boltzrnanna K, A σ przewodnością elektryczną. Ścisła teoria mechaniki kwantowej oferuje podobną relację,

w obu wzorach stosunek elektronowej części współczynnika przewodności cieplnej λ do przewodności elektrycznej σ, w szerokim zakresie temperatur, wydaje się być proporcjonalny do temperatury zgodnie z prawem Wiedemanna-Franza, λ/σ = LT, gdzie L jest liczbą Lorentza. Prawo to służy do obliczenia λe na podstawie zmierzonej przewodności elektrycznej. Jest on jednak łamany w temperaturach poniżej θD, gdy przeważa interakcja elektron-fonon (σ rośnie wraz ze spadkiem T jako T-5, podczas gdy le zmienia się nieco jako T-2).

wyniki eksperymentów dowodzą, że z reguły przewodność cieplna metali w wysokich temperaturach jest nieznacznie zmniejszającą się funkcją temperatury. Ale jest wiele wyjątków. Tak więc przewodność cieplna żelaza silnie zmniejsza się wraz z temperaturą, podczas gdy tantal i niob wykazują dodatni współczynnik temperaturowy.

interesujące są próby porównania współczynników przewodności cieplnej dla różnych substancji dla jednej charakterystycznej temperatury, na przykład dla temperatury topnienia TM ciał stałych. Tak więc statystyczne przetwarzanie danych doświadczalnych przeprowadzone przez Missenard wykazało, że przewodność cieplna metali w temperaturze topnienia λ(T = Tm) = λm jest proporcjonalna do λ, a przewodność cieplna kryształów dielektrycznych w t = TM jest proporcjonalna do, gdzie M to masa cząsteczkowa, n liczba atomów we wzorze chemicznym, ρ gęstość, a temperatura topnienia TM jest w kelwinach.

transport ciepła w półprzewodnikach jest bardziej złożony niż w dielektrykach i metalach, ponieważ fonon i Komponenty elektronowe są dla nich równie istotne. Innym powodem złożoności jest znaczny wpływ zanieczyszczeń, dyfuzji dwubiegunowej i innych mało zbadanych czynników na transfer ciepła.

wpływ ciśnienia na przewodność cieplną ciał stałych można przyjąć, z dobrą dokładnością, jako liniowy, λ dla wielu metali rosnących z P.

wpływ porowatości na przewodność cieplną ciał stałych patrz porowate Medium.