znalezienie optymalnego rozwiązania pewnych problemów z optymalizacją może być niezwykle trudnym zadaniem, często praktycznie niemożliwym. Dzieje się tak dlatego, że gdy problem staje się wystarczająco duży, musimy przeszukać ogromną liczbę możliwych rozwiązań, aby znaleźć optymalne. Nawet przy nowoczesnej mocy obliczeniowej wciąż istnieje zbyt wiele możliwych rozwiązań do rozważenia. W tym przypadku, ponieważ nie możemy realistycznie oczekiwać znalezienia optymalnego w rozsądnym czasie, musimy zadowolić się czymś, co jest wystarczająco blisko.
przykĹ 'adowym problemem optymalizacji, ktĂłry zwykle ma duĹźÄ … iloĹ „Ä ‡ moĺźliwych rozwiÄ … zaĹ”, byĹ ’ by problem traveling salesman. Aby znaleźć rozwiązanie problemu, takiego jak problem podróżującego sprzedawcy, musimy użyć algorytmu, który jest w stanie znaleźć wystarczająco dobre rozwiązanie w rozsądnym czasie. W poprzednim tutorialu przyjrzeliśmy się, jak możemy to zrobić za pomocą algorytmów genetycznych i chociaż algorytmy genetyczne są jednym ze sposobów, w jaki możemy znaleźć „wystarczająco dobre” rozwiązanie problemu podróżującego sprzedawcy, istnieją inne prostsze algorytmy, które możemy wdrożyć, które również znajdą nam bliskie optymalnego rozwiązania. W tym samouczku algorytm, którego będziemy używać, to „symulowane wyżarzanie”.
jeśli nie jesteś zaznajomiony z problemem traveling salesman, może warto rzucić okiem na mój poprzedni tutorial przed kontynuowaniem.
Co To jest symulowane wyżarzanie?
najpierw przyjrzyjmy się, jak działa symulowane wyżarzanie i dlaczego dobrze jest znaleźć rozwiązania problemu podróżującego sprzedawcy. Symulowany algorytm wyżarzania został pierwotnie zainspirowany procesem wyżarzania w obróbce metali. Wyżarzanie polega na ogrzewaniu i chłodzeniu materiału w celu zmiany jego właściwości fizycznych ze względu na zmiany w jego wewnętrznej strukturze. Gdy metal chłodzi, jego nowa struktura staje się stała, co powoduje, że metal zachowuje swoje nowo uzyskane właściwości. W symulowanym wyżarzaniu utrzymujemy zmienną temperaturę, aby symulować ten proces ogrzewania. Początkowo ustawiamy go wysoko, a następnie pozwalamy mu powoli „ostygać” w miarę działania algorytmu. Podczas gdy ta zmienna temperatury jest wysoka, algorytm będzie mógł, z większą częstotliwością, akceptować rozwiązania, które są gorsze niż nasze obecne rozwiązanie. Daje to algorytmowi możliwość wyskoczenia z wszelkich lokalnych optymalizacji, które znajduje na początku wykonania. Ponieważ temperatura jest zmniejszona, więc jest szansa na zaakceptowanie gorszych rozwiązań, co pozwala algorytmowi stopniowo skupiać się na obszarze przestrzeni poszukiwań, w którym, miejmy nadzieję, można znaleźć prawie optymalne rozwiązanie. Ten stopniowy proces „chłodzenia” jest tym, co sprawia, że symulowany algorytm wyżarzania jest niezwykle skuteczny w znalezieniu niemal optymalnego rozwiązania w przypadku dużych problemów, które zawierają liczne lokalne optymalne rozwiązania. Charakter problemu podróżującego sprzedawcy sprawia, że jest to doskonały przykład.
zalety symulowanego wyżarzania
możesz się zastanawiać, czy istnieje jakaś prawdziwa zaleta wdrożenia symulowanego wyżarzania nad czymś w rodzaju prostego wspinacza. Chociaż wspinacze górscy mogą być zaskakująco skuteczni w znalezieniu dobrego rozwiązania, mają również tendencję do utknięcia w lokalnych optimumach. Jak wcześniej ustaliliśmy, symulowany algorytm wyżarzania jest doskonały w unikaniu tego problemu i jest znacznie lepszy średnio w znalezieniu przybliżonego globalnego optimum.
aby lepiej zrozumieć, przyjrzyjmy się szybko, dlaczego podstawowy algorytm wspinaczki górskiej jest tak podatny na wpadanie w lokalne optymalizacje.
algorytm wspinacza górskiego po prostu zaakceptuje rozwiązania sąsiada, które są lepsze od obecnego. Kiedy wspinacz nie może znaleźć lepszych sąsiadów, zatrzymuje się.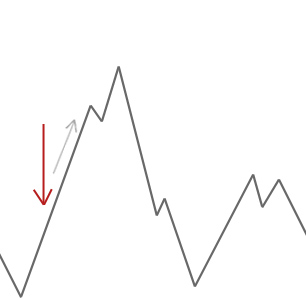
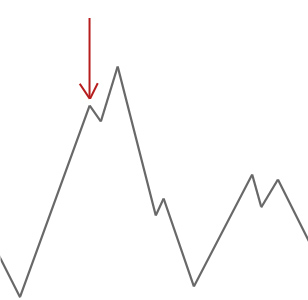
w powyższym przykładzie rozpoczynamy wspinaczkę górską od czerwonej strzałki i działa ona w górę, aż osiągnie punkt, w którym nie może wspiąć się wyżej bez pierwszego zejścia. W tym przykładzie wyraźnie widać, że utknął w lokalnym optimum. Gdyby to był prawdziwy problem, nie wiedzielibyśmy, jak wygląda przestrzeń poszukiwań, więc niestety nie bylibyśmy w stanie stwierdzić, czy to rozwiązanie jest w ogóle zbliżone do globalnego optimum.
Symulowane wyżarzanie działa nieco inaczej niż to i od czasu do czasu akceptuje gorsze rozwiązania. Ta cecha symulowanego wyżarzania pomaga mu wyskoczyć z lokalnych optimum, w których mógłby się utknąć.
funkcja akceptacji
przyjrzyjmy się, w jaki sposób algorytm decyduje, które rozwiązania zaakceptować, abyśmy mogli lepiej zrozumieć, w jaki sposób jest w stanie uniknąć tych lokalnych optymalizacji.
najpierw sprawdzamy, czy rozwiązanie sąsiada jest lepsze od naszego obecnego. Jeśli tak, akceptujemy to bezwarunkowo. Jeśli jednak rozwiązanie sąsiada nie jest lepsze, musimy wziąć pod uwagę kilka czynników. Po pierwsze, o ile gorsze jest rozwiązanie sąsiada, a po drugie, jak wysoka jest obecna „temperatura” naszego systemu. W wysokich temperaturach system częściej przyjmuje rozwiązania, które są gorsze.
matematyka dla tego jest dość prosta:
zasadniczo, im mniejsza zmiana energii (jakość roztworu) i wyższa temperatura, tym bardziej prawdopodobne jest, że algorytm zaakceptuje rozwiązanie.
przegląd algorytmów
więc jak wygląda algorytm? Cóż, w swojej najbardziej podstawowej implementacji jest to dość proste.
- najpierw musimy ustawić temperaturę początkową i utworzyć losowe rozwiązanie początkowe.
- następnie rozpoczynamy zapętlanie, dopóki nasz warunek stop nie zostanie spełniony. Zwykle albo system wystarczająco się ochłodził, albo znaleziono wystarczająco dobre rozwiązanie.
- stąd wybieramy sąsiada, wprowadzając niewielką zmianę w naszym obecnym rozwiązaniu.
- następnie decydujemy, czy przejść do rozwiązania sąsiada.
- w końcu obniżamy temperaturę i kontynuujemy zapętlanie
Inicjalizacja temperatury
dla lepszej optymalizacji, inicjując zmienną temperaturową powinniśmy wybrać temperaturę, która początkowo pozwoli na praktycznie każdy ruch w stosunku do obecnego rozwiązania. Daje to algorytmowi możliwość lepszego zbadania całej przestrzeni wyszukiwania przed ochłodzeniem i osadzeniem się w bardziej skoncentrowanym regionie.
przykładowy kod
teraz użyjmy tego, co wiemy, aby utworzyć podstawowy symulowany algorytm wyżarzania, a następnie zastosować go do problemu podróżującego sprzedawcy poniżej. Będziemy używać Javy w tym samouczku, ale logika powinna być na tyle prosta, aby skopiować ją do dowolnego wybranego języka.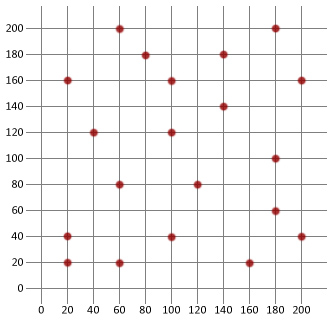
najpierw musimy stworzyć klasę miejską, która może być używana do modelowania różnych miejsc docelowych naszego podróżującego sprzedawcy.
miasto.java
* miasto.java
* Models A city
*/
package sa;
public class City {
int x;
int y;
/ / tworzy losowo umieszczone miasto
public City () {
this.x = (int) (Math.random ()*200);
this.y = (int) (Math.losowe()*200);
}
// konstruuje miasto w wybranym miejscu x, y
public City (int x, int y){
this.x = x;
to.y = y;
}
// pobiera współrzędną X miasta
public int getX () {
zwraca to.x;
}
// pobiera współrzędną Y miasta
public int getY () {
zwraca to.y;
}
// pobiera odległość do podanego miasta
public double distanceTo(City city) {
int xDistance = Math.abs (getX () – miasto.getX());
int yDistance = Math.abs (getY () – miasto.getY ());
double distance = Math.sqrt ((xDistance*xDistance) + (yDistance*yDistance) );
return distance;
}
@Override
public String toString () {
return getX ()+”, ” + getY();
}
}
następnie stwórzmy klasę, która może śledzić miasta.
TourManager.java
* TourManager.java
* przechowuje miasta wycieczki
*/
pakiet sa;
import java.util.ArrayList;
public class TourManager {
/ / posiada nasze miasta
private static ArrayList destinationCities = new ArrayList < City>();
// dodaje miasto docelowe
public static void addCity(City city) {
destinationCities.add (miasto);
}
// Get a city
public static City getCity(int index) {
return (City)destinationCities.get (indeks);
}
// Pobierz liczbę miast docelowych
public static int numberOfCities () {
return destinationCities.rozmiar();
}
}
teraz, aby stworzyć klasę, która może modelować podróżującego sprzedawcę.
wycieczka.java
* Tour.java
* przechowuje wycieczkę kandydata PO wszystkich miastach
*/
pakiet sa;
Importuj Javę.util.ArrayList;
Importuj Javę.util.Kolekcje;
wycieczka po klasie publicznej {
/ / prowadzi naszą wycieczkę po miastach
prywatna wycieczka po liście obiektów = nowa lista obiektów< miasto>();
// Pamięć podręczna
private int distance = 0;
/ / tworzy pustą wycieczkę
wycieczka publiczna () {
dla (int i = 0; i < menedżer wycieczek.numberOfCities (); i++) {
.add (null);
}
}
// konstruuje trasę z innej trasy
public Tour(ArrayList tour) {
this.tour = (ArrayList) tour.klon();
}
// Returns tour information
public ArrayList getTour(){
return tour;
}
// tworzy losową jednostkę
Public void generateIndividual () {
/ / Pętla przez wszystkie nasze miasta docelowe i dodać je do naszej wycieczki
for (int cityIndex = 0; Cityindex < TourManager.numberOfCities (); cityIndex++) {
setCity (cityIndex, TourManager.getCity (cityIndex));
}
// losowo Zmień kolejność kolekcji tour
.shuffle (trasa);
}
// dostaje miasto z wycieczki
publiczne miasto getCity(int tourPosition) {
powrót (miasto)wycieczka.get (tourPosition);
}
// Ustawia miasto w określonej pozycji w trasie
Public void setCity(int tourPosition, City city) {
tour.set (tourPosition, city);
/ / jeśli trasy zostały zmienione musimy zresetować kondycję i odległość
odległość = 0;
}
// pobiera całkowity dystans wycieczki
public int getDistance () {
if (distance = = 0) {
int tourDistance = 0;
/ / pętla po miastach naszej wycieczki
for (int cityIndex=0; cityIndex < tourSize(); cityindex++) {
// Get city podróżujemy z
City fromCity = getCity(cityIndex);
// City podróżujemy do
city destinationCity;
// sprawdź, czy nie jesteśmy na ostatnim mieście naszej wycieczki, jeśli ustawiliśmy nasze
// miasto docelowe wycieczki do naszego miasta początkowego
if(cityindex+1 < toursize()){
destinationcity = getcity(cityindex+1);
}
else{
destinationCity = getCity(0);
}
// uzyskaj odległość między dwoma miastami
tourDistance + = fromCity.distanceTo (destinationCity);
}
distance = tourDistance;
}
odległość powrotu;
}
// uzyskaj liczbę miast na naszej trasie
public int tourSize () {
return tour.rozmiar();
}
@Override
public String toString () {
String geneString = „|”;
for (int i = 0; i < tourSize(); i++) {
geneString += getCity(i)+”|”;
}
return geneString;
}
}
na koniec stwórzmy nasz symulowany algorytm wyżarzania.
Symulacja.java
public class SimulatedAnnealing {
/ / Oblicz prawdopodobieństwo akceptacji
public static double acceptanceProbability(int energy, int newEnergy, double temperature) {
// jeśli nowe rozwiązanie jest lepsze, zaakceptuj je
if (newEnergy < energy) {
return 1.0;
}
// jeśli nowe rozwiązanie jest gorsze, Oblicz prawdopodobieństwo akceptacji
return Math.exp ((energia – newEnergy) / temperatura);
}
public static void main (String args) {
// Utwórz i dodaj nasze miasta
City city = new City(60, 200);
TourManager.addCity (miasto);
City city2 = new City(180, 200);
TourManager.addCity(city2);
City city3 = new City (80, 180);
TourManager.addCity (city3);
City city4 = new City (140, 180);
TourManager.addCity (city4);
City city5 = new City (20, 160);
TourManager.addCity (city5);
City city6 = new City(100, 160);
TourManager.addCity (city6);
City city7 = new City (200, 160);
TourManager.addCity (city7);
City city8 = new City (140, 140);
TourManager.addCity (city8);
City city9 = new City (40, 120);
TourManager.addCity (city9);
City city10 = new City(100, 120);
TourManager.addCity (city10);
City city11 = new City (180, 100);
TourManager.addCity (city11);
City city12 = new City (60, 80);
TourManager.addCity (city12);
City city13 = new City (120, 80);
TourManager.addCity (city13);
City city14 = new City (180, 60);
TourManager.addCity (city14);
City city15 = new City (20, 40);
TourManager.addCity (city15);
City city16 = new City (100, 40);
TourManager.addCity (city16);
City city17 = new City (200, 40);
TourManager.addCity (city17);
City city18 = new City(20, 20);
TourManager.addCity (city18);
City city19 = new City (60, 20);
TourManager.addCity (city19);
City city20 = new City (160, 20);
TourManager.addCity (city20);
// Set initial temp
double temp = 10000;
// cooling rate
double coolingRate = 0.003;
// Initialize intial solution
tour currentSolution = new Tour ();
currentSolution.generateIndividual ();
System.Wynocha.println („Initial solution distance:” + currentSolution.getDistance());
// Ustaw jako current best
Tour best = new Tour(currentSolution.getTour());
// Loop until system has cooled
while (temp > 1) {
// Create new neighbour tour
Tour newSolution = new Tour(currentSolution.getTour ());
// uzyskaj losową pozycję w trasie
int tourPos1 = (int) (newSolution.tourSize () * Math.random ());
int tourPos2 = (int) (newSolution.tourSize () * Math.random ());
/ / Get the cities at selected positions in the tour
City citySwap1 = newSolution.getCity (tourPos1);
City citySwap2 = newSolution.getCity (tourPos2);
/ / zamień je
.setCity (tourPos2, citySwap1);
newSolution.setCity (tourPos1, citySwap2);
// uzyskaj energię rozwiązań
int currentEnergy = currentSolution.getDistance ();
Intel = newSolution . getDistance();
// zdecyduj, czy powinniśmy zaakceptować sąsiada
jeśli (acceptanceProbability (currentEnergy, neighbourEnergy, temp) >.random ()) {
currentSolution = new Tour (newSolution.getTour());
}
// śledź najlepsze znalezione rozwiązanie
if (currentSolution.getDistance () < best.getDistance ()) {
best = new Tour (currentSolution.getTour());
}
// Cool system
temp *= 1-coolingRate;
}
System.Wynocha.println („Final solution distance:” + best.getDistance ());
System.Wynocha.println („Tour:” + best);
}
}
wyjście
końcowa odległość rozwiązania: 911
wycieczka: |180, 200/200, 160/140, 140/180, 100/180, 60/200, 40/160, 20/120, 80/100, 40/60, 20/20, 20/20, 40/60, 80/100, 120/40, 120/20, 160/60, 200/80, 180/100, 160/140, 180|
wniosek
w tym przykładzie byliśmy w stanie uzyskać więcej niż połowę odległości naszej początkowej losowo wygenerowanej trasy. To, miejmy nadzieję, pokazuje, jak przydatny jest ten stosunkowo prosty algorytm, gdy jest stosowany do niektórych rodzajów problemów optymalizacyjnych.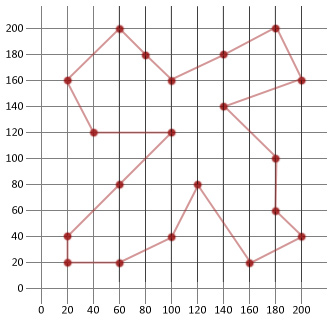
Autor
 Witam, jestem Lee.
Witam, jestem Lee.jestem programistą z Wielkiej Brytanii, który kocha technologię i biznes. Tutaj znajdziesz artykuły i tutoriale na temat rzeczy, które mnie interesują. Jeśli chcesz mnie zatrudnić lub dowiedzieć się więcej o mnie wejdź na moją stronę O mnie