Nota wydawcy: Tony Abbey prowadzi zajęcia NAFEMS na żywo w USA, Europie i Azji. Prowadzi również zajęcia e-learningowe NAFEMS na całym świecie. Kontakt .po szczegóły.
poprzedni artykuł inżynierski („Uprość modele symulacji mes przy użyciu symetrii planarnej”) wyjaśnił, że nawet w przypadku potężnych nowoczesnych komputerów często istnieje motywacja do stosowania technik upraszczania w strukturalnej analizie elementów skończonych (FEA). Ta kontynuacja opisuje, w jaki sposób dwie ściśle powiązane metody mogą być stosowane do pobierania plastrów 2D przez złożoną strukturę w regionach zainteresowania. Uzyskane modele mes mogą dać cenny wgląd w lokalne naprężenia szybciej i skuteczniej niż pełny model 3D. Nie opowiedzą całej historii, ale są cennymi narzędziami dla inżyniera CAE.
dwie metody FEA nazywane są naprężeniem płaszczyznowym i odkształceniem płaszczyznowym. Oba używają płaskich elementów 2D, które wyglądają jak cienkie elementy powłoki i są zazębione za pomocą płaskiej geometrii powierzchni.
Analiza Naprężeń Płaszczyzny
Rys. 1 pokazuje ważne fakty dotyczące analizy naprężeń płaszczyzny. Zakłada się, że obszar strukturalny leży w płaszczyźnie 2D xy, przy czym trzeci wymiar strukturalny jest stosunkowo niewielki. Na rysunku jest to grubość w kierunku Z. Naprężenia istnieją w płaszczyźnie 2D jako sigma x, sigma y (naprężenia bezpośrednie) i sigma xy (naprężenia ścinające w płaszczyźnie). Każde z tych naprężeń jest stałe przez grubość, jak pokazano we wstawce. Ponadto nie może być stresu w kierunku Z. Ta zależność materiałowa naprężenie-odkształcenie jest zdefiniowana w elementach naprężeń płaszczyzny 2D stosowanych w tego typu analizie.
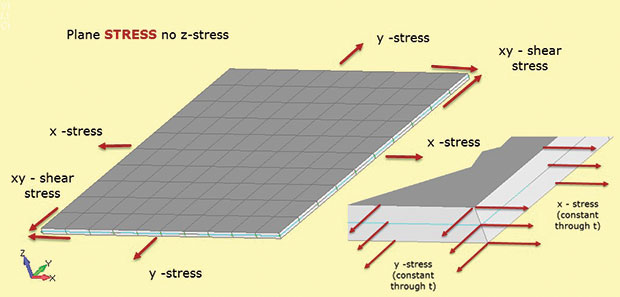rys. 1: stres płaszczyzny; założenia stanu stresu.brak naprężenia z jest sposobem na zapamiętanie naprężenia płaszczyzny oznaczenia typu elementu (tzn. dozwolone są tylko naprężenia w płaszczyźnie). Nie ma również naprężeń ścinających przez grubość. Możemy załadować model naprężenia płaszczyzny na Rys. 1 z obciążeniem dwuosiowym i obliczyć sigma x i sigma y. nie ma sigma z. możemy również obliczyć odpowiednie naprężenia w płaszczyźnie e-x i e-y. jeśli zastosujemy obciążenie ścinające, możemy znaleźć naprężenie ścinające sigma xy i naprężenie ścinające e-xy. Co ciekawe, możemy również obliczyć odkształcenie grubości przelotowej e-z. to nie jest zero, ponieważ model może swobodnie zmniejszać się w z, gdy rozciąga się w x i Y. nie ma ograniczeń poza płaszczyzną, aby temu zapobiec. W niektórych rozwiązaniach możemy odzyskać odkształcenie grubości przelotowej e-z i użyć go do obliczenia zmiany grubości. (Jeśli model jest w kompresji dwuosiowej, wtedy sekcja z będzie grubsza). Jest to zwykle uważane za odkształcenie wtórne i może nie być dostępne na wyjściu-ale istnieje i może być obliczone ręcznie w razie potrzeby.
2 pokazuje aluminiowy element końcówki. Końcówka wystaje z kompozytowego układu arkusza, który ma warstwy umieszczone i połączone nad trzpieniami (lub nogami) i dolną częścią ciała. Trzpienie przenoszą obciążenie przyłożone do końcówki w strukturę kompozytową. W praktyce warstwy byłyby stopniowane, aby umożliwić płynne przenoszenie ścinania przez wiązanie do kompozytu. Przeniesienie ścinania do kompozytu jest tutaj symulowane przez rozproszone siły trakcyjne powierzchni „ciągnące” na stygi. Równoważą one przyłożone obciążenie lug.
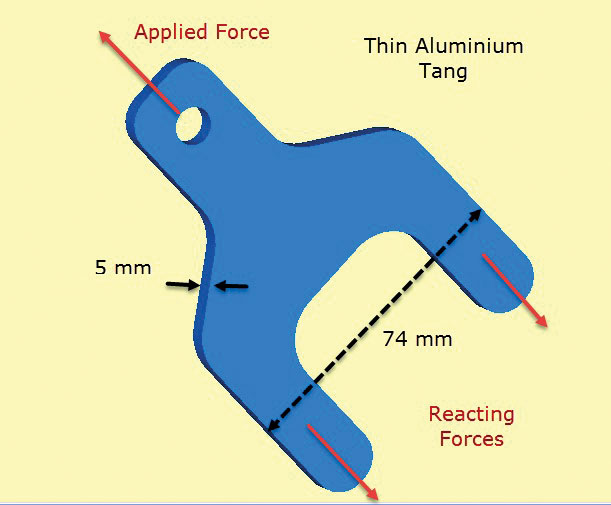rys. 2: Cienkościenny trzpień aluminiowy przenoszący obciążenie na strukturę kompozytową.kluczowym założeniem jest to, że naprężenia przez grubość są zerowe, a naprężenia w płaszczyźnie są stałe przez grubość elementu. Oznacza to, że lokalny szczegół przeniesienia obciążenia ścinającego z kompozytu na trzpień jest słabo modelowany. Jednak celem tej analizy jest sprawdzenie rozmiaru przekroju końcówki i trzpienia bez kompozytu, przy użyciu naprężeń płaskich.
grubość elementu jest niewielka w porównaniu do innych wymiarów. Wartość ta jest wprowadzana jako rzeczywista grubość w definicji elementu naprężenia płaszczyzny.
3 pokazuje model MES i obliczone maksymalne naprężenia główne. Obszary zainteresowania są wokół łap i promieni barkowych. W świecie rzeczywistym stan naprężeń przy stężeniach naprężeń byłby trójwymiarowy, a poprzez grubość naprężenia sigma Z i naprężenia ścinające równoważyłyby się lokalnie. Jednak bardzo rozsądne jest założenie, że dominują naprężenia w płaszczyźnie. Jest to to samo założenie ukryte w większości tradycyjnych obliczeń koncentracji naprężeń (Kt) znalezionych w podręcznikach.
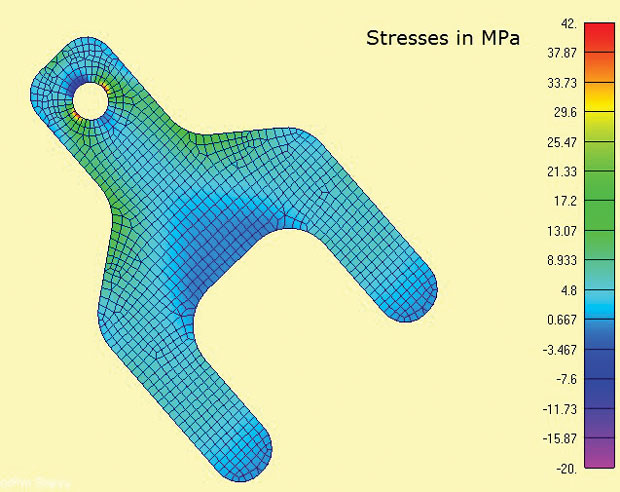ryc. 3: elementy naprężenia płaszczyzny 2D pokazujące maksymalne naprężenia główne jedną z wygodnych cech analizy naprężeń płaszczyzny jest to, że jest to analiza ściśle 2D, więc tylko trzy stopnie swobody (DOF) muszą być ograniczone (w płaszczyźnie tłumaczenia x, y i obrót wokół osi z). Nadaje się to do metody minimalnego ograniczenia 3-2-1 z zrównoważonym obciążeniem. W przypadku 2D ta degeneruje się do metody 2-1. Jeden węzeł ma ograniczone DOF x i y, drugi odpowiedni węzeł ortogonalny ma ograniczone DOF x. Pozwala to na przykład obciążenie reakcyjne w tangach bezpośrednio jako rozproszone obciążenia równoważące. Trudno byłoby symulować ten warunek graniczny poprzez ograniczenia do ziemi.
przelotowe odkształcenie e-z, a tym samym rozrzedzenie Tangów, można obliczyć jako efekt wtórny.
Analiza Odkształceń Płaszczyzny
Rys. 4 pokazuje istotę metody odkształcenia płaszczyznowego. Ponownie stosuje się elementy planarne 2D, ale z subtelnie odmiennymi założeniami. Naprężenia płaszczyznowe x, y i xy rozwijają się jak poprzednio. Jednak tym razem jest to poza płaszczyzną, lub przez odkształcenie grubości z, które jest ustawione na zero. Tak więc analiza szczepów płaszczyznowych pozwala tylko na szczepy w płaszczyźnie. Działa to dobrze, aby reprezentować grube struktury, takie jak pokazano. Obecność tego materiału ma tendencję do stabilizacji komponentu i zapobiegania jego naprężeniu w z.Oznacza to również, że w konstrukcji powstają stałe naprężenia o grubości Z. Ta zależność materiałowa naprężenie-odkształcenie jest zdefiniowana w elementach odkształcenia płaszczyzny 2D stosowanych w tego typu analizie.
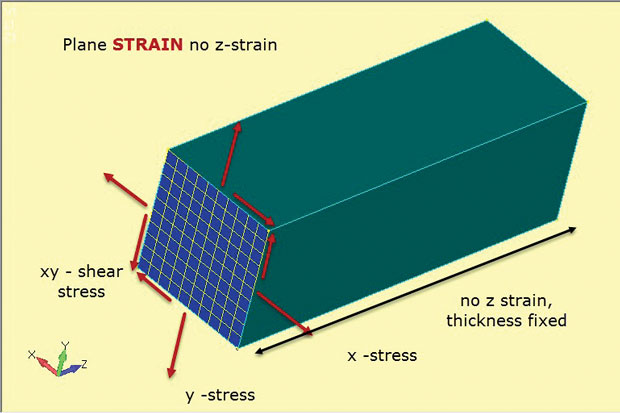rys. 4: Analiza odkształceń płaszczyzny; założenia dotyczące stanu naprężeń i odkształceń.rysunek przedstawia orientację płaszczyzn dwuwymiarowych jako przekrój przecięty przez typowy element głęboki. Zakłada się, że stan naprężenia na tym ciętym odcinku będzie duplikowany na dowolnym przecięciu płaszczyzny xy (stacji z) przez komponent. Zakłada się, że element jest pryzmatyczny (o stałym przekroju) na całej swojej długości.
w praktyce używamy tej metody, gdzie stan naprężenia zmienia się powoli z płaszczyzny na płaszczyznę w głębokim elemencie. Powinno być wystarczająco dużo materiału przez głębokość, aby ustabilizować i wyeliminować odkształcenie grubości przelotowej. Jest to ta sama zasada stosowana w próbkach odporności na pękanie pokazanych na Fig. 5. Uszkodzenie w Warunkach odkształcenia płaszczyzny jest pokazane dla środkowej części grubej próbki. Awaria na wolnych krawędziach i cienkiej sekcji to inny tryb, bardziej jak stan naprężenia płaszczyzny. Płaszczyznowy model szczepu FEA byłby z definicji dobrym odzwierciedleniem zachowania grubej próbki w linii środkowej, ale nie wolnych krawędzi lub cienkiej próbki.
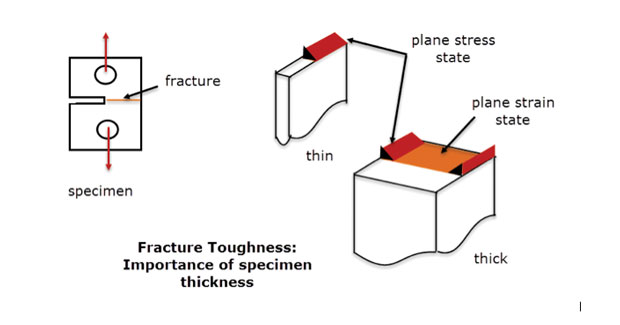rys. 5: próbki odporności na pękanie; cienkie i grube sekcje.6 pokazuje inny komponent stosowany w strukturze kompozytowej, tworząc złącze. Tutaj sekcja jest stała i na tyle głęboka, że możemy założyć, że naprężenia są również stałe z głębokością. Swobodne powierzchnie końcowe (przy + z, – z) będą miały inny lokalny stan naprężenia (właściwie naprężenie płaszczyznowe, jak zauważono), jednak celem tej analizy jest sprawdzenie naprężeń sekcji netto na linii środkowej (z = 0).
siatka do analizy odkształceń płaszczyzny 2D jest pokazana w części 3D na Fig. 7. Wycinek odcinka jest zdefiniowany na stacji z = 0.
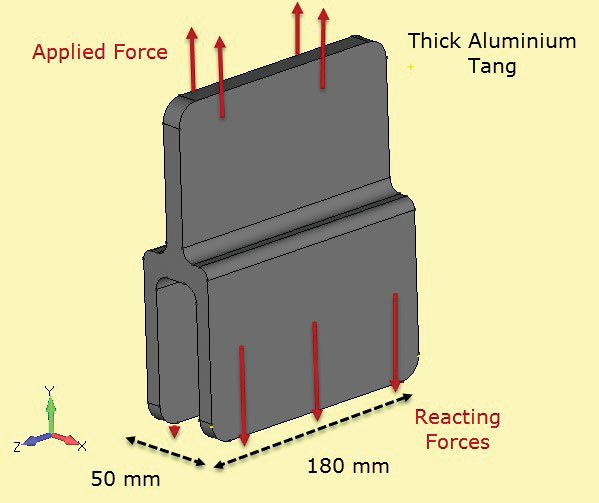rys. 6: trzpień aluminiowy o głębokim przekroju.
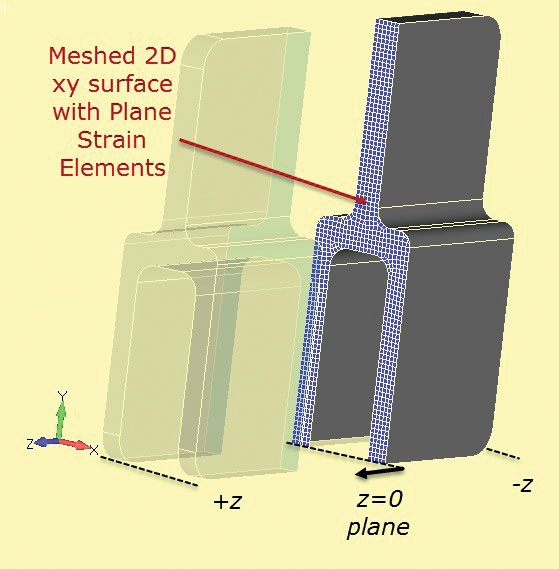rys. 7: Sekcja przecięta przez solidną sekcję, aby rozwinąć sekcję odkształcenia płaszczyzny 2D.można zastosować bardzo drobną siatkę odkształcającą 2D, która będzie działać bardzo szybko w porównaniu do pełnego modelu 3D. Metoda 2-1 jest używana jak poprzednio. Załadunek musi być starannie przemyślany. „Grubość” sekcji naprężenia płaszczyzny jest dość Dowolna i zwykle domyślnie ustawiana jest na 1.0. Jeśli obciążenie komponentu jest obliczane jako obciążenie robocze przez głębokość (N / m, Lbf / cal itp.) wtedy wartość ta może być użyta bezpośrednio na płaskiej siatce odkształcającej. Przydatne jest wybranie sekcji, takiej jak pojedynczy tang i oszacowanie nominalnego lub średniego naprężenia w tej sekcji dla pełnego składnika. Może to być wykorzystane jako kontrola poczytalności w analizie odkształceń płaszczyzny. Nieprawidłowe ładowanie jest prawdopodobnie główną przyczyną błędu w tej metodzie.
wyniki analizy przedstawiono na Fig. 8 i pokaż wyraźnie obszary dużego stresu wokół filetu barkowego. Naprężenia są ważne dla centralnego obszaru głębokości elementu (z = 0).
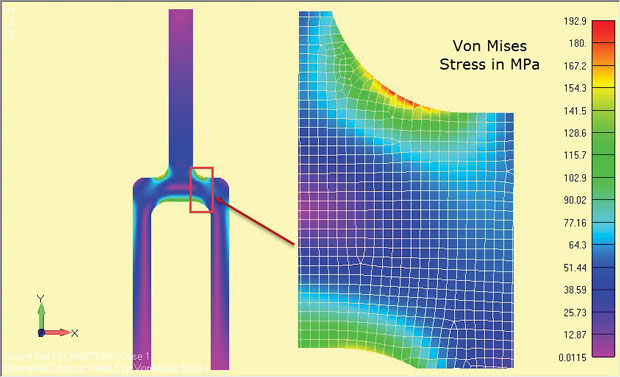rys. 8: Wyniki analizy odkształceń płaszczyzny elementu głębokiego tang.zastosowane ilości naprężeń zależą od zastosowanego solvera. Niektóre rozwiązania ignorują naprężenia kierunku z jako wtórne i odzyskują naprężenia w płaszczyźnie. Naprężenia główne i naprężenia von Misesa odnoszą się następnie do stanu naprężenia w płaszczyźnie 2D. Jeśli naprężenie kierunku z jest odzyskiwane, należy je wyraźnie zidentyfikować,aby można było zidentyfikować stan naprężenia płaszczyzny 2D w płaszczyźnie x-Y.
co dokładnie oznacza naprężenie kierunku z? Jest to naprężenie opracowane w wyniku wymuszenia odkształcenia kierunku zerowego Z. Naprężenie działa tak, jakby wolne powierzchnie czołowe sekcji pryzmatycznej były zamocowane. Na centralnej płaszczyźnie elementu głębokiego przekroju będą to naprężenia uzupełniające potrzebne do utrzymania stanu naprężenia kierunku zero Z. W rzeczywistości, gdy poruszamy się w kierunku swobodnych powierzchni, naprężenie z spada do zera i staje się rozkładem naprężeń płaskich (jak widać w próbce mechaniki grubego pękania).
w wielu przypadkach, takich jak cylinder pod ciśnieniem, powierzchnie czołowe są ograniczone i w rzeczywistości rozwijają się naprężenia osiowe z powodu sił osiowych. Będzie to naprężenie inne niż naprężenie osiowe indukowane w analizie odkształceń płaszczyzny. Do obliczenia naprężeń osiowych konieczne będzie obliczenie ręczne lub ewentualnie dodatkowy model osiowo-symetryczny dla zbiorników ciśnieniowych.
łatwość geometrii i konstrukcji siatki nadaje się dobrze do badań „co-jeśli” lub bardziej formalnych badań optymalizacji kształtu.
dla porównania wykonano pełną analizę 3D składowej tang głębokiego o symetrii połówkowej, a wyniki przedstawiono na Fig. 9. Nominalne naprężenie na górnej pojedynczej nodze jest identyczne w obu przypadkach-pamiętaj, że jest to podstawa każdej kontroli zdrowia psychicznego.
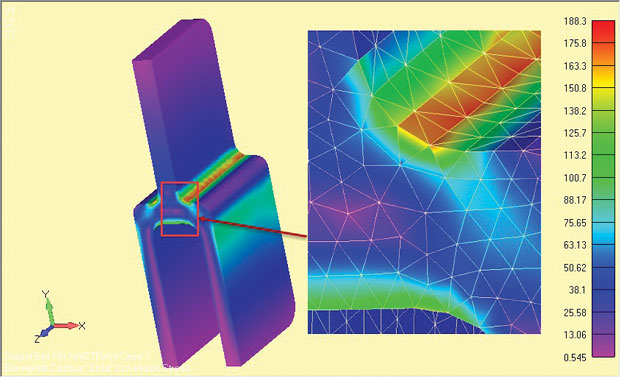rys. 9: Pełny model 3D głębokiego tanga, pokazujący wyniki stresu.lokalne naprężenia barku są niższe o niewielki procent w pełnym modelu. Jest to z trzech powodów. Po pierwsze, stosunkowo gruba siatka tet 3D jest gorsza od bardzo drobnej lokalnej siatki 2D. Nie przeprowadzono kontroli zbieżności modelu 3D.
po drugie, na powierzchniach swobodnych (+z, -z) występuje niewielka zmiana geometrii w porównaniu z sekcją z = 0 ze względu na końcówki. W tym przypadku efekt jest znikomy, ponieważ filety są z dala od regionów barkowych. W wielu komponentach będą jednak lokalne filety i zabraknie szczegółów. które będą się różnić geometrią od prostej płaszczyzny XY. Lokalne zmiany naprężeń na wolnych powierzchniach końcowych mogą wymagać oszacowania lub sprawdzenia za pomocą pełnego modelu 3D.
wreszcie, założenie odkształcenia płaszczyzny stałego ograniczenia z w sekcjach +z,-Z nie jest prawdziwe dla skończonej składowej głębokości. Naprężenie z rozproszy się do zera na” prawdziwych ” wolnych twarzach. Efekt ten pokazano na Fig. 10, który wykorzystuje model 3D, jak jest, a także jako symulację naprężenia odkształcenia płaszczyzny Z.
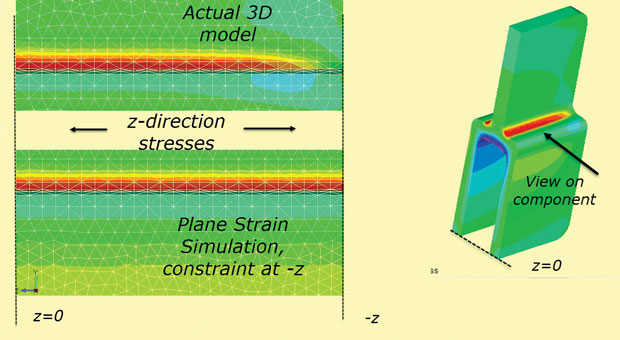rys. 10: Dyfuzja naprężenia z w kierunku wolnej powierzchni.szybkie i wydajne
analizy naprężeń i odkształceń płaszczyzny są przydatnymi metodami 2D, które często mogą uzupełniać pełnowymiarowe modele 3D. Nie wszystkie funkcje mogą być reprezentowane, ale przy pewnej pomysłowości można przynajmniej oszacować naprężenia w kluczowych obszarach. Motywacją do stosowania tych metod jest umożliwienie szybkiej, efektywnej analizy z łatwą geometrią 2D i konstrukcją siatki.