Algoritm Greedy cu exemple: metoda Greedy & abordare

pentru a înțelege abordarea lacomă, va trebui să aveți o cunoaștere de lucru a recursivității și a comutării contextului. Acest lucru vă ajută să înțelegeți cum să urmăriți codul. Puteți defini paradigma lacomă în termenii propriilor declarații necesare și suficiente.

două condiții definesc paradigma lacomă.

• fiecare soluție în trepte trebuie să structureze o problemă către soluția cea mai bine acceptată.
• este suficient dacă structurarea problemei se poate opri într-un număr finit de pași lacomi.

cu teoretizarea continuată, să descriem istoria asociată cu abordarea de căutare lacomă.

în acest tutorial algoritm Greedy, veți învăța:

• istoria algoritmilor Greedy
• strategii și decizii Greedy
• caracteristicile abordării Greedy
• de ce să folosiți abordarea Greedy?
• cum se rezolvă problema selecției activității
• arhitectura abordării Greedy
• dezavantajele algoritmilor Greedy

istoria algoritmilor Greedy

Iată un reper important al algoritmilor greedy:

• algoritmii Greedy au fost conceptualizați pentru mulți algoritmi de mers pe jos în anii 1950.
• Esdger Djikstra a conceptualizat algoritmul pentru a genera copaci minimali. El și-a propus să scurteze durata rutelor din capitala olandeză, Amsterdam.
• în același deceniu, Prim și Kruskal au realizat strategii de optimizare care s-au bazat pe minimizarea costurilor traseului de-a lungul rutelor cântărite.
• în anii ‘ 70, cercetătorii americani, Cormen, Rivest și Stein au propus o substructurare recursivă a soluțiilor lacome în cartea lor clasică introducere în algoritmi.
• paradigma căutării Greedy a fost înregistrată ca un alt tip de strategie de optimizare în înregistrările NIST în 2005.
• până în prezent, protocoalele care rulează web-ul, cum ar fi Open-shortest-path-first (OSPF) și multe alte protocoale de comutare a pachetelor de rețea utilizează strategia greedy pentru a minimiza timpul petrecut într-o rețea.

strategii și decizii lacome

logica în forma sa cea mai ușoară a fost redusă la „lacom” sau „nu lacom”. Aceste afirmații au fost definite de abordarea adoptată pentru a avansa în fiecare etapă a algoritmului.

de exemplu, algoritmul lui Djikstra a folosit o strategie lacomă în trepte de identificare a gazdelor pe Internet prin calcularea unei funcții de cost. Valoarea returnată de funcția cost a determinat dacă următoarea cale este „greedy” sau „non-greedy”.

pe scurt, un algoritm încetează să mai fie lacom dacă în orice etapă face un pas care nu este lacom local. Problemele lacome se opresc fără alte domenii de lăcomie.

caracteristicile abordării Greedy

caracteristicile importante ale unui algoritm de metodă Greedy sunt:

• există o listă ordonată de resurse, cu costuri sau atribuții de valoare. Acestea cuantifică constrângerile asupra unui sistem.
• veți lua cantitatea maximă de resurse în momentul în care se aplică o constrângere.
• de exemplu, într-o problemă de planificare activitate, costurile de resurse sunt în ore, iar activitățile trebuie să fie efectuate în ordine de serie.

de ce să folosim abordarea lacomă?

iată motivele pentru care se folosește abordarea greedy:

• abordarea lacomă are câteva compromisuri, ceea ce o poate face potrivită pentru optimizare.
• un motiv important este de a obține soluția cea mai fezabilă imediat. În problema de selecție a activității (explicată mai jos), dacă se pot face mai multe activități înainte de finalizarea activității curente, aceste activități pot fi efectuate în același timp.
• un alt motiv este împărțirea recursivă a unei probleme pe baza unei condiții, fără a fi nevoie să combinați toate soluțiile.
• în problema de selecție a activității, pasul „diviziune recursivă” se realizează prin scanarea unei liste de elemente o singură dată și luând în considerare anumite activități.

cum se rezolvă problema de selecție a activității

în exemplul de planificare a activității, există un timp „start” și „finish” pentru fiecare activitate. Fiecare activitate este indexată cu un număr de referință. Există două categorii de activități.

1. activitate considerată: este activitatea, care este referința din care este analizată capacitatea de a face mai multe activități rămase.
2. activități rămase: activități la unul sau mai mulți indici înaintea activității avute în vedere.

durata totală indică costul desfășurării activității. Aceasta este (finish – start) ne dă durational ca costul unei activități.

veți afla că măsura lacomă este numărul de activități rămase pe care le puteți efectua în timpul unei activități considerate.

arhitectura abordării Greedy

pasul 1)

scanați lista costurilor de activitate, începând cu indicele 0 ca indice considerat.

pasul 2)

când mai multe activități pot fi terminate până la momentul respectiv, activitatea considerată se termină, începeți să căutați una sau mai multe activități rămase.

Pasul 3)

dacă nu mai există activități rămase, activitatea rămasă curentă devine următoarea activitate considerată. Repetați pasul 1 și pasul 2, cu noua activitate considerată. Dacă nu mai există activități rămase, treceți la Pasul 4.

pasul 4)

returnați Uniunea indicilor considerați. Acestea sunt indicii de activitate care vor fi utilizați pentru a maximiza randamentul.

explicație Cod

#include<iostream>#include<stdio.h>#include<stdlib.h>#define MAX_ACTIVITIES 12

explicarea codului:

1. inclus fișiere antet / clase
2. un număr maxim de activități furnizate de utilizator.

using namespace std;class TIME{ public: int hours; public: TIME() { hours = 0; }};

explicarea codului:

1. spațiul de nume pentru operațiunile de streaming.
2. o definiție de clasă pentru timp
3. o oră timestamp.
4. un constructor implicit de timp
5. variabila ore.

class Activity{ public: int index; TIME start; TIME finish; public: Activity() { start = finish = TIME(); }};

explicarea codului:

1. o definiție de clasă de activitate
2. Timestamps definirea unei durate
3. toate timestamps sunt inițializate la 0 în constructorul implicit

class Scheduler{ public: int considered_index,init_index; Activity *current_activities = new Activity; Activity *scheduled;

explicarea codului:

1. Partea 1 a definiției clasei scheduler.
2. indexul considerat este punctul de plecare pentru scanarea matricei.
3. indicele de inițializare este utilizat pentru a atribui marcaje temporale aleatorii.
4. o serie de obiecte de activitate este alocată dinamic folosind noul operator.
5. indicatorul programat definește locația de bază curentă pentru lăcomie.

Scheduler(){ considered_index = 0; scheduled = NULL;......

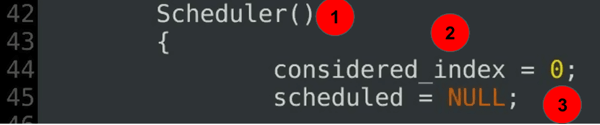
explicarea codului:

1. scheduler constructor-partea 2 a definiției clasei scheduler.
2. indexul considerat definește începutul curent al scanării curente.
3. măsura lacomă actuală este nedefinită la început.

for(init_index = 0; init_index < MAX_ACTIVITIES; init_index++) { current_activities.start.hours = rand() % 12; current_activities.finish.hours = current_activities.start.hours + (rand() % 2); printf("\nSTART:%d END %d\n", current_activities.start.hours ,current_activities.finish.hours); }……

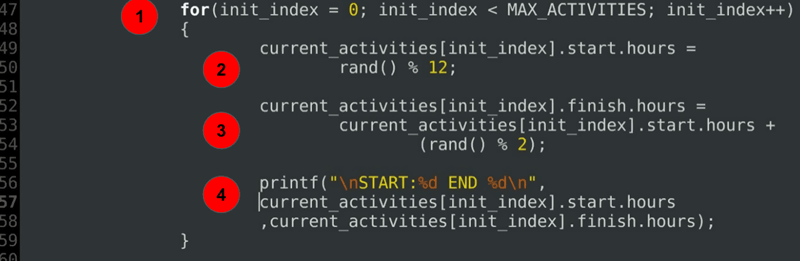
explicarea codului:

1. a Pentru Buclă pentru a inițializa orele de început și orele de sfârșit ale fiecărei activități programate în prezent.
2. inițializarea timpului de pornire.
3. inițializarea timpului de încheiere întotdeauna după sau Exact la ora de începere.
4. o declarație de depanare pentru a imprima durate alocate.

public: Activity * activity_select(int);};

explicarea codului:

1. Partea 4 – ultima parte a definiției clasei planificator.
2. activitate selectați funcția ia un indice punct de plecare ca bază și împarte căutarea greedy în subprobleme greedy.

Activity * Scheduler :: activity_select(int considered_index){ this->considered_index = considered_index; int greedy_extent = this->considered_index + 1;…… 

1. folosind operatorul de rezoluție a domeniului (::), este furnizată definiția funcției.
2. indicele considerat este indicele numit prin valoare. Greedy_extent este inițializat doar un index după Indicele considerat.

Activity * Scheduler :: activity_select(int considered_index){ while( (greedy_extent < MAX_ACTIVITIES ) && ((this->current_activities).start.hours < (this->current_activities).finish.hours )) { printf("\nSchedule start:%d \nfinish%d\n activity:%d\n", (this->current_activities).start.hours, (this->current_activities).finish.hours, greedy_extent + 1); greedy_extent++; }…...

explicarea codului:

1. logica de bază – gradul lacom este limitat la numărul de activități.
2. orele de început ale activității curente sunt verificate ca programabile înainte ca activitatea considerată (dată de indexul considerat) să se termine.
3. atâta timp cât este posibil, se imprimă o instrucțiune de depanare opțională.
4. treceți la următorul index din matricea de activități

...if ( greedy_extent <= MAX_ACTIVITIES ) { return activity_select(greedy_extent); } else { return NULL; }}

explicarea codului:

1. verificările condiționate dacă toate activitățile au fost acoperite.
2. dacă nu, puteți reporni greedy cu indexul considerat ca punct curent. Acesta este un pas recursiv care împarte cu lăcomie afirmația problemei.
3. dacă da, se întoarce la apelantul cu nici o posibilitate de extindere lăcomie.

int main(){ Scheduler *activity_sched = new Scheduler(); activity_sched->scheduled = activity_sched->activity_select( activity_sched->considered_index); return 0;}

explicarea codului:

1. funcția principală utilizată pentru a invoca Planificatorul.
2. un nou planificator este instanțiat.
3. funcția de selectare a activității, care returnează un pointer de activitate de tip, revine apelantului după terminarea căutării greedy.

ieșire:

START:7 END 7START:9 END 10START:5 END 6START:10 END 10START:9 END 10Schedule start:5 finish6 activity:3Schedule start:9 finish10 activity:5

dezavantaje ale algoritmilor Greedy

nu este potrivit pentru problemele Greedy în care este necesară o soluție pentru fiecare subproblemă, cum ar fi sortarea.

în astfel de probleme de practică algoritm Greedy, metoda Greedy poate fi greșit, în cel mai rău caz, chiar duce la o soluție non-optimă.

prin urmare, dezavantajul algoritmilor greedy este folosirea neștiind ce se află în fața stării greedy actuale.

mai jos este o descriere a dezavantajului metodei Greedy:

în scanarea greedy prezentată aici ca un copac (valoare mai mare lăcomie mai mare), o stare de algoritm la valoare: 40, este probabil să ia 29 ca valoare următoare. Mai mult, căutarea sa se încheie la 12. Aceasta se ridică la o valoare de 41.

cu toate acestea, dacă algoritmul a luat o cale sub-optimă sau a adoptat o strategie de cucerire. apoi, 25 ar fi urmat de 40, iar îmbunătățirea generală a costurilor ar fi 65, care este evaluată cu 24 de puncte mai mare ca decizie suboptimă.

Exemple de algoritmi Greedy

majoritatea algoritmilor de rețea folosesc abordarea greedy. Iată o listă cu câteva exemple de algoritmi Greedy:

• minimal Spanning copac algoritm prim lui
• Travelling problema vanzator
• Grafic – harta de colorat
• minimal Spanning copac algoritm Kruskal lui
• minimal Spanning copac algoritm Dijkstra lui
• Grafic – Vertex Cover
• problema rucsacului
• problema programării locurilor de muncă

rezumat:

pentru a rezuma, Articolul a definit paradigma lacom, a arătat cât de optimizare lacom și Recursivitate, vă poate ajuta să obțineți cea mai bună soluție până la un punct. Algoritmul Greedy este luat pe scară largă în aplicare pentru rezolvarea problemelor în multe limbi ca algoritmul Greedy Python, C, C#, PHP, Java, etc. Selecția de activitate a exemplului de algoritm Greedy a fost descrisă ca o problemă strategică care ar putea atinge un randament maxim folosind abordarea greedy. În cele din urmă, au fost explicate dezavantajele utilizării abordării lacome.