Conductivitate termică

conductivitatea termică a solidelor are o natură diferită, în funcție de faptul dacă sunt sau nu conductori. În dielectrice fără sarcini electrice libere, energia termică este transferată de fononi. Vibrațiile colective ale atomilor din rețeaua cristalină iau forma undelor de deplasare, a căror interferență generează pachete de undă, adică fononi. Undele de deplasare produc fluctuații ale densității care se pot manifesta ca o variație a indicelui de refracție. Dacă undele trec printr-o regiune în care indicele de refracție diferă de valoarea volumetrică medie, undele de deplasare ulterioare care transportă energia mișcării termice vor fi împrăștiate.

împrăștierea este mai puternică, cu atât este mai mare abaterea maximă a atomilor de la pozițiile lor medii în rețea, adică cu cât T este mai mare. Acest lucru explică faptul stabilit experimental că conductivitatea termică a dielectricilor cristalini scade la temperaturi destul de ridicate:1/T (Figura 1).

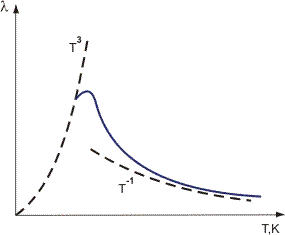
Figura 1. Variația conductivității termice a dielectricilor de cristal cu temperatura.

Debye a oferit o perspectivă asupra unui caracter de vârf al variației de la T la T scăzut în cadrul conceptelor mecanice cuantice. El a elaborat o teorie dipolă a dielectricilor bazată pe conceptul unei molecule ca dipol rigid. În acest model, Debye a introdus conceptul așa-numitei temperaturi Debye, proporțional cu frecvența maximă a vibrațiilor atomice într-un solid. Pentru cele mai multe substanțe, cantitatea de oxid nitric este fie mai mică, fie mai apropiată de temperatura camerei (o excepție este diamantul pentru care cantitatea de oxid nitric = 1850 K și berrylium pentru care cantitatea de oxid nitric = 1160k).

în teoria cuantică a solidelor, rețeaua cristalină este considerată ca un volum umplut cu gaz fonon la care se aplică deducerea celei mai simple teorii cinetice

unde c este capacitatea termică a unui dielectric care coincide cu cea a fononului gazos, v viteza medie a fononilor aproximativ egală cu viteza sunetului,calea medie liberă a fononilor. Existența unei anumite valori finite este rezultatul împrăștierii fononilor pe fononi, pe defectele rețelei cristaline și, în special, pe limitele granulelor pe întregul specimen. Dependența de temperatură(T) este determinată de cea ași c de temperatură.

la temperaturi ridicate care depășesc substanțial temperatura Debye, mecanismul de bază care limitează este o împrăștiere fonon-fonon datorită anarmonicității vibrațiilor atomice dintr-un cristal. Mecanismul fonon-fonon al rezistenței termice ((1 / ZQT) este cunoscut sub numele de coeficient de rezistență termică) este fezabil numai datorită unei tranziții care are ca rezultat întârzierea fluxului fonon și schimbarea apreciabilă a cvasi-impulsului. Cu cât T este mai mare, cu atât este mai mare probabilitatea tranziției cuîn scădere:(1/T). Deoarece la T > capacitatea termică c crește doar ușor cu temperatura, prin urmare, la t1 / T.

la temperaturi mai mici decât temperatura Debye, T<<XVD, lungimea căii libere mediideterminată de împrăștierea fonon-fonon crește drastic,exp XVD/T și, de regulă, este limitată la dimensiunea unui cristal R. conform legii Debye, capacitatea termică c în acest interval de temperatură variază ca c (t/ectod)3. În consecință, la t 0, coeficientul de conductivitate termică a lui T3 trebuie să scadă proporțional cu T3. Temperatura pentru care conductivitatea termică are un vârf este determinată de la xtct R, care corespunde în mod obișnuit t 0,05 xtct.

această teorie explică, de asemenea, comportamentul coeficientului de conductivitate termică pentru substanțele amorfe care nu au o ordine pe distanțe lungi, adică mărimea „cristalelor” lor este de ordinul dimensiunilor atomice. În virtutea acestui fapt, împrăștierea la „limitele” acestor substanțe trebuie să prevaleze la toate T și const. Coeficientul de conductivitate termica a substantelor amorfe, la temperaturi joaseT3, trebuie sa creasca usor, proportional cu capacitatea termica, la temperaturi moderate si inalte, T > T3D.

toate acestea oferă o explicație calitativă a dependenței de dielectrice cristaline reale, dar nu ia în considerare abaterile de la rețeaua constantă datorită impurităților atomice ale altor elemente și ale propriilor izotopi. La o temperatură ridicată, rezistența oferită de impurități la transportul termic este independentă de temperatură. Acest lucru face posibilă estimarea gradului de puritate a cristalului din variația conductivității sale termice cu temperatura. Același fapt ne permite să determinăm distribuția între substanța sticloasă și cristalină în mineralul natural dacă sticla este considerată ca o impuritate într-un cristal.

conductivitatea termică în metale depinde de mișcarea și interacțiunea purtătorilor de curent, adică electronii de conducere. În general, coeficientul de conductivitate termică λ a unui metal este egală cu suma dintre zăbrele (fononice) λph, și electroni λe componente, λ = λe + λph; la temperaturi obisnuite, ca o regulă, λe >>λph.

dacă aplicăm o teorie cinetică simplă a gazelor la fluxul de electroni liberi și presupunem că lungimea căii lor libere nu depinde de viteză, atunci teoria implică faptul că

unde e este sarcina electronilor, constanta lui K Boltzrnann și conductivitatea electrică. O teorie mecanică cuantică strictă oferă o relație similară,

în ambele formule, raportul dintre partea electronică a coeficientului de conductivitate termică la conductivitatea electrică, la un interval larg de temperatură, pare a fi proporțional cu temperatura conform legii Wiedemann-Franz, la fel ca și în cazul L = LT, unde L este numărul Lorentz. Această lege este utilizată pentru a calcula oquste din conductivitatea electrică măsurată. Cu toate acestea, este încălcată la temperaturi sub XVD atunci când predomină o interacțiune electron-fonon (XV crește odată cu scăderea T ca T−5 în timp ce le variază mai ușor ca T−2).

rezultatele experimentale demonstrează că, de regulă, conductivitatea termică a metalelor la temperaturi ridicate este o funcție ușor descrescătoare a temperaturii. Dar există multe excepții. Astfel, conductivitatea termică a fierului scade puternic odată cu temperatura, în timp ce tantalul și niobiul prezintă un coeficient de temperatură pozitiv.

de interes sunt încercările de a compara coeficienții de conductivitate termică pentru diferite substanțe pentru o singură temperatură caracteristică, de exemplu, pentru punctul de topire Tm al solidelor. Astfel, prelucrarea statistică a datelor experimentale efectuate de Missenard a arătat că conductivitatea termică a metalelor la punctul de topire λ(T = Tm) = λm este proporțional cu λși conductivitate termică de dielectrical cristale la T = Tm este în proporție de, unde m este masa moleculară, N numărul de atomi din formula chimică, ρ densitatea, și punctul de topire Tm este, în grade Kelvin.

transportul de căldură în semiconductori este mai complex decât în dielectrici și metale, deoarece fononul și componentele electronice sunt la fel de esențiale pentru ele. Un alt motiv al complexității este efectul considerabil al impurităților, difuziei bipolare și al altor factori puțin studiați asupra transferului de căldură.

efectul presiunii asupra conductivității termice a solidelor poate fi presupus, cu o precizie bună, a fi liniar, cu un nivel minim pentru multe metale care cresc cu p.

pentru efectul porozității asupra conductivității termice a solidelor vezi mediu poros.