am început să fac popular curs de învățare mașină Andrew Ng Pe Coursera. Prima săptămână acoperă foarte mult, cel puțin pentru cineva care nu a atins prea multe calcule de câțiva ani
- funcții de Cost (diferența medie pătrată)
- coborâre Gradient
- regresie liniară
aceste trei subiecte au fost multe de luat. Voi vorbi despre fiecare în detaliu, și modul în care toate se potrivesc împreună, cu unele cod python pentru a demonstra.
Edit 4 mai: Am publicat un follow-up concentrându-se pe modul în care funcționează funcția de Cost aici, inclusiv o intuiție, cum să-l calculeze de mână și două implementări Python diferite. Pot face coborâre gradient și apoi să le aducă împreună pentru regresie liniară în curând.
reprezentarea modelului
în primul rând, scopul majorității algoritmilor de învățare automată este de a construi un model: o ipoteză care poate fi utilizată pentru a estima Y pe baza lui X. ipoteza sau modelul mapează intrările la ieșiri. Deci, de exemplu, să zicem că antrenez un model bazat pe o grămadă de date despre locuințe care include dimensiunea casei și prețul de vânzare. Prin formarea unui model, pot să vă dau o estimare cu privire la cât de mult vă puteți vinde casa ta pentru bazat pe dimensiunea este. Acesta este un exemplu de problemă de regresie — având în vedere unele intrări, dorim să prezicem o ieșire continuă.
ipoteza este de obicei prezentată ca

valorile theta sunt parametrii.
câteva exemple rapide ale modului în care vizualizăm ipoteza:
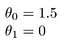
aceasta produce h (x) = 1,5 + 0x. 0x înseamnă nici o pantă, și y va fi întotdeauna Constanta 1.5. Acest lucru arata ca:

ce zici
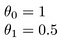

scopul creării unui model este de a alege parametrii sau valorile theta, astfel încât h(x) să fie aproape de y pentru datele de antrenament, x și y. Deci, pentru aceste date
x =
y =

voi încerca și de a găsi o linie de cea mai bună potrivire folosind regresie liniară. Să începem.
funcția Cost
avem nevoie de o funcție care va minimiza parametrii peste setul nostru de date. O funcție comună care este adesea utilizată este eroarea medie pătrată, care măsoară diferența dintre estimator (setul de date) și valoarea estimată (predicția). Se pare ca acest lucru:

se pare că putem ajusta ecuația puțin pentru a face calculul pe pistă puțin mai simplu. Sfârșim cu:
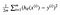
să aplicăm această funcție const la datele de urmărire:

pentru moment, vom calcula unele valori theta, și complot funcția de cost de mână. Deoarece această funcție trece prin (0, 0), ne uităm doar la o singură valoare a theta. De aici încolo, mă voi referi la funcția de cost ca J (XV).
pentru J(1), obținem 0. Nicio surpriză — o valoare de J (1) produce o linie dreaptă care se potrivește perfect datelor. Ce zici de J(0.5)?

funcția MSE ne oferă o valoare de 0,58. Să trasăm ambele valori până acum:
J(1) = 0
J (0,5) = 0.58

voi merge mai departe și să calculeze unele mai multe valori de J(centimetrul).

și dacă ne unim punctele împreună frumos…

putem vedea că funcția de cost este la un nivel minim atunci când theta = 1. Acest lucru are sens — datele noastre inițiale sunt o linie dreaptă cu o pantă de 1 (linia portocalie din figura de mai sus).
Gradient Descent
am minimizat J(XV) prin încercări și erori de mai sus — încercând doar o mulțime de valori și inspectând vizual graficul rezultat. Trebuie să existe o cale mai bună? Coborârea gradientului de coadă. Coborârea gradientului este o funcție generală pentru minimizarea unei funcții, în acest caz funcția medie a costului erorii pătrate.
coborârea gradientului face practic doar ceea ce făceam manual — schimbați valorile theta sau parametrii, puțin câte puțin, până când sperăm că am ajuns la un minim.
începem prin inițializarea theta0 și theta1 la oricare două valori, să zicem 0 pentru ambele și să mergem de acolo. Formal, algoritmul este după cum urmează:

în cazul în care Ecuador, alfa, este rata de învățare, sau cât de repede vrem să se mute spre minim. Cu toate acestea, dacă centimetrul este prea mare, putem depăși.

aducând totul împreună — regresia liniară
rezumând rapid:
avem o ipoteză:

de care avem nevoie pentru a se potrivi cu datele noastre de formare. Putem folosi o funcție de cost astfel de eroare medie pătrat:

pe care o putem minimiza folosind coborârea gradientului:

ceea ce ne conduce la primul nostru algoritm de învățare automată, regresia liniară. Ultima piesă a puzzle-ului pe care trebuie să o rezolvăm pentru a avea un model de regresie liniară funcțională este derivatul parțial al funcției cost:
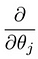
care se dovedește a fi:
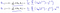
ceea ce ne dă regresie liniară!
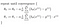
cu teoria din drum, voi continua să pună în aplicare această logică în python în următoarea postare.
Edit 4 Mai: am publicat un follow-up concentrându-se pe modul în care funcția de Cost funcționează aici, inclusiv o intuiție, cum să-l calculeze de mână și două implementări Python diferite. Pot face coborâre gradient și apoi să le aducă împreună pentru regresie liniară în curând.