câmpul electric E poate fi întotdeauna exprimat ca gradient al unei funcții cu potențial scalar
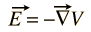
nu există un potențial scalar general pentru câmpul magnetic B, dar poate fi exprimat ca ondularea unei funcții vectoriale
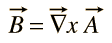
această funcție A primește numele de” potențial vectorial”, dar nu este asociată direct cu munca așa cum este potențialul scalar.
potențialul vectorial este definit ca fiind în concordanță cu Legea lui Ampere și poate fi exprimat în termeni de curent i sau densitate de curent j (sursele câmpului magnetic). În diferite texte această definiție ia formele
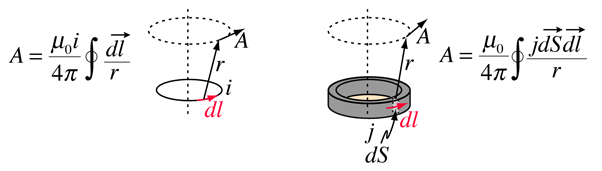
o rațiune pentru potențialul vectorial este că poate fi mai ușor să se calculeze potențialul vectorial decât să se calculeze câmpul magnetic direct dintr-o anumită geometrie a curentului sursă. Aplicația sa cea mai comună este teoria antenei și descrierea undelor electromagnetice.
deoarece câmpul magnetic B este definit ca ondularea lui a, iar prin identitate vectorială ondularea unui gradient este identic zero, atunci orice funcție arbitrară care poate fi exprimată ca gradient al unei funcții scalare poate fi adăugată la A fără a schimba valoarea lui B obținută din ea. Adică, a ‘poate fi înlocuit în mod liber cu A unde
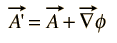
astfel de transformări sunt numite transformări ecartament, și au existat o serie de” calibre”, care au fost folosite pentru a avantaj este tipuri specifice de calcule în teoria electromagnetică.