găsirea unei soluții optime pentru anumite probleme de optimizare poate fi o sarcină incredibil de dificilă, adesea practic imposibilă. Acest lucru se datorează faptului că atunci când o problemă devine suficient de mare, trebuie să căutăm printr-un număr enorm de soluții posibile pentru a găsi cea optimă. Chiar și cu puterea de calcul modernă, există adesea prea multe soluții posibile de luat în considerare. În acest caz, deoarece nu ne putem aștepta în mod realist să o găsim pe cea optimă într-o perioadă sensibilă de timp, trebuie să ne mulțumim cu ceva suficient de aproape.
un exemplu de problemă de optimizare care are de obicei un număr mare de soluții posibile ar fi problema vânzătorului călător. Pentru a găsi o soluție la o problemă, cum ar fi problema vânzătorului călător, trebuie să folosim un algoritm care să poată găsi o soluție suficient de bună într-o perioadă rezonabilă de timp. Într-un tutorial anterior am analizat cum am putea face acest lucru cu algoritmi genetici și, deși algoritmii genetici sunt o modalitate prin care putem găsi o soluție ‘suficient de bună’ la problema vânzătorului călător, există și alți algoritmi mai simpli pe care îi putem implementa, care ne vor găsi și o soluție apropiată de cea optimă. În acest tutorial, algoritmul pe care îl vom folosi este, ‘recoacere simulată’.
dacă nu sunteți familiarizați cu problema comis-voiajor ar putea fi în valoare de a lua o privire la tutorialul meu anterior înainte de a continua.
ce este recoacerea simulată?
în primul rând, să ne uităm la modul în care funcționează recoacerea simulată și de ce este bine să găsim soluții în special la problema vânzătorului călător. Algoritmul de recoacere simulat a fost inițial inspirat din procesul de recoacere în prelucrarea metalelor. Recoacerea implică încălzirea și răcirea unui material pentru a-și modifica proprietățile fizice datorită modificărilor structurii sale interne. Pe măsură ce metalul se răcește, noua sa structură devine fixă, determinând în consecință metalul să-și păstreze proprietățile nou obținute. În recoacerea simulată păstrăm o variabilă de temperatură pentru a simula acest proces de încălzire. Inițial l-am setat ridicat și apoi l-am lăsat să se răcească încet pe măsură ce algoritmul rulează. În timp ce această variabilă de temperatură este ridicată, algoritmul va fi permis, cu mai multă frecvență, să accepte soluții care sunt mai rele decât soluția noastră actuală. Acest lucru oferă algoritmului capacitatea de a sări din orice optimum local pe care îl găsește la începutul execuției. Pe măsură ce temperatura este redusă, la fel este și șansa de a accepta soluții mai proaste, permițând astfel algoritmului să se concentreze treptat pe o zonă a spațiului de căutare în care, sperăm, se poate găsi o soluție apropiată de cea optimă. Acest proces gradual de răcire este ceea ce face ca algoritmul de recoacere simulat să fie remarcabil de eficient în găsirea unei soluții apropiate de cea optimă atunci când se confruntă cu probleme mari care conțin numeroase optimumuri locale. Natura problemei vânzătorului călător îl face un exemplu perfect.
avantajele recoacerii simulate
s-ar putea să vă întrebați dacă există vreun avantaj real în implementarea recoacerii simulate peste ceva de genul unui simplu alpinist de deal. Deși alpiniștii pot fi surprinzător de eficienți în găsirea unei soluții bune, ei au, de asemenea, tendința de a se bloca în optimumurile locale. Așa cum am stabilit anterior, algoritmul de recoacere simulat este excelent pentru a evita această problemă și este mult mai bun în medie la găsirea unui optim global aproximativ.
pentru a vă ajuta să înțelegeți mai bine, să aruncăm rapid o privire la motivul pentru care un algoritm de alpinism de bază este atât de predispus la a fi prins în optimumurile locale.
un algoritm hill climber va accepta pur și simplu soluții vecine care sunt mai bune decât soluția actuală. Când alpinistul nu poate găsi vecini mai buni, se oprește.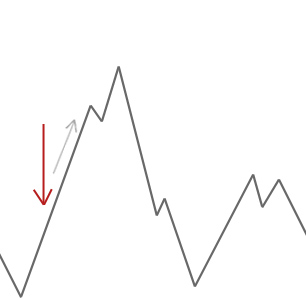
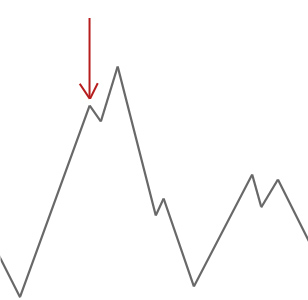
în exemplul de mai sus pornim alpinistul nostru de pe deal la săgeata roșie și își face drum până pe deal până ajunge la un punct în care nu poate urca mai sus fără a coborî mai întâi. În acest exemplu putem vedea clar că este blocat într-un optim local. Dacă aceasta ar fi o problemă reală, nu am ști cum arată spațiul de căutare, așa că, din păcate, nu am putea spune dacă această soluție este aproape de un optim global.
recoacerea simulată funcționează ușor diferit de aceasta și va accepta ocazional soluții mai proaste. Această caracteristică a recoacerii simulate îl ajută să sară din orice optimum local în care altfel s-ar fi putut bloca.
funcția de acceptare
să aruncăm o privire la modul în care algoritmul decide ce soluții să accepte, astfel încât să putem înțelege mai bine modul în care este capabil să evite aceste optimumuri locale.
mai întâi verificăm dacă soluția vecinului este mai bună decât soluția noastră actuală. Dacă este, o acceptăm necondiționat. Dacă totuși, soluția vecinului nu este mai bună, trebuie să luăm în considerare câțiva factori. În primul rând, cât de rău este soluția vecinului; și în al doilea rând, cât de mare este temperatura actuală a sistemului nostru. La temperaturi ridicate sistemul este mult mai probabil să accepte soluții care sunt mai rău.
matematica pentru acest lucru este destul de simplă:
practic, cu cât schimbarea energiei (calitatea soluției) este mai mică și cu cât temperatura este mai mare, cu atât este mai probabil ca algoritmul să accepte soluția.
Prezentare generală a algoritmului
Deci, cum arată algoritmul? Ei bine, în implementarea sa cea mai de bază este destul de simplă.
- mai întâi trebuie să setăm temperatura inițială și să creăm o soluție inițială aleatorie.
- apoi vom începe looping până când starea noastră de oprire este îndeplinită. De obicei, fie Sistemul sa răcit suficient, fie a fost găsită o soluție suficient de bună.
- de aici selectăm un vecin făcând o mică schimbare la soluția noastră actuală.
- apoi decidem dacă să trecem la acea soluție vecină.
- în cele din urmă, scădem temperatura și continuăm bucla
inițializarea temperaturii
pentru o mai bună optimizare, la inițializarea variabilei de temperatură ar trebui să selectăm o temperatură care va permite inițial practic orice mișcare împotriva soluției curente. Acest lucru oferă algoritmului posibilitatea de a explora mai bine întregul spațiu de căutare înainte de a se răci și a se stabili într-o regiune mai concentrată.
exemplu de cod
acum să folosim ceea ce știm pentru a crea un algoritm de recoacere simulat de bază și apoi să îl aplicăm problemei vânzătorului călător de mai jos. Vom folosi Java în acest tutorial, dar logica ar trebui să fie suficient de simplă pentru a copia în orice limbă la alegere.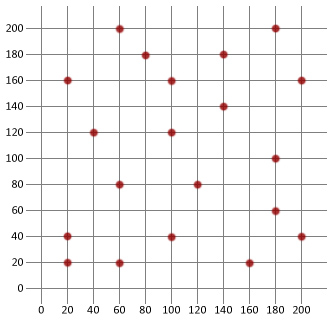
mai întâi trebuie să creăm o clasă de oraș care să poată fi folosită pentru a modela diferitele destinații ale vânzătorului nostru călător.
oraș.java
* oraș.java
* modele un oraș
* /
pachet sa;
public class oraș {
int x;
int y;
/ / construiește un oraș plasat aleatoriu
oraș public () {
acest.x = (Int) (matematică.aleator () * 200);
acest.y = (Int) (Math.random()*200);
}
// construiește un oraș la ales X, Y locație
oraș public(int x, int y) {
aceasta.x = x;
acest.y = y;
}
// devine oraș x coordonate
publice int getX () {
returnați acest lucru.x;
}
// devine Y coordonate orașului
publice int getY(){
returnați acest lucru.y;
}
// devine Distanța până la oraș dat
public double distanceTo(City city) {
int xDistance = Math.abs (getX () – oraș.getX());
int yDistance = matematică . abs (getY () – oraș.getY ());
distanța dublă = matematică.sqrt ((xDistance * xDistance) +(yDistance*yDistance) );
distanța de întoarcere;
}
@Override
public String toString () {
return getX ()+”, ” + getY();
}
}
în continuare, să creăm o clasă care să poată urmări orașele.
TourManager.java
* TourManager.java
* deține orașele unui tur
*/
pachet sa;
import java.util.ArrayList;
public class TourManager {
/ / deține orașele noastre
ArrayList static privat destinationCities = New ArrayList < oraș>();
// adaugă un oraș de destinație
public static void addCity(City city) {
destinationCities.adaugă (oraș);
}
// obțineți un oraș
public static city getCity(int index) {
întoarcere (oraș)destinationCities.obține (index);
}
// obțineți numărul de orașe de destinație
public static int numberOfCities(){
return destinationCities.Dimensiune();
}
}
acum, pentru a crea clasa care poate modela un tur vanzator de călătorie.
tur.java
* tur.java
* stochează un tur candidat prin toate orașele
*/
Pachetul sa;
import java.util.ArrayList;
import java.util.Colecții;
public class Tour {
// deține turul nostru de orașe
private ArrayList tour = New ArrayList<oraș>();
// Cache
distanța int privată = 0;
/ / construiește un tur gol
tur public () {
pentru (int i = 0; i < TourManager.numberOfCities (); i++) {
tur.adaugă(null);
}
}
// construiește un tur dintr-un alt tur
tur public(ArrayList tour){
acest.tur = (ArrayList) tur.clona();
}
// returnează informații tur
public ArrayList getTour () {
tur retur;
}
// creează un individ aleatoriu
public void generateIndividual () {
// buclă prin toate orașele noastre de destinație și adăugați-le la turul nostru
pentru (int cityIndex = 0; cityIndex < TourManager.numberOfCities (); cityIndex++) {
setCity (cityIndex, TourManager.getCity (cityIndex));
}
// reordona aleatoriu tur
colecții.shuffle (tur);
}
// primește un oraș din tur
public city getCity(int tourPosition) {
întoarcere (oraș)tur.obține (tourPosition);
}
// setează un oraș într-o anumită poziție într-un tur
public void setCity(int tourPosition, City city) {
tur.set (tourPosition, oraș);
/ / dacă tururile au fost modificate, trebuie să resetați distanța de fitness și distanța
= 0;
}
// obține distanța totală a turului
public int getDistance () {
if (distance = = 0) {
int tourDistance = 0;
// buclă prin orașele turului nostru
pentru (int cityIndex=0; cityIndex < tourSize(); cityIndex++) {
// Get city călătorim din
City fromCity = getCity(cityIndex);
// City călătorim către
city destinationCity;
// verificați dacă nu suntem în ultimul oraș al turului nostru, dacă suntem setați
// orașul de destinație final al turului către orașul nostru de pornire
dacă(cityIndex+1 < toursize()){
destinationcity = getcity(cityindex+1);
}
else {
destinationCity = getCity(0);
}
// Obțineți distanța dintre cele două orașe
tourDistance += fromCity.distanceTo (destinationCity);
}
distance = tourDistance;
}
distanța de întoarcere;
}
// obțineți numărul de orașe din turul nostru
public int tourSize () {
tur retur.Dimensiune();
}
@suprascrie
public String toString () {
String geneString = „|”;
pentru (int i = 0; i < tourSize (); i++) {
geneString + = getCity (i)+”|”;
}
întoarcere geneString;
}
}
în cele din urmă, să creăm algoritmul nostru de recoacere simulat.
SimulatedAnnealing.java
public class SimulatedAnnealing {
/ / calculați probabilitatea de acceptare
public static double acceptanceProbability (int energy, int newEnergy, double temperature) {
// dacă noua soluție este mai bună, acceptați-o
if (newEnergy < energy) {
return 1.0;
}
// dacă noua soluție este mai rău, se calculează o probabilitate de acceptare
return Math.exp ((energie-newEnergy) / temperatura);
}
publice static void main(string args) {
// creați și adăugați orașele noastre
City city = New City(60, 200);
TourManager.addCity (oraș);
oraș city2 = oraș nou (180, 200);
TourManager.addCity (city2);
oraș city3 = oraș nou(80, 180);
TourManager.addCity(city3);
oraș city4 = oraș nou (140, 180);
TourManager.addCity (city4);
oraș city5 = oraș nou(20, 160);
TourManager.addCity (city5);
oraș city6 = oraș nou(100, 160);
TourManager.addCity (city6);
oraș city7 = oraș nou(200, 160);
TourManager.addCity (city7);
oraș city8 = oraș nou(140, 140);
TourManager.addCity (city8);
oraș city9 = oraș nou(40, 120);
TourManager.addCity (oraș9);
oraș city10 = oraș nou (100, 120);
TourManager.addCity(city10);
oraș city11 = oraș nou (180, 100);
TourManager.addCity(city11);
oraș city12 = oraș nou (60, 80);
TourManager.addCity(city12);
oraș city13 = oraș nou (120, 80);
TourManager.addCity(city13);
oraș city14 = oraș nou (180, 60);
TourManager.addCity(city14);
oraș city15 = oraș nou (20, 40);
TourManager.addCity(city15);
oraș city16 = oraș nou (100, 40);
TourManager.addCity(city16);
oraș city17 = oraș nou (200, 40);
TourManager.addCity (oraș17);
oraș city18 = oraș nou (20, 20);
TourManager.addCity(city18);
oraș city19 = oraș nou (60, 20);
TourManager.addCity(city19);
oraș city20 = oraș nou (160, 20);
TourManager.addCity (city20);
// Set temp inițială
double temp = 10000;
// rata de răcire
double coolingRate = 0.003;
/ / inițializa soluție intial
tour currentSolution = New Tour ();
currentSolution.generateIndividual ();
sistem.afară.println („distanța inițială a soluției:” + currentSolution.getDistance ());
/ / setat ca cel mai bun curent
tur cel mai bun = tur nou(currentSolution.getTour ());
// buclă până când sistemul sa răcit
în timp ce (temp > 1) {
// creați un nou tur vecin
tur newSolution = nou tur(currentSolution.getTour ());
// obțineți o poziție aleatorie în tur
int tourPos1 = (int) (newSolution.tourSize () * Math.aleatoare ());
int tourPos2 = (int) (newSolution.tourSize () * Math.random ());
// Obțineți orașele La pozițiile selectate în tur
oraș citySwap1 = newSolution.getCity (tourPos1);
oraș citySwap2 = newSolution.getCity (tourPos2);
// schimbați-le
newSolution.setCity (tourPos2, citySwap1);
newSolution.setCity (tourPos1, citySwap2);
// obțineți energia soluțiilor
int currentEnergy = currentSolution.getDistance ();
int neighbourEnergy = newSolution.getDistance ();
// Decide dacă ar trebui să acceptăm vecinul
dacă(acceptanceProbability (currentEnergy, neighbourEnergy, temp) > Math.aleatoare ()) {
currentSolution = tur nou (newSolution.getTour());
}
// urmăriți cea mai bună soluție găsită
if (currentSolution.getDistance () < cel mai bun.getDistance ()) {
cel mai bun = tur nou (currentSolution.getTour());
}
// sistem de răcire
temp * = 1-rata de răcire;
}
sistem.afară.println („distanța soluției finale:” + cel mai bun.getDistance ());
sistem.afară.println („tur:” + cel mai bun);
}
}
ieșire
distanța soluției finale: 911
tur: |180, 200/200, 160/140, 140/180, 100/180, 60/200, 40/160, 20/120, 80/100, 40/60, 20/20, 20/20, 40/60, 80/100, 120/40, 120/20, 160/60, 200/80, 180/100, 160/140, 180|
concluzie
în acest exemplu am reușit să mai mult de jumătate din distanța traseului nostru inițial generat aleatoriu. Sperăm că acest lucru va arăta cât de util este acest algoritm relativ simplu atunci când este aplicat anumitor tipuri de probleme de optimizare.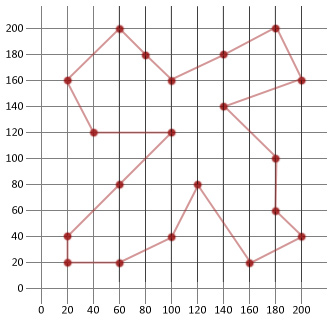
autor
 Bună ziua, Sunt Lee.
Bună ziua, Sunt Lee.sunt un dezvoltator din Marea Britanie care iubește tehnologia și afacerile. Aici veți găsi articole și tutoriale despre lucruri care mă interesează. Dacă vrei să mă angajezi sau să afli mai multe despre mine, mergi la pagina mea despre mine