simplificarea FEA Models: Plane Stress and Plane Strain

Nota editorului: Tony Abbey predă cursuri live NAFEMS FEA în SUA, Europa și Asia. De asemenea, predă cursuri de e-learning NAFEMS la nivel global. Contact .pentru detalii.

un articol anterior de inginerie Desktop („Simplificați modelele de simulare FEA folosind simetria plană”) a explicat că, chiar și cu computerele moderne puternice, există adesea o motivație de a utiliza tehnici de simplificare în analiza elementelor finite structurale (FEA). Această urmărire descrie modul în care două metode strâns legate pot fi utilizate pentru a lua felii 2D printr-o structură complexă în regiunile de interes. Modelele FEA rezultate pot oferi o perspectivă valoroasă asupra tensiunilor locale mai rapid și mai eficient decât un model 3D complet. Nu vor spune întreaga poveste, dar sunt instrumente valoroase pentru inginerul CAE.

cele două metode FEA sunt numite stres plan și tulpina plan. Ambele folosesc elemente plane 2D care arată ca elemente de coajă subțire și sunt ochiuri folosind geometria suprafeței plane.

Analiza Tensiunii Plane

Fig. 1 prezintă faptele importante despre analiza stresului plan. Se presupune că regiunea structurală se află în planul 2D xy, cu a treia dimensiune structurală relativ mică. În figură, aceasta este grosimea în direcția Z. Tensiunile există în planul 2D ca sigma x, sigma y (tensiuni directe) și sigma xy (stres de forfecare în plan). Fiecare dintre aceste tensiuni este constantă prin grosimea așa cum se arată în inserție. În plus, nu poate exista stres în direcția Z. Această relație Material stres-tulpină este definită în elementele de stres plane 2D utilizate în acest tip de analiză.

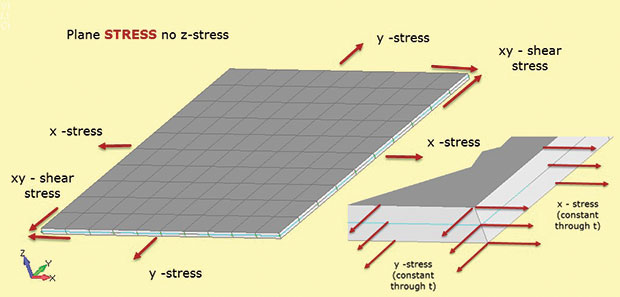Fig. 1: stres plan; ipoteze de stat de stres.

lipsa stresului z este modalitatea de a vă aminti stresul plan de desemnare a tipului de element (adică sunt permise numai solicitările în plan). De asemenea, nu există solicitări de forfecare prin grosime. Am putea încărca modelul de stres plan în Fig. 1 cu o sarcină bi-axială și calculați sigma X și sigma y. nu există sigma z. de asemenea, putem calcula tulpinile corespunzătoare în plan e-x și E-y. dacă aplicăm o sarcină de forfecare, putem găsi stresul de forfecare sigma xy și tulpina de forfecare e-xy. Interesant este că putem calcula și tulpina de grosime e-z. acest lucru nu este zero, deoarece modelul este liber să se subțieze în z pe măsură ce se întinde în x și y. nu există o constrângere în afara planului pentru a preveni acest lucru. În unele solvere putem recupera tulpina de grosime E-z și o putem folosi pentru a calcula modificarea grosimii. (Dacă modelul este în compresie bi-axială, atunci secțiunea z va deveni mai groasă). Aceasta este de obicei considerată o tulpină secundară și poate să nu fie disponibilă pentru ieșire—dar este acolo și poate fi calculată manual, dacă este necesar.

Fig. 2 prezintă o componentă din aluminiu. Lug iese dintr-o foaie compozit layup care a pliuri poziționat și lipite peste tangs (sau picioare) și partea inferioară a corpului. Cârligele transferă sarcina aplicată pe lug în structura compozită. În practică, straturile ar fi pășite pentru a permite un transfer neted de forfecare prin legătură în compozit. Transferul de forfecare în compozit este simulat aici prin forțe de tracțiune difuză de suprafață „trăgând” pe tanguri. Acestea echilibrează sarcina aplicată.

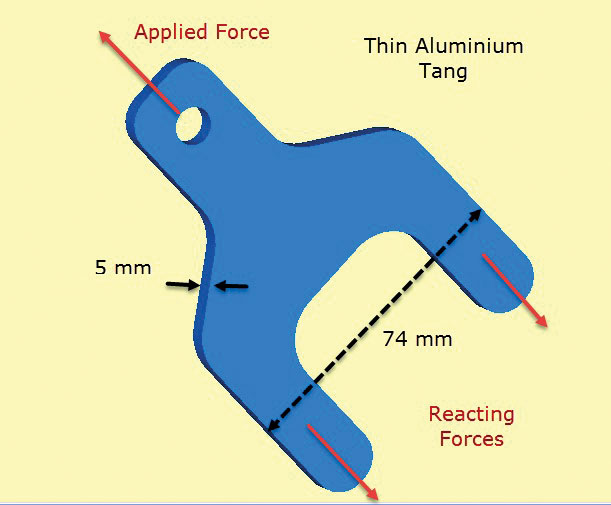Fig. 2: Tang de aluminiu cu pereți subțiri care transferă sarcina în structura compozită.

presupunerea cheie aici este că tensiunile prin grosime sunt zero, iar tensiunile în plan sunt constante prin grosime în componentă. Aceasta înseamnă că detaliile locale ale transferului de sarcină de forfecare de la compozit la tang sunt slab modelate. Cu toate acestea, accentul acestei analize este de a verifica dimensionarea lug și tang secțiune transversală clară a compozitului, folosind tensiuni în plan.

grosimea componentei este mică în comparație cu alte dimensiuni. Această valoare este introdusă ca grosime reală în definiția elementului de stres plan.

Fig. 3 prezintă modelul FEA și tensiunile principale maxime calculate. Zonele de interes sunt în jurul urechilor și a razelor umărului. În lumea reală starea de stres la concentrațiile de stres ar fi 3D și prin grosime Sigma z subliniază și tensiunile de forfecare ar echilibra local. Cu toate acestea, este foarte rezonabil aici să presupunem că tensiunile din plan domină. Aceasta este aceeași presupunere implicită în majoritatea calculelor tradiționale de concentrare a stresului (Kt) găsite în manuale.

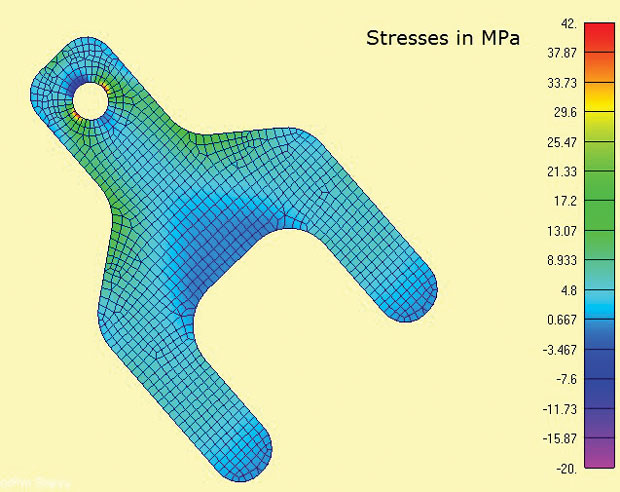Fig 3: elemente de stres plan 2D care prezintă tensiuni principale maxime

una dintre caracteristicile convenabile ale analizei stresului plan este că este o analiză strict 2D, deci trebuie constrânse doar trei grade de libertate (DOF) (traduceri în plan x, y și rotație în jurul axei z). Acest lucru se pretează la metoda de constrângere minimă 3-2-1 cu sarcină echilibrată. Într-un caz 2D acest lucru degenerează la o metodă 2-1. Un nod are DOF x și y constrâns, un al doilea nod ortogonal adecvat are DOF x constrâns. Acest lucru permite ca sarcina de reacție din tanguri să fie aplicată direct ca sarcini de echilibrare difuze. Ar fi dificil să simulăm această condiție de graniță prin constrângeri la sol.

tulpina E-z de grosime și, prin urmare, subțierea tangurilor ar putea fi calculată ca efect secundar.

Analiza Tulpinii Plane

Fig. 4 prezintă esența metodei de deformare plană. Din nou, se folosesc elemente plane 2D, dar cu ipoteze subtil diferite. Tensiunile în plan x, y și xy sunt dezvoltate ca înainte. Cu toate acestea, de data aceasta este out-of-plane, sau prin tulpina grosime z, care este setat la zero. Deci, analiza tulpinii plane permite doar tulpinile în plan. Acest lucru funcționează bine pentru a reprezenta structuri groase, cum ar fi cele prezentate. Prezența acestui material tinde să stabilizeze componenta și să o împiedice să se strecoare în z. acest lucru înseamnă, de asemenea, că în structură se dezvoltă tensiuni constante prin grosime Z. Această relație de material stres-tulpină este definită în elementele de tulpină plană 2D utilizate în acest tip de analiză.

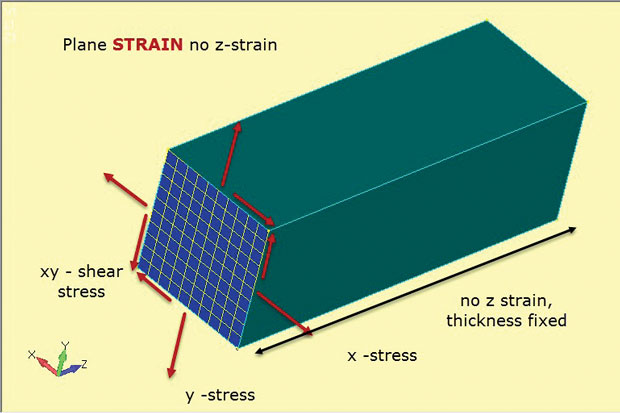Fig. 4: analiza tensiunii Plane; ipoteze de stres și tulpina de stat.

figura prezintă orientarea elementelor de tensionare plană 2D ca secțiune tăiată printr-o componentă tipică profundă. Presupunerea este că starea de stres la această secțiune de tăiere va fi duplicată la orice tăietură plană xy (stația z) prin componentă. Se presupune că componenta este prismatică (având o secțiune transversală constantă) pe lungimea sa.

în practică folosim această metodă în care starea de stres variază încet de la plan la plan într-o componentă profundă. Ar trebui să existe suficient material prin adâncime pentru a stabiliza și elimina tulpina de grosime. Acesta este același principiu utilizat pe specimenele de rezistență la fractură prezentate în Fig. 5. O defecțiune în condiții de tensiune plană este prezentată pentru secțiunea centrală a specimenului gros. Eșecul la marginile libere și secțiunea subțire este un mod diferit, mai mult ca o stare de stres plan. Un model FEA cu tulpină plană ar fi, prin definiție, o bună reprezentare a comportamentului specimenului gros al liniei centrale, dar nu a marginilor libere sau a specimenului subțire.

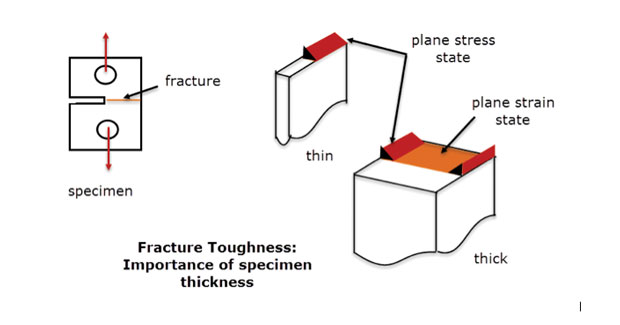Fig. 5: specimene de rezistență la fractură; secțiuni subțiri și groase.

Fig. 6 prezintă o altă componentă utilizată într-o structură compozită, formând o îmbinare lipită. Aici secțiunea este constantă și suficient de adâncă, astfel încât să putem presupune că tensiunile sunt, de asemenea, constante cu adâncimea. Fețele libere ale suprafeței de capăt (at + z, – z) vor avea o stare de stres locală diferită (de fapt stres plan, după cum sa menționat), totuși obiectivul acestei analize este de a verifica tensiunile secțiunii nete de pe linia centrală (z = 0).

plasa de analiză a tensiunii plane 2D este prezentată secționată în componenta 3D în Fig. 7. Secțiunea tăiată este definită la stația z = 0.

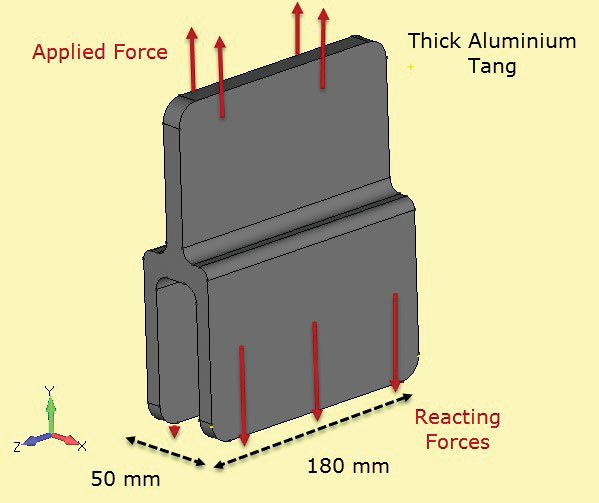Fig 6: tang de aluminiu cu secțiune profundă.

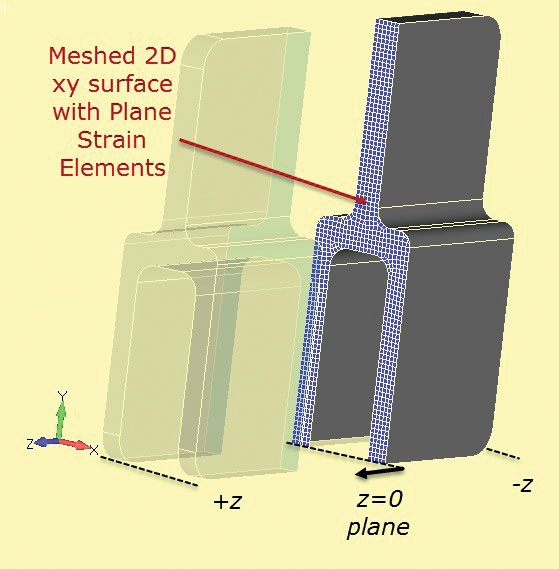Fig. 7: Secțiunea tăiată prin secțiunea solidă pentru a dezvolta secțiunea de tulpină plană 2D.

se poate folosi o plasă de tulpină plană 2D foarte fină, care va rula foarte repede în comparație cu un model 3D complet. Metoda de constrângere 2-1 este utilizată ca înainte. Încărcarea trebuie luată în considerare cu atenție. „Grosimea” secțiunii de tensiune plană este destul de arbitrară și este de obicei setată la 1.0 în mod implicit. Dacă încărcarea pe componentă este calculată ca o sarcină de rulare prin adâncime (N/m, lbf/inch etc.) apoi, această valoare poate fi utilizată direct pe Plasa de tensiune plană. Este util să alegeți o secțiune, cum ar fi tang-ul unic și să estimați tensiunea nominală sau medie din această secțiune pentru componenta completă. Acest lucru poate fi folosit ca o verificare a sănătății în analiza tensiunii plane. Încărcarea incorectă este probabil cauza principală a erorii în această metodă.

rezultatele analizei sunt prezentate în Fig. 8 și arată clar regiunile de stres ridicat în jurul fileului umărului. Tensiunile sunt valabile pentru regiunea centrală de adâncime a componentei (z = 0).

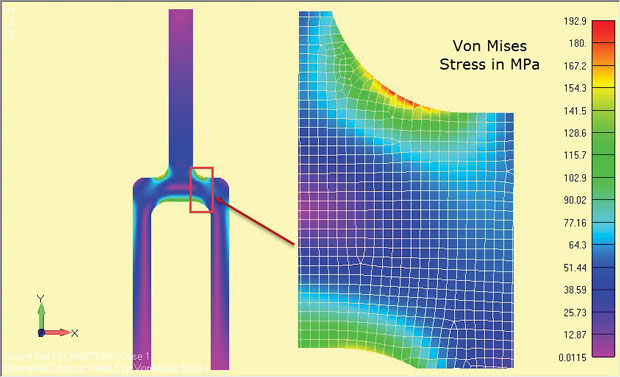Fig. 8: Rezultatele analizei tensiunii Plane a unei componente Tang profunde.

cantitățile de stres utilizate vor depinde de solverul utilizat. Unii rezolvatori ignoră tensiunile de direcție z ca secundare și recuperează tensiunile în plan. Tensiunile principale și tensiunile von Mises se referă apoi la o stare de stres 2D în plan. Dacă stresul de direcție z este recuperat, atunci ar trebui identificat în mod clar, astfel încât starea de stres 2D în plan în planul X-y să poată fi identificată.

ce reprezintă exact stresul Direcției z? Este stresul dezvoltat ca urmare a aplicării tulpinii de direcție zero Z. Stresul acționează ca și cum fețele libere ale secțiunii prismatice ar fi fixate. La planul central al unei componente de secțiune profundă, acestea vor fi tensiunile complementare necesare pentru a menține starea de deformare a direcției z zero. În realitate, pe măsură ce ne îndreptăm spre fețele libere ale suprafeței, stresul z scade la zero și devine o distribuție plană a stresului (așa cum se vede în specimenul mecanicii fracturii groase).

în multe cazuri, cum ar fi un cilindru sub presiune, fețele de capăt sunt acoperite și vor dezvolta de fapt un stres axial datorită forțelor axiale. Acesta va fi un stres diferit de stresul axial indus în analiza tensiunii plane. Va fi necesar un calcul manual pentru a calcula solicitările axiale sau este posibil un model axisimetric suplimentar pentru recipientele sub presiune.

ușurința geometriei și a construcției ochiurilor se pretează bine studiilor „ce-ar fi dacă” sau studiilor mai formale de optimizare a formei.

pentru comparație, s-a realizat o analiză 3D completă pe jumătate de simetrie a componentei deep tang, iar rezultatele sunt prezentate în Fig. 9. Tensiunea nominală pe piciorul Tang superior este identică în ambele cazuri—amintiți-vă că aceasta este baza oricărei verificări a sănătății.

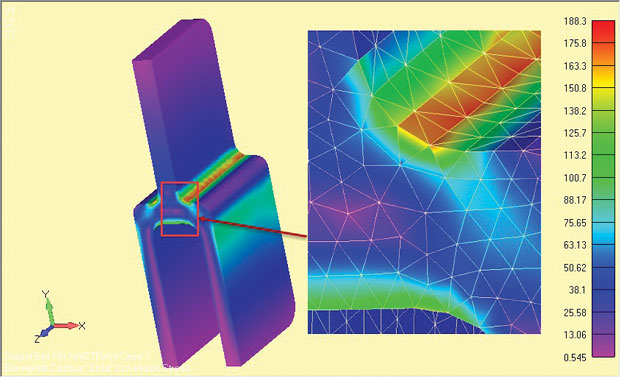Fig. 9: model complet 3D al tang profund, care prezintă rezultate de stres.

tensiunile locale ale umărului sunt mai mici cu un procent mic în modelul complet. Aceasta este din trei motive. În primul rând, plasa TET 3D relativ grosieră este inferioară ochiului de plasă local cu tulpina plană 2D foarte fină. Nu a fost efectuată o verificare a convergenței pe modelul 3d.

în al doilea rând, există o mică modificare a geometriei la suprafețele libere (+z, -z) în comparație cu secțiunea z = 0 datorită fileurilor de capăt. În acest caz, efectul este neglijabil, deoarece fileurile sunt departe de regiunile umărului. În multe componente, cu toate acestea, vor exista fileuri locale, și a alerga afară de detalii. care va varia geometria de la o simplă față plană xy. Variațiile de stres locale la fețele finale libere pot fi estimate sau verificate cu un model 3D complet.

în cele din urmă, presupunerea tulpinii plane a unei constrângeri z fixe la secțiunile +z,-z nu este adevărată pentru o componentă de adâncime finită. Stresul z se va difuza la zero la fețele libere „reale”. Acest efect este prezentat în Fig. 10, care utilizează modelul 3D așa cum este și, de asemenea, ca o simulare a stresului z tulpina planului.

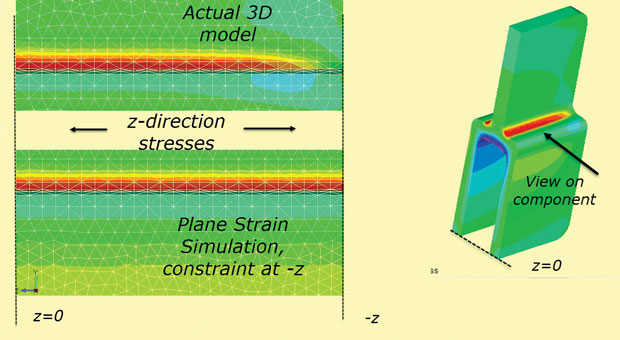Fig. 10: difuzia z-stres spre suprafața liberă.

rapid și eficient

stresul Plane și analizele de tensiune plane sunt metode 2D utile care pot completa adesea modele 3D la scară largă. Nu toate caracteristicile pot fi reprezentate, dar cu o anumită ingeniozitate, stresul în domeniile cheie poate fi cel puțin estimat. Motivația pentru utilizarea metodelor este de a permite o analiză rapidă eficientă, cu o Geometrie 2d ușoară și o construcție a ochiurilor de plasă.